

- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.1 空间几何中的平行(精讲)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.1 空间几何中的平行(精练)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.2 空间几何中的垂直(精练)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.3 空间几何体积及表面积(精讲)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.3 空间几何体积及表面积(精练)(基础版)(原卷版+解析版) 试卷 0 次下载
2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.2 空间几何中的垂直(精讲)(基础版)(原卷版+解析版)
展开考点呈现
例题剖析
考点一 线线垂直
【例1】 (2023·河南)如图,在四棱锥中,底面ABCD为平行四边形,,,,平面平面ABCD.
(1)证明:;
(2)若,E为AD的中点,求三棱锥的体积.
【一隅三反】
1. (2023·北京)如图,在四棱锥中,平面底面,底面为平行四边形,.
(1)求证:;
(2)在棱上是否存在点,使得平面?若存在,指出点的位置;若不存在,请说明理由.
2. (2023·吉林·东北师大附中)如图,四棱锥中,底面ABCD为直角梯形,,,,,为等边三角形,平面平面ABCD.
(1)证明:;
(2)求三棱锥的体积.
3. (2023·四川成都)如图,四棱锥中,四边形为直角梯形,,在底面内的射影分别为,.求证:
考点二 线面垂直
【例2】 (2023·全国·高三专题练习)如图,在四棱锥,底面为梯形,且,,等边三角形所在的平面垂直于底面,.求证:平面;
【一隅三反】
1 (2023·全国·高三专题练习)在四棱锥中,四边形为菱形,,且平面平面.证明:平面;
2. (2023·全国·高三专题练习)在平行四边形中过点作的垂线交的延长线于点,.连接交于点,如图1,将沿折起,使得点到达点的位置.如图2.证明:直线平面.
3. (2023·全国·高三专题练习)如图,四棱锥中,平面平面,为的中点,为的中点,且,,.证明:平面
考点三 面面垂直
【例】 (2023·全国·高三专题练习)在如图1所示的等腰梯形中,,将它沿着两条高折叠成如图2所示的四棱锥(重合),点分别为线段的中点.
(1)证明:平面;
(2)求证:平面平面.
【一隅三反】
1. (2023·四川宜宾)如图,正方形ABED的边长为1,AC=BC,平面ABED⊥平面ABC,直线CE与平面ABC所成角的正切值为.
(1)若G,F分别是EC,BD的中点,求证:平面ABC;
(2)求证:平面BCD⊥平面ACD.
2. (2023·四川成都)如图,三棱锥中,等边三角形的重心为O,,,,E,F,M分别是棱BC,BP,AP的中点,D是线段AM的中点.
(1)求证:平面DEF;
(2)求证:平面平面PBC.
3. (2023·河南·信阳高中)如图所示,直三棱柱中,为中点.
(1)求证:平面;
(2)若三棱柱上下底面为正三角形,,,求证:平面平面.
4. (2023·北京大兴)如图,在四棱锥中,平面,底面为菱形,分别为,的中点.
(1)求证:平面;
(2)求证:平面;
(3)若平面平面,求的大小.
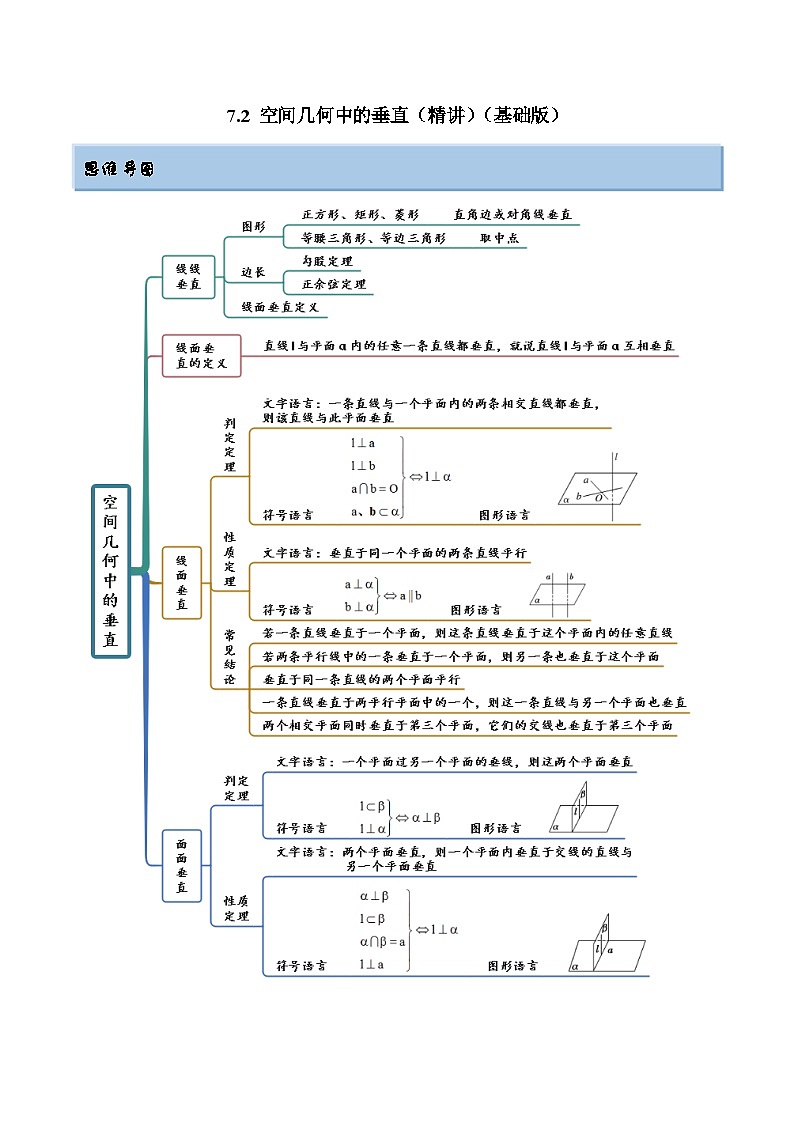
7.2 空间几何中的垂直(精讲)(基础版)
思维导图
考点呈现
例题剖析
考点一 线线垂直
【例1】 (2023·河南)如图,在四棱锥中,底面ABCD为平行四边形,,,,平面平面ABCD.
(1)证明:;
(2)若,E为AD的中点,求三棱锥的体积.
【答案】(1)证明见解析(2)
【解析】(1)证明:在中,由余弦定理,得,
可得,则,即.
又因为平面平面ABCD,且平面平面,
所以平面PAC,
又因为平面PAC,所以.
(2)由(1)可知,而E为AD的中点,故.
又,所以.又,故平面PEC.
又平面PEC,所以.
又,平面ABCD,故平面ABCD.
因为平面ABCD,所以.
因为,故,
在中,,故,
故.
【一隅三反】
1. (2023·北京)如图,在四棱锥中,平面底面,底面为平行四边形,.
(1)求证:;
(2)在棱上是否存在点,使得平面?若存在,指出点的位置;若不存在,请说明理由.
【答案】(1)证明见解析(2)存在,点为棱的中点
【解析】(1)因为平面底面,平面底面,
平面,所以平面.
又因为平面,所以.
(2)解:存在,点为棱的中点.
连接,交于点,连接,如图所示:
因为底面为平行四边形,所以点为的中点.
在中,因为点分别为的中点.
所以,且.
又因为平面平面,所以平面.
2. (2023·吉林·东北师大附中)如图,四棱锥中,底面ABCD为直角梯形,,,,,为等边三角形,平面平面ABCD.
(1)证明:;
(2)求三棱锥的体积.
【答案】(1)证明见解析;(2).
【解析】(1)取中点,连,
因为,,,,
所以四边形为正方形,为等腰直角三角形,则,,
因为面面,面面,面,
所以平面,又平面,所以.
(2)取中点,连,则,且,
因为平面平面,面面,面,
所以平面,又面积为,
三棱锥的体积为.
3. (2023·四川成都)如图,四棱锥中,四边形为直角梯形,,在底面内的射影分别为,.求证:
【答案】证明见解析
【解析】因为在底面内的射影为,所以面面,
又因为,面面,面
所以面,
又因面因此,
同理,
又,面,面
所以面,
又面,所以,
连接,易得,,又,
所以
所以
故,
又,面,面
因此面,
又面
即;
考点二 线面垂直
【例2】 (2023·全国·高三专题练习)如图,在四棱锥,底面为梯形,且,,等边三角形所在的平面垂直于底面,.求证:平面;
【答案】证明见解析
【解析】证明:如图所示,取中点,连接,
是正三角形,为中点,
又平面平面,且平面平面,
平面,
又平面,,
,且,平面,
平面;.
【一隅三反】
1 (2023·全国·高三专题练习)在四棱锥中,四边形为菱形,,且平面平面.证明:平面;
【答案】证明见解析.
【解析】连接BD交AC于O,如图,
四边形为菱形,所以,
平面平面,平面平面平面,
所以平面,因为平面,所以,
,故,
又平面,所以平面.
2. (2023·全国·高三专题练习)在平行四边形中过点作的垂线交的延长线于点,.连接交于点,如图1,将沿折起,使得点到达点的位置.如图2.证明:直线平面.
【答案】证明见解析
【解析】证明:图1中,在中,所以.所以
也是直角三角形,
,
在图2中,所以平面.
3. (2023·全国·高三专题练习)如图,四棱锥中,平面平面,为的中点,为的中点,且,,.证明:平面
【答案】证明见解析
【解析】证明:如图,
连接AF,
由题意知为等腰三角形,
而为的中点,所以.
又因为平面平面,且,平面平面,平面,
所以平面.
而平面,所以.
而,平面,所以平面.
连接,则,,
而,,所以且,
所以是平行四边形,
因此,故平面.
考点三 面面垂直
【例】 (2023·全国·高三专题练习)在如图1所示的等腰梯形中,,将它沿着两条高折叠成如图2所示的四棱锥(重合),点分别为线段的中点.
(1)证明:平面;
(2)求证:平面平面.
【答案】(1)证明见解析(2)证明见解析
【解析】(1)证明:取EC的中点G,连接NG,BG,
因为点分别为线段的中点.所以,
又,所以,所以四边形MBGN是平行四边形,所以,
又平面,平面,所以平面;
(2)证明:因为等腰梯形中,,所以,
所以在中满足,所以,
又,所以平面,所以,
又,所以平面,
又平面,所以平面平面.
【一隅三反】
1. (2023·四川宜宾)如图,正方形ABED的边长为1,AC=BC,平面ABED⊥平面ABC,直线CE与平面ABC所成角的正切值为.
(1)若G,F分别是EC,BD的中点,求证:平面ABC;
(2)求证:平面BCD⊥平面ACD.
【答案】(1)证明见解析;(2)证明见解析.
【解析】(1)如图,连接AE,因F是正方形ABED对角线BD的中点,则F是AE的中点,而G是CE的中点,则,又平面,平面,所以平面.
(2)在正方形中,,因平面ABED⊥平面ABC,平面平面,平面,则平面,即是与平面所成的角,有,解得,即有,则,即,而,则有平面,又平面,于是得,因,平面,则平面,平面,所以平面平面.
2. (2023·四川成都)如图,三棱锥中,等边三角形的重心为O,,,,E,F,M分别是棱BC,BP,AP的中点,D是线段AM的中点.
(1)求证:平面DEF;
(2)求证:平面平面PBC.
【答案】(1)证明见解析(2)证明见解析
【解析】(1)连接PE,因为为等边三角形,且O为重心,所以P、O、E三点共线,且,
因为M为PA中点,D是线段AM的中点,所以,所以,所以,
因为平面DEF,平面DEF,所以平面DEF
(2)连接AE、BD,如图所示
因为为等边三角形,E为BC中点,
所以,
因为,,E为BC中点,
所以,
因为平面PAE,
所以平面PAE,
因为平面PAE,
所以,
在中,,,,
所以,即,
所以,
在中,,
由余弦定理得,
在中,,,
所以,
在中,,,
所以,即,
因为平面PBC,
所以平面PBC,
因为平面DEF,
所以平面平面PBC
3. (2023·河南·信阳高中)如图所示,直三棱柱中,为中点.
(1)求证:平面;
(2)若三棱柱上下底面为正三角形,,,求证:平面平面.
【答案】(1)证明见解析(2)证明见解析
【解析】(1)连接,与相交于点F,连接MF,则为的中点,
因为为中点,所以MF是的中位线,所以,
因为平面,平面,所以平面
(2)因为直三棱柱上下底面为正三角形,,,
所以,
所以,
所以,即,
由三线合一可得:,
又因为平面ABC,平面ABC,
所以,
因为,
所以平面,
因为平面,
所以
因为
所以平面,
因为平面,
所以平面平面
4. (2023·北京大兴)如图,在四棱锥中,平面,底面为菱形,分别为,的中点.
(1)求证:平面;
(2)求证:平面;
(3)若平面平面,求的大小.
【答案】(1)证明见解析(2)证明见解析(3)
【解析】(1)因为平面,平面,所以.
又因为底面为菱形,所以.
又因为,所以平面.
(2)
取为的中点,联结.
在中,分别为的中点,
所以.
因为底面为菱形,且为的中点,
所以.
所以.
所以四边形为平行四边形.
所以.
因为平面平面.
所以平面.
(3)因为平面,平面,所以.
因为平面平面,且平面平面平面,所以平面.
所以.
因为底面为菱形,且为的中点,所以.所以
则是等边三角形.所以.
2024年新高考专用数学第一轮复习讲义一隅三反基础版 4.4 求和方法(精讲)(基础版)(原卷版+解析版): 这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 4.4 求和方法(精讲)(基础版)(原卷版+解析版),共25页。试卷主要包含了裂项相消,错位相减,分组求和,倒序相加等内容,欢迎下载使用。
2024年新高考专用数学第一轮复习讲义一隅三反基础版 4.2 等比数列(精讲)(基础版)(原卷版+解析版): 这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 4.2 等比数列(精讲)(基础版)(原卷版+解析版),共23页。试卷主要包含了等比数列基本量的计算,等比中项,等比数列前n项和的性质,等比数列定义及其运用,等比数列的实际应用等内容,欢迎下载使用。
2024年新高考专用数学第一轮复习讲义一隅三反基础版 4.1 等差数列(精讲)(基础版)(原卷版+解析版): 这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 4.1 等差数列(精讲)(基础版)(原卷版+解析版),共25页。试卷主要包含了等差数列基本量的计算,等差中项,前n项和的性质,等差数列定义及其运用,等差数列的实际应用等内容,欢迎下载使用。












