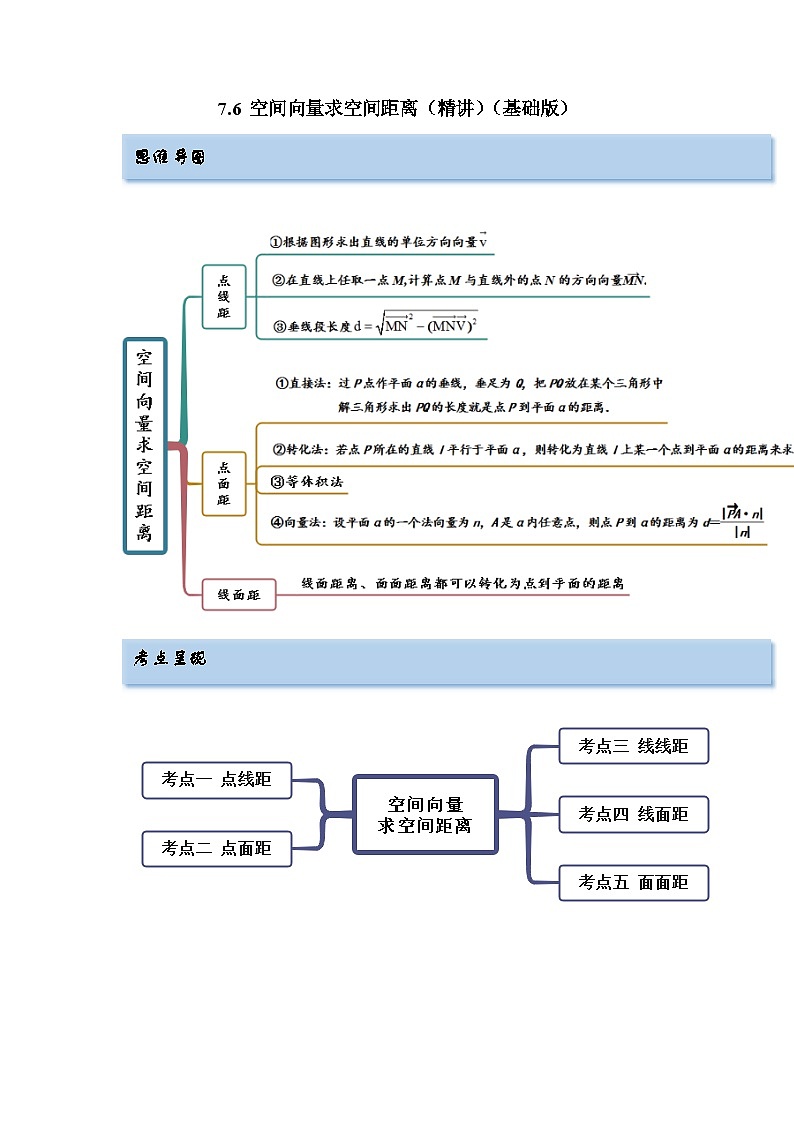
备战2024年高考数学一轮复习(一隅三反基础版新高考专用)7-6 空间向量求空间距离(精讲)(基础版)(原卷版)
展开7.6 空间向量求空间距离(精讲)(基础版)
考点一 点线距
【例1】(2022·福建)在空间直角坐标系中,点,则到直线的距离为___.
【一隅三反】
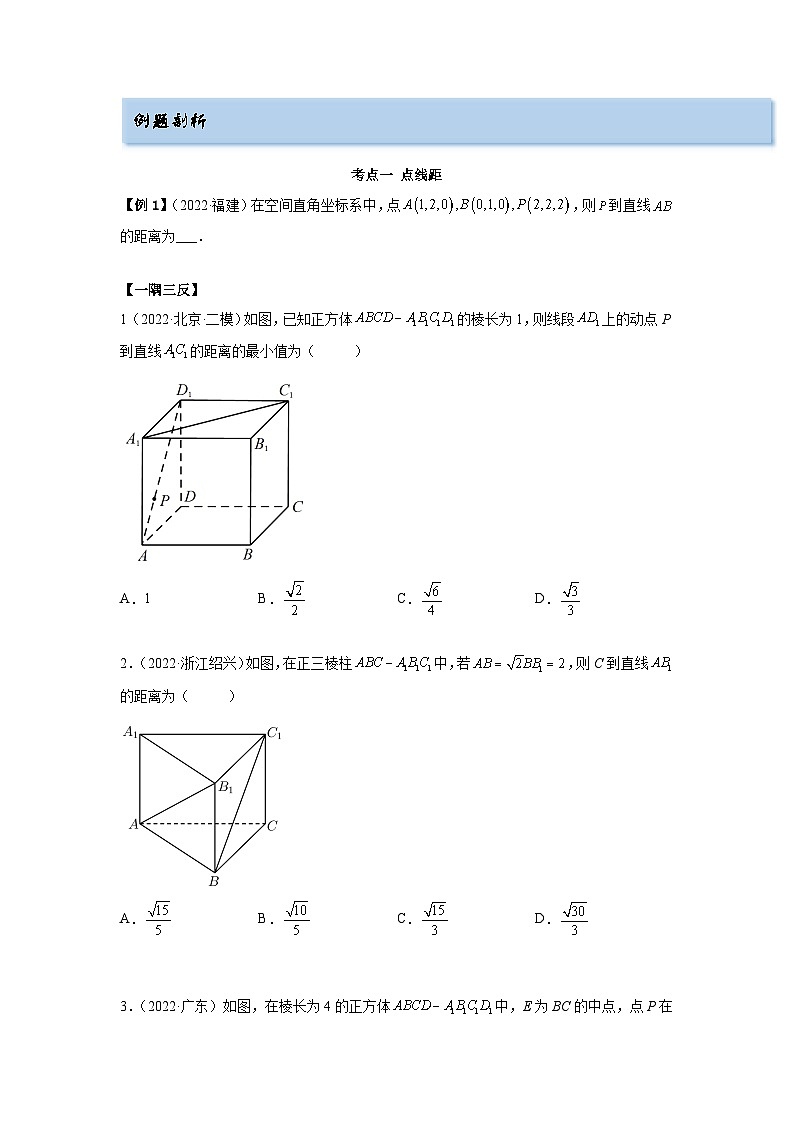
1(2022·北京·二模)如图,已知正方体的棱长为1,则线段上的动点P到直线的距离的最小值为( )
A.1 B. C. D.
2.(2022·浙江绍兴)如图,在正三棱柱中,若,则C到直线的距离为( )
A. B. C. D.
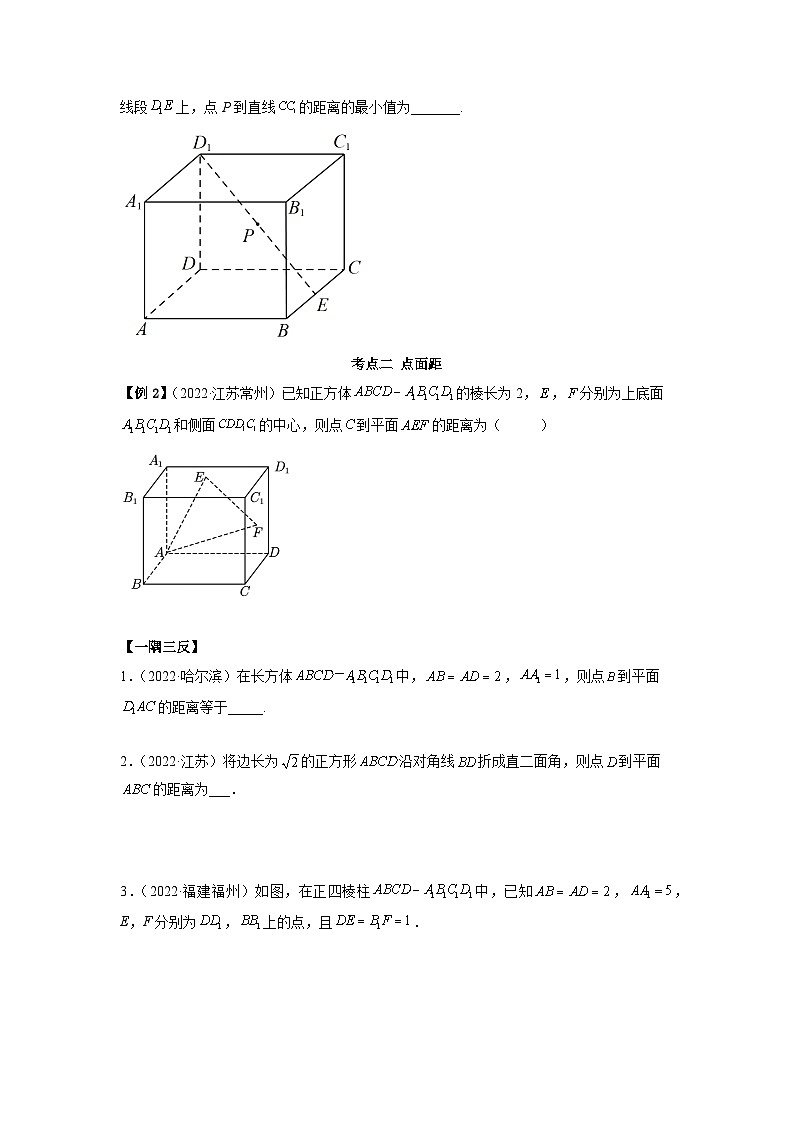
3.(2022·广东)如图,在棱长为4的正方体中,E为BC的中点,点P在线段上,点Р到直线的距离的最小值为_______.
考点二 点面距
【例2】(2022·江苏常州)已知正方体的棱长为2,,分别为上底面和侧面的中心,则点到平面的距离为( )
【一隅三反】
1.(2022·哈尔滨)在长方体中,,,则点到平面的距离等于_____.
2.(2022·江苏)将边长为的正方形沿对角线折成直二面角,则点到平面的距离为___.
3.(2022·福建福州)如图,在正四棱柱中,已知,,E,F分别为,上的点,且.
(1)求证:平面ACF:
(2)求点B到平面ACF的距离.
考点三 线线距
【例3】(2022·全国·高三专题练习)在长方体中,,,,则异面直线与之间的距离是( )
A. B. C. D.
【一隅三反】
1.(2022·山东)定义:两条异面直线之间的距离是指其中一条直线上任意一点到另一条直线距离的最小值.在长方体中,,,,则异面直线与之间的距离是( )
A. B. C. D.
2.(2022·江苏)长方体中,,,为的中点,则异面直线与之间的距离是( )
A. B. C. D.
3.(2022·全国·高三专题练习)定义:两条异面直线之间的距离是指其中一条直线上任意一点到另一条直线距离的最小值.在棱长为1的正方体中,直线与之间的距离是( )
A. B. C. D.
考点四 线面距
【例4】(2022广西)如图,已知斜三棱柱在底面上的射影恰为的中点又知.
(1)求证:平面;
(2)求到平面的距离.
【一隅三反】
1.(2022·山西)如图,在正方体中,为的中点.
(1)证明:平面AD1E
(2)求直线到平面的距离;
2.(2022·海南)如图,在正方体中,棱长为2,为的中点.
(1)求到平面的距离.
(2)若面,求.
3.(2022·北京)图1是直角梯形,四边形是边长为2的菱形,并且,以为折痕将折起,使点到达的位置,且,如图2.
(1)求证:平面平面;
(2)在棱上是否存在点,使得到平面的距离为?若存在,求出直线与平面所成角的正弦值.
考点五 面面距
【例5】(2022·全国·高三专题练习)已知正方体的棱长为a,则平面与平面的距离为( )
A. B. C. D.
【一隅三反】
1.(2022·全国·高三专题练习)在棱长为的正方体中,则平面与平面之间的距离为
A. B.
C. D.
2.(2022山西)两平行平面 , 分别经过坐标原点 和点 ,且两平面的一个法向量 ,则两平面间的距离是 ( )
A. B. C. D.
3.(2022·青海西宁)底面为菱形的直棱柱中,分别为棱的中点.
(1)在图中作一个平面,使得,且平面.(不必给出证明过程,只要求作出与直棱柱的截面).
(2)若,求平面与平面的距离.
2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.6 空间向量求空间距离(精练)(基础版)(原卷版+解析版): 这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.6 空间向量求空间距离(精练)(基础版)(原卷版+解析版),共34页。
2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.6 空间向量求空间距离(精讲)(基础版)(原卷版+解析版): 这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.6 空间向量求空间距离(精讲)(基础版)(原卷版+解析版),共26页。试卷主要包含了点线距,点面距,线线距,线面距,面面距等内容,欢迎下载使用。
2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.5 空间向量求空间角(精讲)(基础版)(原卷版+解析版): 这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.5 空间向量求空间角(精讲)(基础版)(原卷版+解析版),共21页。试卷主要包含了线线角,线面角,二面角等内容,欢迎下载使用。












