【讲通练透】专题08 解三角形-2024高考数学题源解密（全国通用）

这是一份【讲通练透】专题08 解三角形-2024高考数学题源解密（全国通用），文件包含专题08解三角形原卷版docx、专题08解三角形解析版docx等2份试卷配套教学资源，其中试卷共84页， 欢迎下载使用。
高考命题专家命制高考试题时绝非凭空杜撰，必有命题的原始模型（“题根”）和命题着力点（“题眼”），对“题根”与“题眼”进行深入的探求与拓展可构造出高考母题。命题人拿来千变万化为难你们的历年真题，本质上也是从这有限的母题中衍生出来的。母题的重要性不言而喻。
专题08 解三角形
目录一览
2023真题展现
考向一 三角形中的几何运算
考向二 正弦定理
真题考查解读
近年真题对比
考向一 正弦定理
考向二 解三角形
命题规律解密
名校模拟探源
易错易混速记/二级结论速记
考向一 三角形中的几何运算
1．（2023•新高考Ⅱ•第17题）记△ABC的内角A，B，C的对边分别为a，b，c，已知△ABC面积为3，D为BC的中点，且AD＝1．
（1）若∠ADC=π3，求tanB；
（2）若b2+c2＝8，求b，c．
考向二 正弦定理
2．（2023•新高考Ⅰ•第17题）已知在△ABC中，A+B＝3C，2sin（A﹣C）＝sinB．
（1）求sinA；
（2）设AB＝5，求AB边上的高．
【命题意图】
考查正弦定理、余弦定理、三角形面积公式、用正余弦定理解三角形、三角恒等变换等．
【考查要点】
解三角形是高考必考内容．考查正余弦定理和三角形面积公式．借助正余弦定理和三角形面积公式以及恒等变形公式进行边角转换和化简，求边长、角度、面积等．
【得分要点】
1．正弦定理和余弦定理
2．三角形面积公式
（1）S=12a•ha（ha表示边a上的高）．
（2）S=12absinC=12acsinB=12bcsinA．
（3）S=12r（a+b+c）（r为内切圆半径）．
3．解三角形常用结论
考向一 正弦定理
3．（2021•新高考Ⅰ）记△ABC的内角A，B，C的对边分别为a，b，c．已知b2＝ac，点D在边AC上，BDsin∠ABC＝asinC．
（1）证明：BD＝b；
（2）若AD＝2DC，求cs∠ABC．
4．（2021•新高考Ⅱ）在△ABC中，角A，B，C所对的边长为a，b，c，b＝a+1，c＝a+2．
（1）若2sinC＝3sinA，求△ABC的面积；
（2）是否存在正整数a，使得△ABC为钝角三角形？若存在，求出a的值；若不存在，说明理由．
考向二 解三角形
5．（2022•新高考Ⅰ）记△ABC的内角A，B，C的对边分别为a，b，c，已知＝．
（1）若C＝，求B；
（2）求的最小值．
6．（2022•新高考Ⅱ）记△ABC的内角A，B，C的对边分别为a，b，c，分别以a，b，c为边长的三个正三角形的面积依次为S1，S2，S3．已知S1﹣S2+S3＝，sinB＝．
（1）求△ABC的面积；
（2）若sinAsinC＝，求b．
本专题是高考常考内容，结合往年命题规律，解三角形的题目多以解答题的形式出现，分值为10分。
一．正弦定理（共7小题）
1．（2023•淮北二模）已知△ABC的角A，B，C的对边分别为a，b，c，且．
（1）求A；
（2）若△ABC的面积为，sinB＝1+csC，点D为边BC的中点，求AD的长．
2．（2023•西固区校级二模）若△ABC的内角A，B，C的对边分别为a，b，c，满足sin2A﹣sin2B﹣sin2C＝sinBsinC．
（1）求角A；
（2）若a＝6，求△ABC周长的取值范围．
3．（2023•小店区校级模拟）在三角形ABC中，内角A，B，C的对边分别为a，b，c，a＝2b，且．
（1）求角C；
（2）E为三角形ABC所在平面内的一点，且，求线段CE的长．
4．（2023•山西模拟）如图，在四边形ABCD中，已知∠ABC＝，∠BDC＝，AB＝BC＝7．
（1）若BD＝5，求AD的长；
（2）求△ABD面积的最大值．
5．（2023•河南模拟）△ABC的内角A，B，C的对边分别为a，b，c，已知5bsinA＝3atanB，D是AC边上一点，AD＝2DC，BD＝2．
（1）求csB；
（2）求 的最大值．
6．（2023•武昌区校级模拟）已知△ABC的内角A，B，C的对边分别为a，b，c，，BD平分∠ABC交AC于点D，且BD＝2，2AD＝3CD．
（Ⅰ）求B；
（Ⅱ）求△ABC的面积．
7．（2023•润州区校级二模）在①；②；③这三个条件中任选一个，补充在下面的问题中，并解决该问题．
问题：在△ABC中，角A，B，C的对边分别为a，b，c，且满足_____．
（1）求角A的大小；
（2）若D为线段CB延长线上的一点，且，求△ABC的面积．
二．余弦定理（共4小题）
8．（2023•蒙城县校级三模）在△ABC中，∠A，∠B，∠C的对边分别为a，b，c，且cs2C﹣cs2A＝sinAsinB﹣sin2B．
（1）求∠C的大小；
（2）已知a+b＝4，求△ABC的面积的最大值．
9．（2023•广西模拟）在△ABC中，角A，B，C的对边分别为a，b，c．已知．
（1）证明：A＝B．
（2）若D为BC的中点，从①AD＝4，②，③CD＝2这三个条件中选取两个作为条件证明另外一个成立．
注：若选择不同的组合分别解答，则按第一个解答计分．
10．（2023•东风区校级模拟）已知△ABC的内角A，B，C的对应边分别为a，b，c．a＝2，b＝2，且csA（ccsB+bcsC）+asinA＝0．
（1）求A；
（2）设D为BC边上一点，且AD⊥AC，求△ABD的面积．
11．（2023•泸县校级模拟）已知△ABC的角A，B，C的对边分别为a，b，c，满足（b﹣a）（sinB+sinA）＝（b﹣c）sinC．
（1）求A；
（2）从下列条件中：①a＝；②S△ABC＝中任选一个作为已知条件，求△ABC周长的取值范围．
三．三角形中的几何计算（共10小题）
12．（2023•西城区一模）如图，在△ABC中，∠A＝，AC＝，CD平分∠ACB交AB于点D，CD＝．
（Ⅰ）求∠ADC的值；
（Ⅱ）求△BCD的面积．
13．（2023•武功县校级模拟）在△ABC中，是A，B，C所对应的分边别为a，b，c，且满足asinB＝bsin2A．
（1）求∠A；
（2）若a＝2，△ABC的面积为，求三角形的周长．
14．（2023•全国三模）已知a，b，c分别为△ABC的内角A，B，C的对边，且．
（1）求角C；
（2）若c＝2，△ABC的面积为，求△ABC的周长．
15．（2023•船营区校级模拟）在①；②；③这三个条件中任选一个，补充在下面的问题中，并解答问题．
在△ABC中，内角A，B，C的对边分别为a，b，c，且满足____．
（1）求角C；
（2）若△ABC的面积为的中点为D，求BD的最小值．
16．（2023•甘肃模拟）在△ABC中，角A，B，C的对边分别是a，b，c，asin（B+C）＝（b﹣c）sinB+csinC．
（1）求A；
（2）若D在BC上，a＝2，且AD⊥BC，求AD的最大值．
17．（2023•安徽模拟）如图，在Rt△ABC中，AB⊥AC，D，E分别为边CA，CB上一点，．
（1）若，求AB的长；
（2）若∠ADE＝∠BED，求BE的长．
18．（2023•涪城区校级模拟）在①acsB﹣bcsA＝c﹣b，②tanA+tanB+tanC﹣tanBtanC＝0，③△ABC的面积为a（bsinB+csinC﹣asinA），这三个条件中任选一个，补充在下面问题中，并加以解答．
在△ABC中，角A，B，C所对的边分别为a，b，c，且_____．
（1）求角A；
（2）若a＝8，△ABC的内切圆半径为，求△ABC的面积．
19．（2023•邯郸二模）已知条件：①2a＝b+2ccsB；②；③．
从三个条件中任选一个，补充在下面的问题中，并解答．
问题：在△ABC中，角A，B，C所对的边分别为a，b，c，满足：____．
（1）求角C的大小；
（2）若，∠ABC与∠BAC的平分线交于点I，求△ABI周长的最大值．
20．（2023•资阳模拟）在△ABC中，角A，B，C的对边分别为a，b，c，已知bsinB﹣csinC＝a．
（1）证明：
（2）若，，求△ABC的面积．
21．（2023•湖北模拟）如图，在平面四边形ABCD中，AB⊥AD，，AB＝1．
（1）若，求△ABC的面积；
（2）若，，求tan∠CAD．
四．解三角形（共39小题）
22．（2023•凯里市校级一模）在△ABC中，角A、B、C的对边分别为a、b、c，满足sin（B﹣C）＝1，且（bcsC﹣ccsB）tanA＝a．
（1）求A的大小；
（2）若a＝，求△ABC的面积．
23．（2023•沙坪坝区校级模拟）在△ABC中，设角A，B，C所对的边分别为a，b，c，满足＝．
（1）求的值；
（2）若△ABC的面积为1，求边a的最小值．
24．（2023•梅河口市校级模拟）记△ABC的内角A，B，C的对边分别为a，b，c，分别以a，b，c为边长的三个正三角形的面积依次为S1，S2，S3，已知．
（1）求△ABC的面积；
（2）若，求c．
25．（2023•新疆模拟）已知a，b，c分别为△ABC 内角A，B，C的对边，若△ABC 满足cs2A+2sin2＝1，a＝，b＝2．
（1）求角A；
（2）求△ABC的面积．
26．（2023•莆田模拟）△ABC的内角A，B，C的对边分别为a，b，c，已知．
（1）求A；
（2）若，△ABC的面积为，求△ABC的周长．
27．（2023•岳麓区校级模拟）已知△ABC中角A，B，C所对的边分别为a，b，c，且满足2csinAcsB+2bsinAcsC＝a，c＞a．
（1）求角A；
（2）若b＝2，△ABC的面积2，D是BC边上的点，且，求AD．
28．（2023•广陵区校级模拟）如图，四边形ABCD中，已知BC＝1，AC2＝AB2+AB+1．
（1）若△ABC的面积为，求△ABC的周长；
（2）若AB＝3，∠ADB＝60°，∠BCD＝120°，求∠BDC的值．
29．（2023•深圳模拟）已知a、b、c分别为△ABC三内角A、B、C所对的边，且．
（1）求A；
（2）若c2＝4a2﹣4b2，且，求c的值．
30．（2023•桐城市校级二模）已知△ABC满足2sinCsin（B﹣A）＝2sinAsinC﹣sin2B．
（1）试问：角B是否可能为直角？请说明理由；
（2）若△ABC为锐角三角形，求的取值范围．
31．（2023•南京三模）已知＝（sinωx，csωx），＝（csωx，csωx），其中ω＞0，函数f（x）＝•（﹣）的最小正周期为π
（1）求函数f（x）的单调递增区间：
（2）在锐角△ABC中，角A，B，C所对的边分别是a，b，c，且满足f（）＝，求的取值范围．
32．（2023•晋中二模）△ABC的内角A，B，C的对边分别为a，b，c，其中，且满足．
（1）求△ABC的外接圆半径；
（2）若∠B的平分线BD交AC于点D，且，求△ABC的面积．
33．（2023•麒麟区校级模拟）在锐角△ABC中，角A，B，C，的对边分别为a，b，c，从条件①：，条件②：，条件③：2acsA﹣bcsC＝ccsB这三个条件中选择一个作为已知条件．
（1）求角A的大小；
（2）若a＝2，求△ABC周长的取值范围．
34．（2023•龙华区校级模拟）在△ABC中，角A、B、C的对边分别为a、b、c，且满足．
（1）求tanAtanB的值；
（2）若csAcsB＝，c＝6，求△ABC的面积S．
35．（2023•徐州模拟）在△ABC中，角A，B，C所对的边分别为a，b，c，已知b，a，c成等比数列，且．
（1）求B；
（2）若b＝4，延长BC至D，使△ABD的面积为，求sin∠ADC．
36．（2023•保定三模）在△ABC中，BC＝10，，△ABC内有一点M，且BM⊥CM，．
（1）若，求△ABC的面积；
（2）若AC＝14．求BM的长．
37．（2023•招远市模拟）在△ABC中，AB＝4，D为AB中点，．
（1）若BC＝3，求△ABC的面积；
（2）若∠BAC＝2∠ACD，求AC的长．
38．（2023•祁东县校级模拟）如图，在△ABC中，内角A，B，C的对边分别为a，b，c，过点A作AD⊥AB，交线段BC于点D，且AD＝DC，a＝3，bsinC＝asinA﹣bsinB﹣csinC．
（1）求∠BAC；
（2）求△ABC的面积．
39．（2023•定远县校级二模）设函数，若锐角△ABC的内角A，B，C的对边分别为a，b，c，△ABC外接圆的半径为R，acsB﹣bcsA＝R．
（1）若f（A）＝1，求B；
（2）求的取值范围．
40．（2023•乌鲁木齐模拟）在△ABC中，角A，B，C的对边分别为a，b，c，且．
（1）求∠B大小；
（2）若△ABC为锐角三角形，且a＝2，求△ABC面积的取值范围．
41．（2023•青羊区校级模拟）如图，在△ABC中，，点D在AB延长线上，且．
（1）求；
（2）若△ABC面积为，求CD．
42．（2023•朝阳区二模）在△ABC中，a＝4，b＝5，．
（1）求△ABC的面积；
（2）求c及sinA的值．
43．（2023•浙江模拟）在△ABC中，∠A＝90°，点D在BC边上，在平面ABC内，过D作DF⊥BC且DF＝AC．
（1）若D为BC的中点，且△ABC的面积等于△CDF面积的倍，求∠ABC；
（2）若∠ABC＝30°，且CD＝3BD，求tan∠CFB．
44．（2023•陈仓区模拟）记△ABC的内角A，B，C的对边分别为a，b，c，，．
（1）求△ABC的面积；
（2）若，求b．
45．（2023•重庆模拟）在锐角△ABC中，a，b，c分别是△ABC的内角A，B，C所对的边，外接圆周长为，且2（b﹣ccsA）＝a．
（1）求c；
（2）记△ABC的面积为S，求S的取值范围．
46．（2023•青岛二模）在△ABC中，角A，B，C所对的边分别为a，b，c，2a﹣c＝2bcsC．
（1）求B；
（2）若点D为边BC的中点，点E，F分别在边AB，AC上，，b＝c＝2．设∠BDE＝α，将△DEF的面积S表示为α的函数，并求S的取值范围．
47．（2023•威海一模）在△ABC中，角A，B，C所对的边分别为a，b，c，且．
（1）求B；
（2）若a＝3，，求△ABC的面积．
48．（2023•鼓楼区校级模拟）△ABC的内角A，B，C的对边分别为a，b，c，已知，且△ABC的面积．
（1）求C；
（2）若△ABC内一点P满足AP＝AC，BP＝CP，求∠PAC．
49．（2023•沙坪坝区校级模拟）已知△ABC中，角A，B，C的对边分别为a，b，c，．
（1）求A；
（2）若△ABC的面积为，求．
50．（2023•日照一模）已知△ABC中，a，b，c是角A，B，C所对的边，asin＝bsinA，且a＝1．
（1）求B；
（2）若AC＝BC，在△ABC的边AB，AC上分别取D，E两点，使△ADE沿线段DE折叠到平面BCE后，顶点A正好落在边BC（设为点P）上，求此情况下AD的最小值．
51．（2023•香洲区校级模拟）如图所示，在四边形ABCD中，AB＝BC＝CD＝2，AD＝2．
（1）证明csA﹣csC为定值并求出这个定值；
（2）记△ABD 与△BCD的面积分别为S1和S2，求+的最大值．
52．（2023•驻马店二模）在△ABC中，角A，B，C的对边分别是a，b，c，且5cs2B﹣14csB＝7．
（1）求sinB的值；
（2）若a＝5，c＝2，D是线段AC上的一点，求BD的最小值．
53．（2023•乌鲁木齐模拟）在△ABC中，边a，b，c所对的角分别为A，B，C，a＝3，c2＝b2﹣3b+9．
（1）求角C的大小；
（2）若，求边c．
54．（2023•河南模拟）在△ABC中，B≠C，sinB+sinC＝csB+csC．
（1）求A；
（2）若在△ABC内（不包括边界）有一点M，满足CM＝2MA＝2MB，且∠AMC＝90°，求tan∠ACB．
55．（2023•锦江区校级模拟）已知a，b，c分别为锐角△ABC内角A，B，C的对边，c2﹣a2＝ab．
（1）证明：C＝2A；
（2）求的取值范围．
56．（2023•北流市模拟）在△ABC中，角A，B，C所对的边分别a，b，c，且bcsA+acsB＝2ccsA．
（1）求角A的值；
（2）已知D在边BC上，且BD＝3DC，AD＝3，求△ABC的面积的最大值．
57．（2023•湖北模拟）在△ABC中，AB＝9，点D在边BC上，AD＝7．
（1）若，求BD的值，
（2）若，且点D是边BC的中点，求AC的值．
58．（2023•河南模拟）在△ABC中，角A，B，C所对的边分别为a，b，c，且．
（1）求角C；
（2）若c＝4，△ABC的面积为，求a，b．
59．（2023•河北模拟）在△ABC中，角A，B，C的对边分别为a，b，c，且acsAcs（C﹣B）﹣asin2A＝bsinAsinC﹣a．
（1）求A；
（2）已知△ABC的外接圆半径为4，若b+λc有最大值，求实数λ的取值范围．
60．（2023•佛山二模）已知△ABC为锐角三角形，且csA+sinB＝（sinA+csB）．
（1）若C＝，求A；
（2）已知点D在边AC上，且AD＝BD＝2，求CD的取值范围．
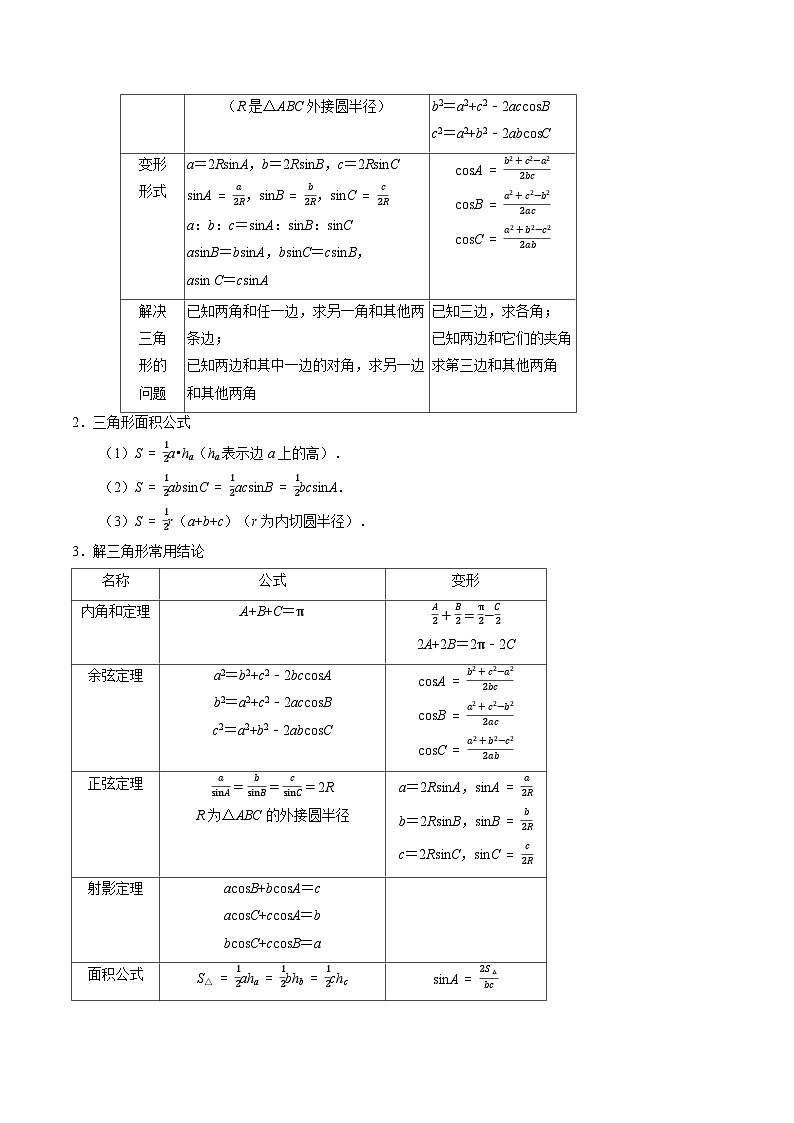
1.正、余弦定理
在△ABC中，若角A，B，C所对的边分别是a，b，c，R为△ABC外接圆半径，则
2.S△ABC＝eq \f(1,2)absin C＝eq \f(1,2)bcsin A＝eq \f(1,2)acsin B＝eq \f(abc,4R)＝eq \f(1,2)(a＋b＋c)·r(r是三角形内切圆的半径)，并可由此计算R，r.
3.在△ABC中，已知a，b和A时，解的情况如下：
定理
正弦定理
余弦定理
内容
asinA=bsinB=csinC=2R
（R是△ABC外接圆半径）
a2＝b2+c2﹣2bccsA
b2＝a2+c2﹣2accsB
c2＝a2+b2﹣2abcsC
变形
形式
a＝2RsinA，b＝2RsinB，c＝2RsinC
sinA=a2R，sinB=b2R，sinC=c2R
a：b：c＝sinA：sinB：sinC
asinB＝bsinA，bsinC＝csinB，
asin C＝csinA
csA=b2+c2−a22bc
csB=a2+c2−b22ac
csC=a2+b2−c22ab
解决
三角
形的
问题
已知两角和任一边，求另一角和其他两条边；
已知两边和其中一边的对角，求另一边和其他两角
已知三边，求各角；
已知两边和它们的夹角求第三边和其他两角
名称
公式
变形
内角和定理
A+B+C＝π
A2+B2=π2−C2
2A+2B＝2π﹣2C
余弦定理
a2＝b2+c2﹣2bccsA
b2＝a2+c2﹣2accsB
c2＝a2+b2﹣2abcsC
csA=b2+c2−a22bc
csB=a2+c2−b22ac
csC=a2+b2−c22ab
正弦定理
asinA=bsinB=csinC=2R
R为△ABC的外接圆半径
a＝2RsinA，sinA=a2R
b＝2RsinB，sinB=b2R
c＝2RsinC，sinC=c2R
射影定理
acsB+bcsA＝c
acsC+ccsA＝b
bcsC+ccsB＝a
面积公式
S△=12aha=12bhb=12chc
S△=12absinC=12acsinB=12bcsinA
S△=12（a+b+c）r
（r为△ABC内切圆半径）
sinA=2S△bc
sinB＝2S△ac
sinC=2S△ab
定理
正弦定理
余弦定理
公式
eq \f(a,sin A)＝eq \f(b,sin B)＝eq \f(c,sin C)＝2R
a2＝b2＋c2－2bccs__A；
b2＝c2＋a2－2cacs__B；
c2＝a2＋b2－2abcs__C
常见变形
(1)a＝2Rsin A，b＝2Rsin__B，c＝2Rsin__C；
(2)sin A＝eq \f(a,2R)，sin B＝eq \f(b,2R)，sin C＝eq \f(c,2R)；
(3)a∶b∶c＝sin__A∶sin__B∶sin__C；
(4)asin B＝bsin A，bsin C＝csin B，asin C＝csin A
cs A＝eq \f(b2＋c2－a2,2bc)；
cs B＝eq \f(c2＋a2－b2,2ac)；
cs C＝eq \f(a2＋b2－c2,2ab)
A为锐角
A为钝角或直角
图形
关系式
a＝bsin A
bsin A