初中数学人教版八年级下册17.1 勾股定理集体备课ppt课件

这是一份初中数学人教版八年级下册17.1 勾股定理集体备课ppt课件，共25页。PPT课件主要包含了带着发现的眼睛，SCSA+SB，c2a2+b2，利用拼图来验证猜想，a2+b2，∴c2a2+b2，赵爽弦图，勾股定理和人类文明，勾股定理的证明，∵S左S右等内容，欢迎下载使用。
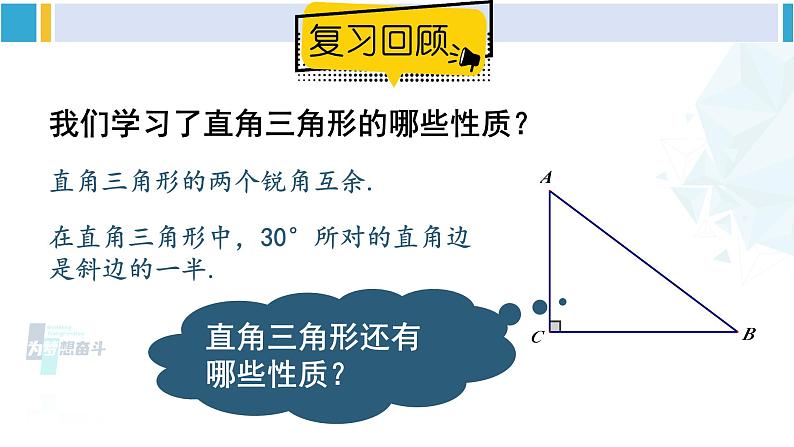
我们学习了直角三角形的哪些性质？
直角三角形的两个锐角互余.
在直角三角形中，30°所对的直角边是斜边的一半.
直角三角形还有哪些性质？
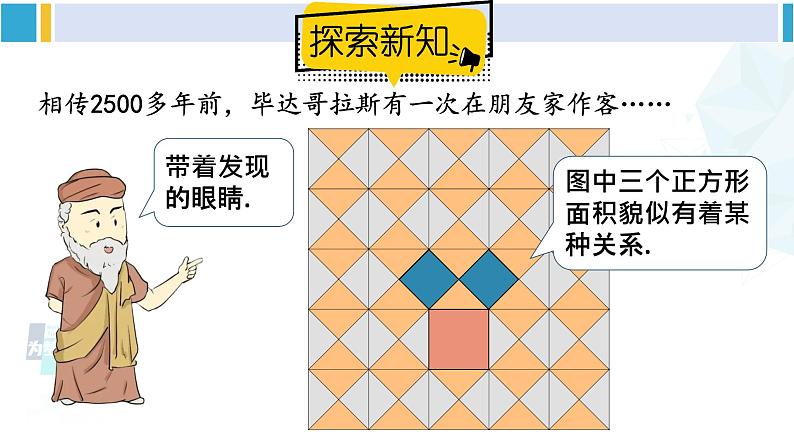
相传2500多年前，毕达哥拉斯有一次在朋友家作客……
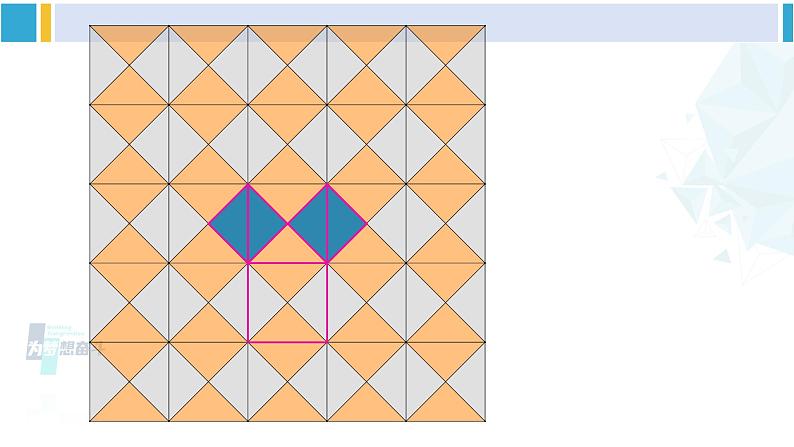
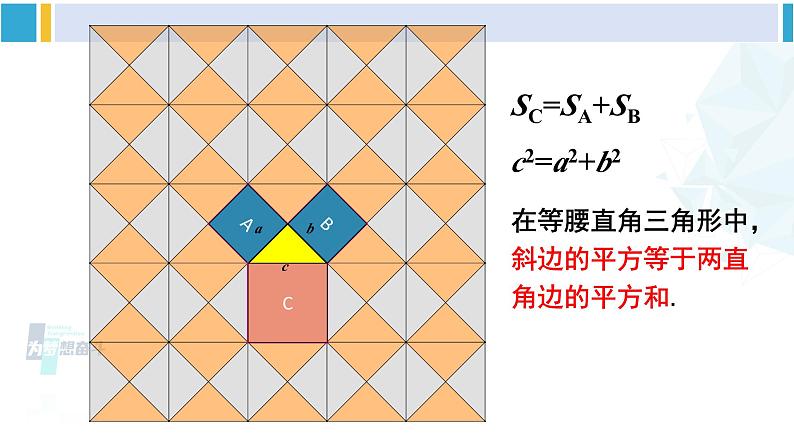
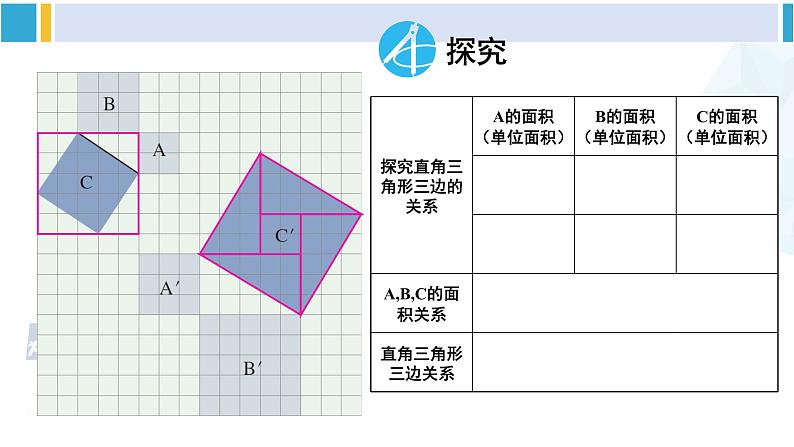
图中三个正方形面积貌似有着某种关系.
在等腰直角三角形中，斜边的平方等于两直角边的平方和.
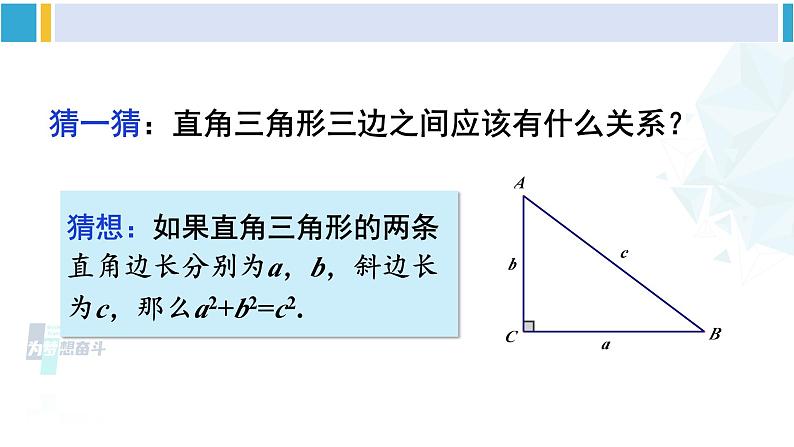
猜一猜：直角三角形三边之间应该有什么关系？
猜想：如果直角三角形的两条直角边长分别为a，b，斜边长为c，那么a2+b2=c2.
1.准备4个全等的直角三角形（设直角三角形的两条直角边分别为a、b，斜边为c）.
2.你能用这四个直角三角形拼成一个以斜边c为边长的正方形吗？拼一拼算算看！
大正方形的面积可以表示为c2.
=2ab+b2-2ab+a2
在中国古代，人们把弯曲成直角的手臂的上半部分称为“勾”，下半部分称为“股”.我国古代把直角三角形中较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.
此结论被称为“勾股定理”.
古希腊数学家毕达哥拉斯，在公元前5世纪给出了这个定理的证明，所以在国外这个定理也称为毕达哥拉斯定理，相传他证出这个定理后非常高兴，宰了一百头牛进行庆祝，于是也有人把它称为“百牛定理”.
如果直角三角形的两条直角边长分别为a，b，斜边长为c，那么a2＋b2=c2.
几何语言：在Rt△ABC中，∠C=90°，∴a2+b2=c2.
我国是最早了解勾股定理的国家之一.早在三千多年前，周朝数学家商高就提出，将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三，股四，弦五”，它被记载于我国古代著名的数学著作《周髀算经》中．在我国勾股定理也叫做“商高定理”.
毕达哥拉斯：利用拼接图形的面积法
题设：Rt△ABC≌Rt△CDE
易证：△ACE为直角三角形，四边形ABDE为梯形
S梯形ABDE=S△ABC+S△CDE+S△ACE
化简得：a2+b2=c2
以直角三角形的勾、股、弦为边，分别作出正方形
勾股定理在数学发展中起到了重大的作用，其证明方法据说有400多种，有兴趣的同学可以继续研究，或到网上查阅勾股定理的相关资料.
1.设直角三角形的两条直角边长分别为a和b，斜边长为c.（1）已知a=6，c=10，求b；（2）已知a=5，b=12，求c；（3）已知c=25，b=15，求a.
【选自教材第24页 练习 第1题】
2.如图所示，已知以直角三角形的三边为边长做3个正方形，求出其中问号正方形的面积.
3.如图，图中所有的三角形都是直角三角形，四边形都是正方形.已知正方形A,B,C,D的边长分别是12，16，9，12，求最大正方形E的面积.
【选自教材第24页 练习 第2题】
解：根据图形正方形E的边长为:
故E的面积为：252=625.
4.求证：S1+S2=S3.
如图，已知长方形ABCD沿直线BD折叠，使点C落在C′处，BC′交AD于E，AD=8，AB=4，求DE的长.
解：∵∠A=∠C′=∠C=90°,∠AEB=∠C′ED，AB=C′D,∴△AEB≌△C′ED.∴AE=C′E,∴C′E=AD-ED=8-ED.又在△EC′D中，ED2=C′E2+C′D2.∴ED2=(8-ED)2+42，解得ED=5.
数学思想：数形结合思想特殊到一般的思想转化思想分类讨论思想