北师大版八年级下册2 图形的旋转精品精练

这是一份北师大版八年级下册2 图形的旋转精品精练，共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.如图，在△ABC中，∠BAC=108°，将△ABC绕点A按逆时针方向旋转得到△AB′C′.若点B′恰好落在BC边上，且AB′=CB′，则∠C′的度数为( )
A. 18°B. 20°C. 24°D. 28°
2.如图，在Rt△ABC中，∠ACB=90°，∠B=60°，BC=1，△A′B′C由△ABC绕点C顺时针旋转得到，其中点A′与点A、点B′与点B是对应点，连接AB′，且A、B′、A′在同一条直线上，则AA′的长为( )
A. 3
B. 2 3
C. 4
D. 4 3
3.如图，在Rt△ABC中，∠C=90°，∠ABC=30°，AC=1cm，将Rt△ABC绕点A逆时针旋转得到Rt△AB′C′，使点C′落在AB边上，连接BB′，则BB′的长度是( )
A. 1cmB. 2cmC. 3cmD. 2 3cm
4.已知点A的坐标为(1,3)，点B的坐标为(2,1).将线段AB沿某一方向平移后，点A的对应点的坐标为(−2,1).则点B的对应点的坐标为( )
A. (5,3)B. (−1,−2)C. (−1,−1)D. (0,−1)
5.如图，在△ABC中，∠A=80°，AC=BC，以点B为旋转中心，把△ABC顺时针旋转α°，得到△A′BC′，点A′恰好落在AC上，连接CC′，则∠ACC′的度数为( )
A. 110°B. 100°C. 90°D. 70°
6.如图，在△ABC中，∠ABC=45°，BC=4，以AC为直角边，点A为直角顶点向△ABC的外侧作等腰直角三角形ACD，连接BD，则△DBC的面积为( )
A. 10
B. 8
C. 4 2
D. 8 2
7.如图，等腰直角三角形ABC，斜边AB=4，D是AB中点，点E为边BC上一动点，直线DE绕点D逆时针旋转90°交AC于点F，则CE+CF的值为( )
A. 2B. 2 3C. 3D. 2 2
8.如图，在△ABC中，将边AB，AC分别绕点A逆时针旋转90°得到线段AD，AE，连接DE，与BC交于点F，连接AF，CD，BE，BD，CE.下列结论：①BC=DE；②BC⊥DE；③AF平分∠BFE；④BE2+CD2=BD2+CE2.其中正确结论的个数为( )
A. 4B. 3C. 2D. 1
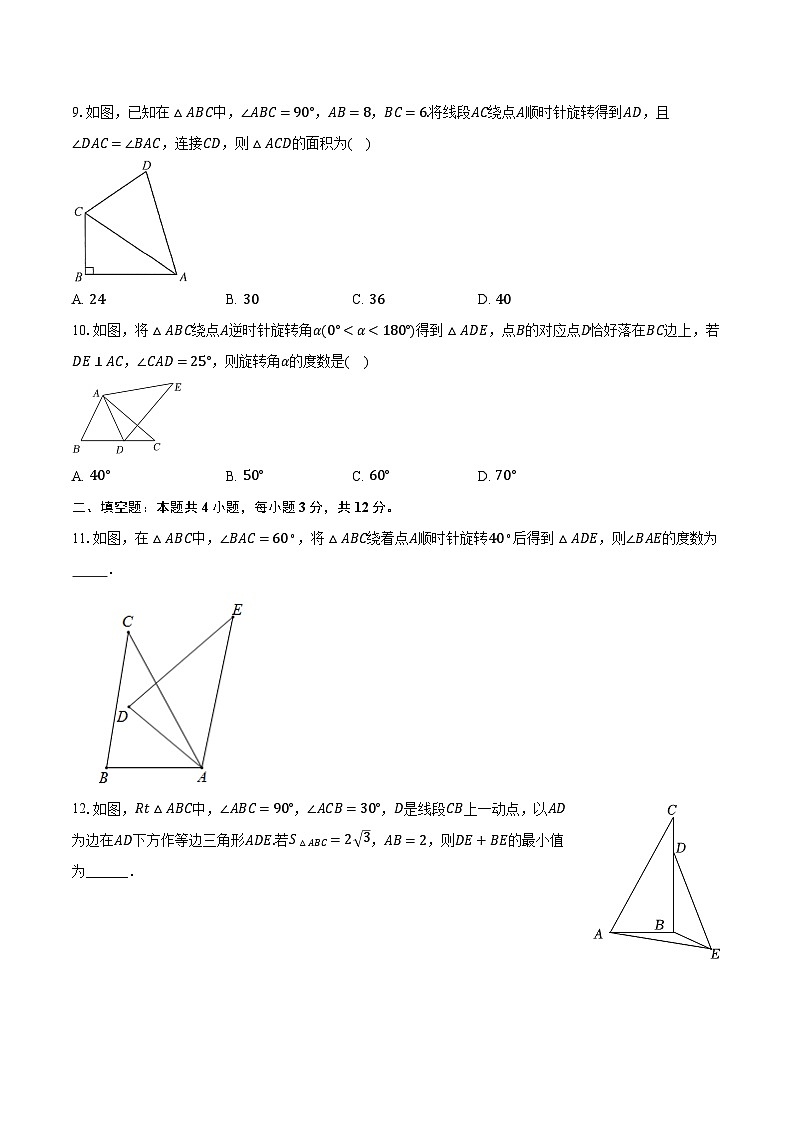
9.如图，已知在△ABC中，∠ABC=90°，AB=8，BC=6.将线段AC绕点A顺时针旋转得到AD，且∠DAC=∠BAC，连接CD，则△ACD的面积为( )
A. 24B. 30C. 36D. 40
10.如图，将△ABC绕点A逆时针旋转角α(0°<α<180°)得到△ADE，点B的对应点D恰好落在BC边上，若DE⊥AC，∠CAD=25°，则旋转角α的度数是( )
A. 40°B. 50°C. 60°D. 70°
二、填空题：本题共4小题，每小题3分，共12分。
11.如图，在△ABC中，∠BAC=60∘，将△ABC绕着点A顺时针旋转40∘后得到△ADE，则∠BAE的度数为 ．
12.如图，Rt△ABC中，∠ABC=90°，∠ACB=30°，D是线段CB上一动点，以AD为边在AD下方作等边三角形ADE.若S△ABC=2 3，AB=2，则DE+BE的最小值为______．
13.如图，在△ABC中，∠C=90∘，AC=4，BC=3，将△ABC绕点A逆时针旋转得到△ADE(点D与点B对应)，连接BD.当点E落在直线AB上时，线段BD的长为 ．
14.如图，等边三角形ABC内有一点P，分别连结AP，BP，CP.若AP=6，BP=8，CP=10，则S△ABP+S△BPC= ．
三、解答题：本题共6小题，共48分。解答应写出文字说明，证明过程或演算步骤。
15.(本小题8分)
如图，△ABC中，点E在BC边上，AE=AB，将线段AC绕A点旋转到AF的位置，使得∠CAF=∠BAE，连接EF，EF与AC交于点G．
(1)求证：EF=BC；
(2)若∠ABC=65°，∠ACB=28°，求∠FGC的度数．
16.(本小题8分)
如图，在等腰三角形ABC中，∠CAB=90°，点P是△ABC内一点，PA=1，PB=3，PC= 7，将△APB绕点A逆时针旋转后与△AQC重合．求：
(1)线段PQ的长；
(2)∠APC的度数
17.(本小题8分)
如图，点O是等边三角形ABC内的一点，∠BOC=150°，将△BOC绕点C按顺时针方向旋转一定的角度，得到△ADC，连接OD，OA．
(1)求∠ODC的度数；
(2)试判断AD与OD的位置关系，并说明理由；
(3)若OB=2，OC=3，求AO的长(直接写出结果)．
18.(本小题8分)
如图，在等腰△ABC中，∠BAC=90°，点D在线段BC的延长线上，连接AD，将线段AD绕点A逆时针旋转90°得到线段AE，连接CE，射线BA与CE相交于点F．
(1)依题意补全图形；
(2)用等式表示线段BD与CE的数量关系，并证明；
(3)若F为CE中点，AB= 2，则CE的长为______．
19.(本小题8分)
将正方形ABCD中的△ABD绕对称中心O旋转至△GEF的位置，EF交AB于点M，GF交BD于点N.请猜想BM与FN有怎样的数量关系？并证明你的结论．
20.(本小题8分)
如图，在边长均为1个单位长度的小正方形组成的网格中，点A，B，O均为格点(每个小正方形的顶点叫做格点)．
(1)作点A关于点O的对称点A1；
(2)连接A1B，将线段A1B绕点A1顺时针旋转90°得到线段A1B1，点B的对应点为B1，画出旋转后的线段A1B1；
(3)连接AB1，BB1，求出△ABB1的面积(直接写出结果即可)．
答案和解析
1.【答案】C
【解析】【分析】本题考查了旋转的性质，等腰三角形的性质，三角形内角和定理，三角形外角的性质，灵活运用这些性质解决问题是本题的关键．
由旋转的性质可得∠C=∠C′，AB=AB′，由等腰三角形的性质可得∠C=∠CAB′，∠B=∠AB′B，由三角形的外角性质和三角形内角和定理可求解．
【解答】
解：∵AB′=CB′，
∴∠C=∠CAB′，
∴∠AB′B=∠C+∠CAB′=2∠C，
∵将△ABC绕点A按逆时针方向旋转得到△AB′C′，
∴∠C=∠C′，AB=AB′，
∴∠B=∠AB′B=2∠C，
∵∠B+∠C+∠CAB=180°，
∴3∠C=180°−108°，
∴∠C=24°，
∴∠C′=∠C=24°，
故选：C．
2.【答案】A
【解析】解：∵∠ACB=90°，∠B=60°，
∴∠BAC=30°，
∴AB=2BC=2×1=2，
∵△ABC绕点C顺时针旋转得到△A′B′C′，
∴A′B′=AB=2，B′C=BC=1，A′C=AC，∠A′=∠BAC=30°，∠A′B′C=∠B=60°，
∴△CAA′为等腰三角形，
∴∠CAA′=∠A′=30°，
∵A、B′、A′在同一条直线上，
∴∠A′B′C=∠B′AC+∠B′CA，
∴∠B′CA=60°−30°=30°，
∴B′A=B′C=1，
∴AA′=AB′+A′B′=2+1=3．
故选：A．
先利用互余计算出∠BAC=30°，再根据含30度的直角三角形三边的关系得到AB=2BC=2，接着根据旋转的性质得A′B′=AB=2，B′C=BC=1，A′C=AC，∠A′=∠BAC=30°，∠A′B′C=∠B=60°，于是可判断△CAA′为等腰三角形，所以∠CAA′=∠A′=30°，再利用三角形外角性质计算出∠B′CA=30°，可得B′A=B′C=1，然后利用AA′=AB′+A′B′进行计算．
本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了含30度的直角三角形三边的关系．
3.【答案】B
【解析】【分析】
本题主要考查了旋转的性质和含30°角的直角三角形，此题实际上是利用直角三角形的性质和旋转的性质将所求线段BB′与已知线段AC的长度联系起来求解的．由直角三角形的性质得到AB=2AC=2，然后根据旋转的性质和等腰三角形的判定得到AB′=BB′．
【解答】
解：∵在Rt△ABC中，∠C=90°，∠ABC=30°，AC=1cm，
∴AC=12AB，则AB=2AC=2cm．
由旋转的性质知，AC′=AC=12AB，B′C′⊥AB，
∴B′C′是AB的中垂线，
∴AB′=BB′．
由旋转的性质知，AB=AB′=BB′=2cm．
故选：B．
4.【答案】C
【解析】【分析】
本题考查了坐标与图形变化−平移，平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减，本题根据对应点的坐标确定出平移规律是解题的关键．
根据点A、点A的对应点的坐标确定出平移规律，然后根据规律求解点B的对应点的坐标即可．
【解答】
解：∵A(1,3)的对应点的坐标为(−2,1)，
∴平移规律为横坐标减3，纵坐标减2，
∴点B(2,1)的对应点的坐标为(−1,−1)．
故选：C．
5.【答案】B
【解析】略
6.【答案】B
【解析】解：∵△ADC是等腰直角三角形，
∴AD=AC，
将△ABC绕着点A逆时针旋转90°得到△AED，
∴△ABC≌△DAE，
∴DE=BC=4，∠ACB=∠ADE，
∵△ADC是等腰直角三角形，
∴∠ADC=∠ACD=45°，
∴∠ADE+∠EDC=45°，
∴∠ACB+∠EDC=45°，
∴∠ACB+∠EDC+∠ACD=90°，
∴∠DEC=90°，
∴DE⊥BC
∴S△BDC=12BC⋅DE=12×4×4=8．
故选：B．
将△ABC绕着点A逆时针旋转90°得到△AED，依据旋转的性质可得DE=BC=4，∠ACB=∠ADE，进而得出∠ACB+∠EDC+∠ACD=90°，然后根据S△BDC=12BC⋅DE求得即可．
本题考查了旋转的性质，等腰直角三角形的性质，正确的作出辅助线是解题的关键．
7.【答案】D
【解析】解：如图，连接CD，
∵△ABC是等腰直角三角形，斜边AB=4，D是AB中点，
∴CD=AD=BD，∠B=∠DCF=45°，BC= 22AB= 22×4=2 2，∠CDB=90°，
由旋转的性质得：∠EDF=90°，
∴∠CDF+∠CDE=90°，
∵∠BDE+∠CDE=∠CDB=90°，
∴∠BDE=∠CDF，
在△BDE和△CDF中，
∠B=∠DCFBD=CD∠BDE=∠CDF，
∴△BDE≌△CDF(ASA)，
∴BE=CF，
∴CE+CF=CE+BE=BC=2 2，
故选：D．
连接CD，先由等腰直角三角形斜边中线性质得CD=AD=BD，∠B=∠DCF=45°，BC= 22AB=2 2，∠CDB=90°，再由旋转的性质得∠EDF=90°，然后证△BDE≌△CDF(ASA)，得出BE=CF，即可得出结果．
本题考查了旋转的性质、等腰直角三角形的性质、全等三角形的判定与性质等性质，正确作出辅助线，构建等腰直角三角形的中线是解题的关键．
8.【答案】A
【解析】解：过A作AM⊥DE于M，AH⊥BC于H，设AC交DE于G，如图：
∵将边AB，AC分别绕点A逆时针旋转90°得到线段AD，AE，
∴∠BAD=∠CAE=90°，AB=AD，AC=AE，
∴∠BAC=∠DAE，
∴△BAC≌△DAE(SAS)，
∴BC=DE，故①正确；
∠BCA=∠DEA，
∵∠CGF=∠EGA，
∴∠CFG=∠EAG=90°，
∴BC⊥DE，故②正确；
∵△BAC≌△DAE，AM⊥DE，AH⊥BC，
∴AM=AH，
∴AF平分∠BFE，故③正确；
∵BC⊥DE，
∴BE2+CD2=BF2+EF2+CF2+DF2，BD2+CE2=BF2+DF2+EF2+CF2，
∴BE2+CD2=BD2+CE2，故④正确；
∴正确的有①②③④，共4个，
故选：A．
过A作AM⊥DE于M，AH⊥BC于H，设AC交DE于G，根据将边AB，AC分别绕点A逆时针旋转90°得到线段AD，AE，可证△BAC≌△DAE(SAS)，得BC=DE，判断①正确；且有∠BCA=∠DEA，而∠CGF=∠EGA，即得∠CFG=∠EAG=90°，BC⊥DE，判断②正确；由△BAC≌△DAE，AM⊥DE，AH⊥BC，可得AM=AH，故AF平分∠BFE，判断③正确；BC⊥DE，根据勾股定理可判断④正确．
本题考查三角形中的旋转问题，涉及全等三角形的判定与旋转，解题的关键是证明△BAC≌△DAE．
9.【答案】B
【解析】过点D作DE⊥AC于点E.在Rt△ABC中，由勾股定理，得AC= AB2+BC2=10.易证△ABC≌△AED，所以DE=BC=6.所以S▵ACD=12AC⋅DE=30．
10.【答案】B
【解析】【分析】
本题考查了旋转的性质，三角形的内角和定理，等腰三角形的性质，解题的关键是熟练掌握旋转的性质进行计算．
先求出∠ADE的度数，然后由旋转的性质和等腰三角形的性质分析求解．
【解答】
解：根据题意，∵DE⊥AC，∠CAD=25°，
∴∠ADE=90°−25°=65°．
由旋转的性质，得∠B=∠ADE=65°，
∵AB=AD，
∴∠ADB=∠B=65°，
∴∠BAD=180°−65°−65°=50°，
∴旋转角α的度数是50°．
故选B．
11.【答案】100°
【解析】【分析】
根据旋转角可得∠CAE=40°，然后根据∠BAE=∠BAC+∠CAE，代入数据进行计算即可得解．
【详解】
解：∵△ABC绕着点A顺时针旋转40°后得到△ADE，∴∠CAE=40°，∵∠BAC=60°，∴∠BAE=∠BAC+∠CAE=60°+40°=100°.故答案为：100°．
【点睛】
本题考查旋转的性质，是基础题，确定出∠CAE=40°是解题关键．
12.【答案】2 3
【解析】解：D在移动的过程中，点E也在运动，则将D点移动到特殊位置上．
D在D′处时，作等边三角形AD′E′，同理作多边形AD′′E′′，连接E′E′′即为E的运动轨迹．
∵DE=AE，
∴DE+BE=AE+BE．
∵∠AE′′E′=90°，
∴过E′′作A的对称点A′，
∵AB=2，且∠A′=30°，
∴A′B=2 3，
∴(AE+BE)min=A′B=2 3．
∴(BE+DE)min=2 3．
故答案为：2 3．
D在移动的过程中，点E也在运动，则将D点移动到特殊位置上，可求出E点运动轨迹．D在D′处时，作等边三角形AD′E′，同理作多边形AD′′E′′，连接E′E′′即为E的运动轨迹．过E′′作A的对称点A′，A′B即为所求．
本题考查了旋转的性质，全等三角形的性质，解题关键在于了解题意，知道点D和点E的运动关系．
13.【答案】 10或 90
【解析】本题易出现的错误是漏解，忽略点E在BA延长线上的情况．
∵∠C=90∘，AC=4，BC=3，
∴AB= AC2+BC2= 42+32=5，
由旋转的性质得∠AED=∠C=90∘，DE=BC=3，AE=AC=4，
如图1，点E在边AB上，则∠DEB=180∘−∠AED=90∘，
∵BE=AB−AE=5−4=1，
∴BD= DE2+BE2= 32+12= 10;
如图2，点E在边BA的延长线上，
∵∠DEB=90∘，BE=AB+AE=5+4=9，
∴BD= DE2+BE2= 32+92= 90．
综上所述，线段BD的长为 10或 90．
14.【答案】24+16 3
【解析】略
15.【答案】解：(1)证明：∵∠CAF=∠BAE，
∴∠BAC=∠EAF．
∵将线段AC绕A点旋转到AF的位置，
∴AC=AF．
在△ABC与△AEF中，
AB=AE∠BAC=∠EAFAC=AF，
∴△ABC≌△AEF(SAS)，
∴EF=BC．
(2)∵AB=AE，∠ABC=65°，
∴∠BAE=180°−65°×2=50°，
∴∠FAG=∠BAE=50°．
∵△ABC≌△AEF，
∴∠F=∠C=28°，
∴∠FGC=∠FAG+∠F=50°+28°=78°．
【解析】本题考查了旋转的性质，全等三角形的判定与性质，等腰三角形的性质，三角形内角和定理以及三角形外角的性质，证明△ABC≌△AEF是解题的关键．
(1)由旋转的性质可得AC=AF，利用SAS证明△ABC≌△AEF，根据全等三角形的对应边相等即可得出EF=BC；
(2)根据等腰三角形的性质以及三角形内角和定理求出∠BAE=180°−65°×2=50°，那么∠FAG=50°.由△ABC≌△AEF，得出∠F=∠C=28°，再根据三角形外角的性质即可求出∠FGC=∠FAG+∠F=78°．
16.【答案】(1)∵△APB绕点A旋转与△AQC重合，
∴AQ=AP=1，
∠QAP=∠CAB=90°．
在Rt△APQ中，由勾股定理得：
PQ= AQ2+AP2 = 12+12 = 2 ．
(2)∵∠QAP=90°，AQ=AP，
∴∠APQ=45°．
∵△APB绕点A旋转与△AQC重合，
∴CQ=BP=3．
∵在△CPQ中，PQ= 2 ，CQ=3，CP= 7
∴CP2+PQ2=( 7 )2+( 2 )2=9，CQ2=32=9．
∴CP2+PQ2=CQ2．
∴∠CPQ=90°．
∴∠APC=∠CPQ+∠APQ=135°．

【解析】见答案
17.【答案】解：(1)由旋转的性质得，CD=CO，∠ACD=∠BCO，
∴∠ACD+∠ACO=∠BCO+∠ACO，即∠DCO=∠ACB，
∵三角形ABC是等边三角形，
∴∠ACB=60°，
∴∠DCO=60°，
∴△OCD为等边三角形，
∴∠ODC=60°；
(2)AD与OD的位置关系是：AD⊥OD，理由如下：
由(1)知∠ODC=60°，
∵将△BOC绕点C按顺时针方向旋转一定的角度，得到△ADC，
∴∠ADC=∠BOC=150°，
∴∠ADO=∠ADC−∠ODC=90°，
∴AD⊥OD；
(3) 13．
【解析】解：(1)见答案；
(2)见答案；
(3)由旋转的性质得，AD=OB=2，
∵△OCD为等边三角形，
∴OD=OC=3，
在Rt△AOD中，由勾股定理得：AO= AD2+OD2= 22+32= 13．
(1)根据旋转的性质得到三角形ODC为等边三角形即可求解；
(2)将△BOC绕点C按顺时针方向旋转一定的角度，得到△ADC，可知∠ADC=∠BOC=150°，即得∠ADO=∠ADC−∠ODC=90°，故AD⊥OD；
(3)在Rt△AOD中，由勾股定理即可求得AO的长．
本题考查等边三角形中的旋转变换，涉及直角三角形判定、勾股定理等知识，解题的关键是掌握旋转的性质，旋转不改变图形的大小和形状．
18.【答案】解：(1)依题意补全图形如下：
(2)线段BD与CE的数量关系是：BD=CE，
证明：在等腰△ABC中，∠BAC=90°，
∴AB=AC，
∵AD绕点A逆时针旋转90°得到AE，
∴AD=AE，∠DAE=90°，
∴∠BAC=∠DAE=90°，
∴∠BAC+∠CAD=∠DAE+∠CAD，
∴∠BAD=∠CAE，
∴△ABD≌△ACE(SAS)，
∴BD=CE；
(3)4．
【解析】此题是几何变换综合题，主要考查了旋转的性质，全等三角形的判定和性质，等腰直角三角形的性质，勾股定理，判断出△ABD≌△ACE是解本题的关键．
【分析】
(1)利用旋转画出AE，连接CE，即可得出图形；
(2)先判断出∠BAD=∠CAE，进而判断出△ABD≌△ACE(SAS)，即可得出结论；
(3)先求出BC，再判断出CF=BC，即可得出答案．
【解答】
解：在等腰△ABC中，∠BAC=90°，
∴∠ABC=∠ACB=45°，
又∵在等腰△ABC中，BC2=AB2+AC2，AB= 2，AB=AC，
∴BC2=2AB2=2× 22=4，
BC=2，
由(2)知，△ABD≌△ACE，
∴∠ABD=∠ACE=45°，
∴∠BCE=90°，
∴∠BFC=90°−∠ABC=45°=∠ABC，
∴CF=BC=2，
∵点F是CE的中点，
∴CE=2CF=4，
故答案为：4．
19.【答案】解：猜想：BM=FN．
证明：在正方形ABCD中，BD为对角线，O为对称中心，
∴BO=DO，∠BDA=∠DBA=45∘，
∵△GEF为△ABD绕O点旋转所得，
∴FO=DO，∠F=∠BDA，
∴OB=OF，∠OBM=∠OFN，
在△OMB和△ONF中，
∠OBM=∠OFNOB=OF∠BOM=∠FON
∴△OBM≌△OFN，
∴BM=FN⋅
【解析】见答案
20.【答案】解：(1)如图所示，点A1即为所求；
(2)如图所示，线段A1B1即为所求；
(3)S△ABB1=8．
【解析】解：(1)见答案；
(2)见答案；
(3)如图，连接AB1，BB1，
则S△ABB1=12×8×2=8．
(1)依据中心对称的性质，即可得到点A关于点O的对称点A1；
(2)依据线段A1B绕点A1顺时针旋转90°得点B的对应点B1，即可得出旋转后的线段A1B1；
(3)依据三角形的面积公式进行计算即可．
本题主要考查了利用旋转变换作图，掌握旋转的性质是解题的关键．