湖北省天门市九校联考2023-2024学年九年级上学期12月月考数学试卷(含答案)

这是一份湖北省天门市九校联考2023-2024学年九年级上学期12月月考数学试卷(含答案)，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

(考试时间：120分钟 试卷总分120分)
一、选择题（每题3分）
1. 关于x的方程x2+4kx+2k2＝4的一个解是﹣2，则k值为（ ）
A．2或4B．0或4C．﹣2或0D．﹣2或2
2. 如图，点A，B，C在⊙O上，若∠C＝55°，则∠AOB的度数为（ ）
A．95°B．100°C．105°D．110°
3. 如图，将△ABC绕点A逆时针旋转55°得到△ADE，若∠E＝70°且AD⊥BC于点F，则∠BAC的度数为（ ）
A．65°B．70°C．75°D．80°
4．掷两枚质地均匀的骰子，下列事件是随机事件的是（ ）
A．点数的和为1B．点数的和为6
C．点数的和大于12D．点数的和小于13
5. 某反比例函数图象上四个点的坐标分别为（﹣3，y1），（﹣2，3），（1，y2），（2，y3），则，y1，y2，y3的大小关系为（ ）
A．y2＜y1＜y3B．y3＜y2＜y1C．y2＜y3＜y1D．y1＜y3＜y2
6. 将二次函数y＝(x－1)2＋2的图像向上平移3个单位，得到的图像对应的函数表达式是（ ）
A．y＝(x＋2)2＋2 B．y＝(x－1)2＋2 C．y＝(x－1)2－1 D．y＝(x－1)2＋5
7. 国家统计局统计数据显示，我国快递业务逐年增加，2017年至2019年我国快递业务收入由5000亿元增加到7500亿元.设我国2017年至2019年快递业务收入的年平均增长率为，则可列方程为( )
A. B. 5 000×2(1+x)=7 500
C. D.
8.如图，正方形四个顶点分别位于两个反比例函数y＝和y＝的图象的四个分支上，则实数n的值为（ ）
A．﹣3B．﹣C．D．3
第9题图
第8题图
第2题图
第3题图
9我国古代天文学确定方向的方法中蕴藏了平行线的作图法．如《淮南子天文训》中记载：“正朝夕：先树一表东方：操一表却去前表十步，以参望日始出北廉．日直入，又树一表于东方，因西方之表，以参望日方入北康，则定东方两表之中与西方之表，则东西也．”如图，用几何语言叙述作图方法：已知直线a和直线外一定点O，过点O作直线与a平行．（1）以O为圆心，单位长为半径作圆，交直线a于点M，N；（2）分别在MO的延长线及ON上取点A，B，使OA＝OB；（3）连接AB，取其中点C，过O，C两点确定直线b，则直线a∥b．按以上作图顺序，若∠MNO＝35°，则∠AOC＝（ ）
A．35°B．30°C．25°D．20°
10．（3分）如图，在平面直角坐标系xOy中，O为坐标原点，抛物线y＝ax2+bx+c（a≠0）的对称轴为x＝1，与x轴的一个交点位于（2，0），（3，0）两点之间．下列结论：
①2a+b＞0；
②bc＜0；
③a＜﹣c；
④若x1，x2为方程ax2+bx+c＝0的两个根，则﹣3＜x1•x2＜0；
其中正确的有（ ）个．
A．1B．2C．3D．4
二、填空题（每题3分）
11.如图，一名学生推铅球，铅球行进高度y（单位：m）与水平距离x（单位：m）之间的关系是y＝﹣（x﹣10）（x+4），则铅球推出的距离OA＝ m．
12．如图，OA是⊙O的半径，BC是⊙O的弦，OA⊥BC于点D，AE是⊙O的切线，AE交OC的延长线于点E．若∠AOC＝45°，BC＝2，则线段AE的长为 ．
13．若实数a、b分别满足a2﹣3a+2＝0，b2﹣3b+2＝0，且a≠b，则+＝ ．
14.如图，点A（2，2）在双曲线y＝（x＞0）上，将直线OA向上平移若干个单位长度交y轴于点B，交双曲线于点C．若BC＝2，则点C的坐标是 ．
15．如图，将面积为7的正方形OABC和面积为9的正方形ODEF分别绕原点O顺时针旋转，使OA，OD落在数轴上，点A，D在数轴上对应的数字分别为a、b，则b﹣a＝ ．
第11题图
第12题图
第14题图
第15题图
三、解答题（共75分）
16. （6分）设一元二次方程x2+bx+c＝0．在下面的四组条件中选择其中一组b，c的值，使这个方程有两个不相等的实数根，并解这个方程．
①b＝2，c＝1；②b＝3，c＝1；③b＝3，c＝﹣1；④b＝2，c＝2．
注：如果选择多组条件分别作答，按第一个解答计分．
17. （6分）如图，已知∠APB，点M是PB上的一个定点．
（1）尺规作图：请在图1中作⊙O，使得⊙O与射线PB相切于点M，同时与PA相切，切点记为N；
（2）在（1）的条件下，若∠APB＝60°，PM＝3，则所作的⊙O的半径是 ．
18. （6分）天门是个好地方，有着丰富的旅游资源．某天甲、乙两人来天门旅游，两人分别从A、B、C三个景点中随机选择一个景点游览．
（1）甲选择A景点的概率为 ；
（2）请用画树状图或列表的方法，求甲、乙两人中至少有一人选择C景点的概率．
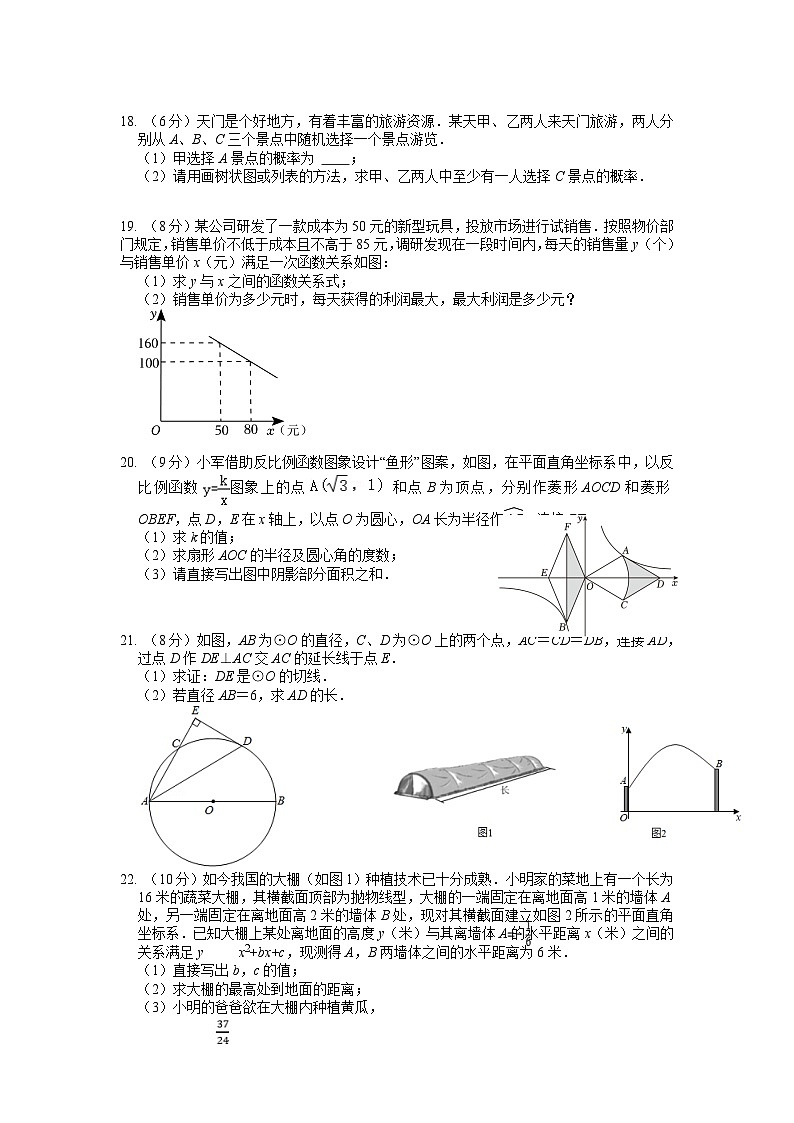
19. （8分）某公司研发了一款成本为50元的新型玩具，投放市场进行试销售．按照物价部门规定，销售单价不低于成本且不高于85元，调研发现在一段时间内，每天的销售量y（个）与销售单价x（元）满足一次函数关系如图：
（1）求y与x之间的函数关系式；
（2）销售单价为多少元时，每天获得的利润最大，最大利润是多少元？
20. （9分）小军借助反比例函数图象设计“鱼形”图案，如图，在平面直角坐标系中，以反比例函数图象上的点 和点B为顶点，分别作菱形AOCD和菱形OBEF，点D，E在x轴上，以点O为圆心，OA长为半径作，连接BF．
​（1）求k的值；
（2）求扇形AOC的半径及圆心角的度数；
（3）请直接写出图中阴影部分面积之和．
21. （8分）如图，AB为⊙O的直径，C、D为⊙O上的两个点， EQ \\ac(\S\UP7(⌒),AC)＝ EQ \\ac(\S\UP7(⌒),CD)＝ EQ \\ac(\S\UP7(⌒),DB)，连接AD，过点D作DE⊥AC交AC的延长线于点E．
（1）求证：DE是⊙O的切线．
（2）若直径AB＝6，求AD的长．
22. （10分）如今我国的大棚（如图1）种植技术已十分成熟．小明家的菜地上有一个长为16米的蔬菜大棚，其横截面顶部为抛物线型，大棚的一端固定在离地面高1米的墙体A处，另一端固定在离地面高2米的墙体B处，现对其横截面建立如图2所示的平面直角坐标系．已知大棚上某处离地面的高度y（米）与其离墙体A的水平距离x（米）之间的关系满足y x2+bx+c，现测得A，B两墙体之间的水平距离为6米．
（1）直接写出b，c的值；
（2）求大棚的最高处到地面的距离；
（3）小明的爸爸欲在大棚内种植黄瓜，
需搭建高为 米的竹竿支架若干，已知大棚内可以搭建支架的土地平均每平方米需要4根竹竿，则共需要准备多少根竹竿？
23. （10分）【探究与证明】如图①，小红在学习了三角形相关知识后，对等腰直角三角形进行了探究，在等腰直角三角形ABC中，CA＝CB，∠C＝90°，过点B作射线BD⊥AB，垂足为B，点P在CB上．
（1）【动手操作】
如图②，若点P在线段CB上，画出射线PA，并将射线PA绕点P逆时针旋转90°与BD交于点E，根据题意在图中画出图形，图中∠PBE的度数为 度；
（2）【问题探究】
根据（1）所画图形，探究线段PA与PE的数量关系，并说明理由；
（3）【拓展延伸】
如图③，若点P在射线CB上移动，将射线PA绕点P逆时针旋转90°与BD交于点E，探究线段BA，BP，BE之间的数量关系，并说明理由．
24. （12分）【问题背景】“刻漏”是我国古代的一种利用水流计时的工具．综合实践小组准备用甲、乙两个透明的竖直放置的容器和一根带节流阀（控制水的流速大小）的软管制作简易计时装置．
【实验操作】综合实践小组设计了如下的实验：先在甲容器里加满水，此时水面高度为30cm，开始放水后每隔10min观察一次甲容器中的水面高度，获得的数据如表：
任务1：分别计算表中每隔10min水面高度观察值的变化量．
【建立模型】小组讨论发现：“t＝0，h＝30”是初始状态下的准确数据，水面高度值的变化不均匀，但可以用一次函数近似地刻画水面高度h与流水时间t的关系．
任务2：利用t＝0时，h＝30；t＝10时，h＝29这两组数据求水面高度h与流水时间t的函数解析式；
【反思优化】经检验，发现有两组表中观察值不满足任务2中求出的函数解析式，存在偏差，小组决定优化函数解析式，减少偏差．通过查阅资料后知道：t为表中数据时，根据解析式求出所对应的函数值，计算这些函数值与对应h的观察值之差的平方和，记为w；w越小，偏差越小．
任务3：（1）计算任务2得到的函数解析式的w值；
（2）请确定经过（0，30）的一次函数解析式，使得w的值最小；
【设计刻度】得到优化的函数解析式后，综合实践小组决定在甲容器外壁设计刻度，通过刻度直接读取时间．
任务4：请你简要写出时间刻度的设计方案．
数学参考答案
选择题（每题3分）
BDCBC DCAAB
填空题（每题3分）
11.10 12. 13. 14.（，2） 15.
三、解答题
16.（6分）选②③均可
选②解方程，则这个方程为：x2+3x+1＝0，解得：
选③解方程，则这个方程为：x2+3x-1＝0，解得：
17.（6分）1.略；2.
18.（6分）解：（1）甲选择A景点的概率为，
故答案为：；
（2）根据题意画树状图如下：
∵共有9种等可能的情况，其中甲、乙两人中至少有一人选择C景点的情况有5种，
∴甲、乙两人中至少有一人选择C景点的概率是．
19（8分）解：（1）设y＝kx+b（k≠0），
将点（50，160），（80，100）代入得：，
解得：，
∴y与x的函数关系式为：y＝﹣2x+260；
（2）设每天获得的利润为w元，由题意得w＝（x﹣50）（﹣2x+260）＝﹣2x2+360x﹣13000＝﹣2（x﹣90）2+3200，
∵按照物价部门规定，销售单价不低于成本且不高于85元，
∴50≤x≤85，
∵a＝﹣2＜0，抛物线开口向下，
∴当50≤x≤85时，w随着x的增大而增大，
∴w有最大值，当x＝85时，w最大值＝3150，
∴销售单价为85元时，每天获得的利润最大，最大利润是3150元．
20（9分）解：（1）将A（，1）代入到y＝中，
得：1＝，
解得：k＝；
（2）过点A作OD的垂线，交x轴于G，
∵A（，1），
∴AG＝1，OG＝，
OA＝＝2，
∴半径为2；
∵AG＝OA，
∴∠AOG＝30°，
由菱形的性质可知，∠AOG＝∠COG＝60°，
∴∠AOC＝60°，
∴圆心角的度数为：60°；
（3）∵OD＝2OG＝2，
∴S菱形AOCD＝AG×OD＝2，
∴S扇形AOC＝×π×r2＝，
在菱形OBEF中，S△FHO＝S△BHO，
∵S△FHO＝＝，
∴S△FBO＝2×＝，
∴S阴影＝S△FBO+S菱形AOCD﹣S扇形AOC＝+2﹣π＝3﹣．
21.（8分）（1）证明：连接OD，
∵EQ \\ac(\S\UP7(⌒),AC)＝EQ \\ac(\S\UP7(⌒),CD)＝EQ \\ac(\S\UP7(⌒),DB)，∴∠BOD＝EQ \F(1,3)×180°＝60°，
∵EQ \\ac(\S\UP7(⌒),CD)＝EQ \\ac(\S\UP7(⌒),DB)，∴∠EAD＝∠DAB＝EQ \F(1,2)∠BOD＝30°，
∵OA＝OD，∴∠ADO＝∠DAB＝30°，
∵DE⊥AC，∴∠E＝90°，
∴∠EAD+∠EDA＝90°，∴∠EDA＝60°，
∴∠EDO＝∠EDA+∠ADO＝90°，∴OD⊥DE，
∴DE是⊙O的切线；
（2）解：连接BD，
∵AB为⊙O的直径，
∴∠ADB＝90°，
∵∠DAB＝30°，AB＝6，
∴BD＝EQ \F(1,2)AB＝3，
∴AD＝3EQ \R(,3)．
22.（10分）解：（1）b═，c═1．（2分）
（2）由y══，
可知当x═时，y有最大值，
故大棚最高处到地面的距离为米；（5分）
（3）令y═，则有═，解得x1═，x2═，
又∵0≤x≤6，∴大棚内可以搭建支架的土地的宽为6═（米），
又大棚的长为16米，∴需要搭建支架部分的土地面积为16═88（平方米），
故共需要88×4═352（根）竹竿，
答：共需要准备352根竹竿．（10分）
23（10分）解：（1）画出图形如下：
∵CA＝CB，∠C＝90°，
∴∠ABC＝45°，
∵BD⊥AB，
∴∠ABD＝90°，
∴∠PBD＝∠ABC+∠ABD＝45°+90°＝135°；
故答案为：135；（2分）
（2）PA＝PE，理由如下：
过P作PM∥AB交AC于M，如图：
∴∠MPC＝∠ABC＝45°，
∴△PCM是等腰直角三角形，
∴CP＝CM，∠PMC＝45°，
∴CA﹣CM＝CB﹣CP，即AM＝BP，∠AMP＝135°＝∠PBE，
∵∠APE＝90°，
∴∠EPB＝90°﹣∠APC＝∠PAC，
∴△APM≌△PEB（ASA），
∴PA＝PE；（6分）
（3）BE＝BA+BP，理由如下：
过P作PN⊥BC交BE于N，如图：
∵∠ABD＝90°，∠ABC＝45°，
∴∠PBN＝180°﹣∠ABC﹣∠ABD＝45°，
∴△BPN是等腰直角三角形，∠ABP＝135°，
∴BP＝NP，BN＝BP，∠PNB＝45°，
∴∠PNE＝135°＝∠ABP，
∵∠APE＝90°，
∴∠EPN＝90°﹣∠APN＝∠APB，
∴△EPN≌△APB（ASA），
∴EN＝BA，
∵BE＝EN+BN，
∴BE＝BA+BP．（10分）
24.（12分）解：任务1：
变化量分别为：29﹣30＝﹣1（cm）；28.1﹣29＝﹣0.9（cm）；27﹣28.1＝﹣1.1（cm）；25.8﹣27＝﹣1.2（cm），
∴每隔10min水面高度观察值的变化量为：﹣1，﹣0.9，﹣1.1，﹣1.2．（2分）
任务2：
设水面高度h与流水时间t的函数解析式为h＝kt+b，
∵t＝0 时，h＝30；t＝10时，h＝29；
∴，
解得：，
∴水面高度h与流水时间t的函数解析式为h＝﹣0.1t+30；（5分）
任务3：
（1）w＝（30﹣30）²+（29﹣29）2+（28﹣28.1）2+（27﹣27）2+（26﹣25.8）2
＝0.05．
（2）w＝（10k+30﹣30）2+（10k+30﹣29）2+（10k+30﹣28.1）2+（10k+30﹣27）2+（10k+30﹣25.8）2
＝3000（k+0.102）2﹣0.038，
∴当k＝﹣0.102时，w的最小值为0.038．（9分）
任务4：
在容器外壁每隔1.02cm标记一次刻度，这样水面每降低一个刻度，就代表时间经过了10分钟．（12分）
流水时间t/min
0
10
20
30
40
水面高度h/cm（观察值）
30
29
28.1
27
25.8