2021-2022学年安徽省合肥市庐江县八年级上学期期中数学试题及答案

这是一份2021-2022学年安徽省合肥市庐江县八年级上学期期中数学试题及答案，共25页。

生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号、
姓名是否一致．
2．选择题每小题选出答案后，用 2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改
动，用橡皮擦干净后，再选涂其他答案标号．非选择题答案用 0.5 毫米黑色墨水签字
笔在答题卡上相应位置书写作答，在试题卷上答题无效．
3．作图可先使用 2B 铅笔画出，确定后必须用 0.5 毫米黑色墨水签字笔描黑．
一、单选题（共40分）
1．如图图形是以科学家名字命名的，其中是轴对称图形的有（ ）
A．1个B．2个C．3个D．4个
2．打下列说法：①两个形状相同的图形称为全等图形；②边、角分别对应相等的两个多边形全等；③全等图形的形状、大小都相同；④面积相等的两个三角形全等．其中正确的是（ ）
A．①②③B．①②④C．①③D．②③
3．如图，将一副三角尺按如图所示的方式摆放，则∠α＝（ ）
A．45°B．60°C．75°D．90°
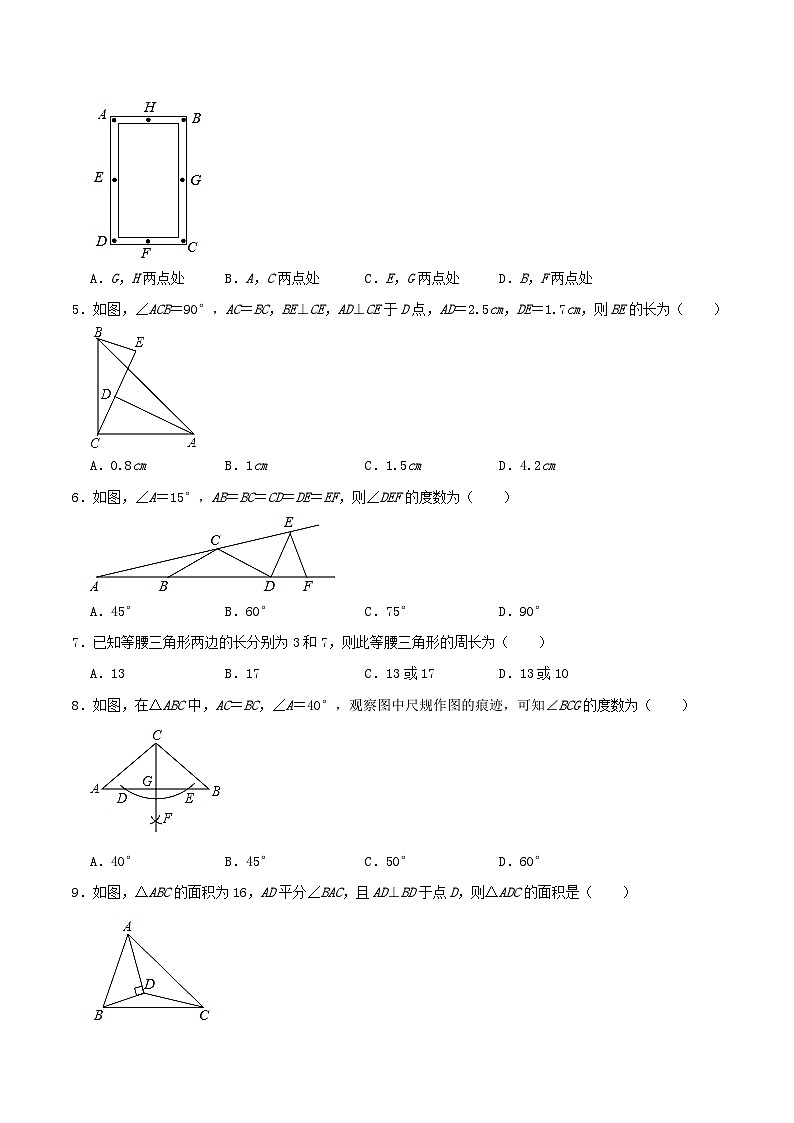
4．如图，工人师傅做了一个长方形窗框ABCD，E，F，G，H分别是四条边上的中点，为了稳固，需要在窗框上钉一根木条，这根木条不应钉在（ ）
A．G，H两点处B．A，C两点处C．E，G两点处D．B，F两点处
5．如图，∠ACB＝90°，AC＝BC，BE⊥CE，AD⊥CE于D点，AD＝2.5cm，DE＝1.7cm，则BE的长为（ ）
A．0.8cmB．1cmC．1.5cmD．4.2cm
6．如图，∠A＝15°，AB＝BC＝CD＝DE＝EF，则∠DEF的度数为（ ）
A．45°B．60°C．75°D．90°
7．已知等腰三角形两边的长分别为3和7，则此等腰三角形的周长为（ ）
A．13B．17C．13或17D．13或10
8．如图，在△ABC中，AC＝BC，∠A＝40°，观察图中尺规作图的痕迹，可知∠BCG的度数为（ ）
A．40°B．45°C．50°D．60°
9．如图，△ABC的面积为16，AD平分∠BAC，且AD⊥BD于点D，则△ADC的面积是（ ）
A．6B．8C．10D．12
10．如图，在△ABC中，点D、E在BC边上，点F在AC边上，将△ABD沿着AD翻折，使点B和点E重合，将△CEF沿着EF翻折，点C恰与点A重合．结论：①∠BAC＝90°，②DE＝EF，③∠B＝2∠C，④AB＝EC，正确的有（ ）
A．①②③④B．③④C．①②④D．①②③
二、填空题（共20分）
11．已知图中的两个三角形全等，则∠1＝ ．
12．如图，树AB垂直于地面，为测树高，小明在C处，测得∠ACB＝15°，他沿CB方向走了28米，到达D处，测得∠ADB＝30°，则树的高度是 ．
13．如图，在△ABC中，AB＝AC，AB＞BC，点D在边BC上，且CD＝2BD，点E，F在线段AD上，且满足∠BED＝∠CFD＝∠BAC，若S△ABC＝24，则S△ABE+S△CDF＝ ．
14．在△ABC中，∠ACB＝90°，∠A＜∠B，点D是AB边（不与端点重合）上一点，将△ACD沿CD翻折后得到△ECD，射线CE交射线AB于点F．
（1）若AD＝CD＝CF，则∠A＝ °；
（2）设∠A＝α，当∠ACD＝ 时（用含α的代数式表示，写出所有可能的结果），△DEF为等腰三角形．
三、解答题（本题共2小题，每小题8分，满分16分）
15．一个多边形的内角和是外角和的2倍，它是几边形？
16．如图所示：△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠BAC＝60°，∠C＝70°，求∠CAD，∠BOA的度数是多少？
四、解答题（本题共2小题，每小题8分，满分16分）
17．已知：如图，点A、B、C、D在一条直线上，EA∥FB，EA＝FB，AB＝CD．
（1）求证：∠E＝∠F；
（2）若∠A＝40°，∠D＝80°，求∠E的度数．
18．如图，AB与CD交于点F，BE与AC交于点G，AB＝AC，AF＝AG，∠D＝∠E．求证：AD＝AE．
五、解答题（体题共2小题，每小题解0分，满分20分）
19．如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣2，1），C（﹣1，3）．
（1）画出△ABC关于x轴的对称图形△A1B1C1．
（2）画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2．
（3）如果AC上有一点M（a，b）经过上述两次变换，那么对应A2C2上的点M2的坐标是 ．
（4）△ABC的面积为 ．
20．如图，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别是E，F，连接EF，EF与AD相交于点G．
（1）求证：AD是EF的垂直平分线；
（2）若△ABC的面积等于16，AB+AC＝8，求ED．
六、解答题（本题满分12分）
21．一天课间，顽皮的小明同学拿着老师的等腰直角三角板玩，不小心将三角板掉到了两墙之间，如图所示，AD⊥DE，BE⊥DE，∠ACB＝90°，点C在DE上．这一幕恰巧被数学老师看见了，于是有了下面这道题．
（1）试说明△ADC≌△CEB的理由；
（2）如果每块砖的厚度a＝10cm，请你帮小明求出两墙之间距离DE的长度．
七、解答题（本题满分12分）
22．如图，在△ABC中，点M、N分别为线段BC、AC上的动点，当M运动到线段BC的中点时有AM⊥BC．
（1）证明：AB＝AC；
（2）设线段AB的中点为D，当AB＝14cm，BC＝13cm时，若动点M从点B出发，以2cm/s的速度沿线段BC由点B向点C运动，动点N从点C出发匀速沿线段由点C向点A运动，动点M出发1秒后动点N才出发，直接写出当点N的运动速度为多少时，能够使△BMD与△CNM全等？
八、解答题（本题满分14分）
23．（1）（观察发现）如图1，△ABC和△CDE都是等边三角形，且点B、C、E在一条直线上，连接BD和AE，BD、AE相交于点P，则线段BD与AE的数量关系是 ，BD与AE相交构成的锐角的度数是 ．（只要求写出结论，不必说明理由）
（2）（深入探究1）如图2，△ABC和△CDE都是等边三角形，连接BD和AE，BD、AE相交于点P，猜想线段BD与AE的数量关系，以及BD与AE相交构成的锐角的度数．请说明理由．
（3）（深入探究2）如图3，△ABC和△CDE都是等腰直角三角形，且∠ACB＝∠DCE＝90°，连接AD、BE，Q为AD中点，连接QC并延长交BE于点K．求证：QK⊥BE．
参考答案
一、单选题（共40分）
1．如图图形是以科学家名字命名的，其中是轴对称图形的有（ ）
A．1个B．2个C．3个D．4个
【分析】如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，根据轴对称图形的概念求解．
解：第一、三两个图形均不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形，
第二、第四两个图形能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形，
故选：B．
2．打下列说法：①两个形状相同的图形称为全等图形；②边、角分别对应相等的两个多边形全等；③全等图形的形状、大小都相同；④面积相等的两个三角形全等．其中正确的是（ ）
A．①②③B．①②④C．①③D．②③
【分析】根据全等图形的定义即可判断①；根据多边形全等的判定定理即可判断②；根据全等多边形的性质即可判断③；化成图形，再根据全等三角形的判定定理即可判断④．
解：两个形状相同、大小也相同的图形称为全等图形，故①错误；
边、角分别对应相等的两个多边形全等，故②正确；
全等图形的形状、大小都相同，故③正确；
如图，△ABC和△DEF中，BC＝2，EF＝1，高AN＝1，高DM＝2，
△ABC和△DEF的面积都是＝1，
当时两三角形不全等，
即面积相等的两个三角形不一定全等，故④错误；
即正确的为②③，
故选：D．
3．如图，将一副三角尺按如图所示的方式摆放，则∠α＝（ ）
A．45°B．60°C．75°D．90°
【分析】根据三角形外角性质得出∠1，进而解答即可．
解：如图所示：
∵∠3＝30°，∠4＝45°，
∴∠2＝∠4﹣∠3＝45°﹣30°＝15°，
∴∠1＝∠2＝15°，
∴∠5＝90°﹣∠1＝90°﹣15°＝75°，
∴∠α＝∠5＝75°，
故选：C．
4．如图，工人师傅做了一个长方形窗框ABCD，E，F，G，H分别是四条边上的中点，为了稳固，需要在窗框上钉一根木条，这根木条不应钉在（ ）
A．G，H两点处B．A，C两点处C．E，G两点处D．B，F两点处
【分析】用木条固定长方形窗框，即是组成三角形，故可用三角形的稳定性解释．
解：工人师傅做了一个长方形窗框ABCD，工人师傅为了使它稳固，需要在窗框上钉一根木条，这根木条不应钉在E、G两点之间（没有构成三角形），这种做法根据的是三角形的稳定性．
故选：C．
5．如图，∠ACB＝90°，AC＝BC，BE⊥CE，AD⊥CE于D点，AD＝2.5cm，DE＝1.7cm，则BE的长为（ ）
A．0.8cmB．1cmC．1.5cmD．4.2cm
【分析】根据条件可以得出∠E＝∠ADC＝90°，进而得出△CEB≌△ADC，就可以得出BE＝DC，就可以求出BE的值．
解：∵BE⊥CE，AD⊥CE，
∴∠E＝∠ADC＝90°，
∴∠EBC+∠BCE＝90°．
∵∠BCE+∠ACD＝90°，
∴∠EBC＝∠DCA．
在△CEB和△ADC中，
，
∴△CEB≌△ADC（AAS），
∴BE＝DC．CE＝AD＝2.5．
∵DC＝CE﹣DE，DE＝1.7cm，
∴DC＝2.5﹣1.7＝0.8cm．
故选：A．
6．如图，∠A＝15°，AB＝BC＝CD＝DE＝EF，则∠DEF的度数为（ ）
A．45°B．60°C．75°D．90°
【分析】根据已知条件，利用等腰三角形的性质及三角形的内角和外角之间的关系进行计算．
解：∵AB＝BC＝CD＝DE＝EF，∠A＝15°，
∴∠BCA＝∠A＝15°，
∴∠CBD＝∠BDC＝∠BCA+∠A＝15°+15°＝30°，
∴∠ECD＝∠CED＝∠A+∠CDB＝45°
∴∠EDF＝∠EFD＝∠A+∠CED＝60°
∴∠DEF＝180°﹣（∠EDF+∠EFD）＝180°﹣120°＝60°．
故选：B．
7．已知等腰三角形两边的长分别为3和7，则此等腰三角形的周长为（ ）
A．13B．17C．13或17D．13或10
【分析】等腰三角形两边的长为3和7，具体哪条是底边，哪条是腰没有明确说明，因此要分两种情况讨论．
解：①当腰是3，底边是7时，不满足三角形的三边关系，因此舍去．
②当底边是3，腰长是7时，能构成三角形，则其周长＝3+7+7＝17．
故选：B．
8．如图，在△ABC中，AC＝BC，∠A＝40°，观察图中尺规作图的痕迹，可知∠BCG的度数为（ ）
A．40°B．45°C．50°D．60°
【分析】利用等腰三角形的性质和基本作图得到CG⊥AB，则CG平分∠ACB，利用∠A＝∠B和三角形内角和计算出∠ACB，从而得到∠BCG的度数．
解：由作法得CG⊥AB，
∵AC＝BC，
∴CG平分∠ACB，∠A＝∠B，
∵∠ACB＝180°﹣40°﹣40°＝100°，
∴∠BCG＝∠ACB＝50°．
故选：C．
9．如图，△ABC的面积为16，AD平分∠BAC，且AD⊥BD于点D，则△ADC的面积是（ ）
A．6B．8C．10D．12
【分析】延长BD交AC于点E，则可知△ABE为等腰三角形，则S△ABD＝S△ADE，S△BDC＝S△CDE，可得出S△ADC＝S△ABC．
解：如图，延长BD交AC于点E，
∵AD平分∠BAE，AD⊥BD，
∴∠BAD＝∠EAD，∠ADB＝∠ADE，
在△ABD和△AED中，
，
∴△ABD≌△AED（ASA），
∴BD＝DE，
∴S△ABD＝S△ADE，S△BDC＝S△CDE，
∴S△ABD+S△BDC＝S△ADE+S△CDE＝S△ADC，
∴S△ADC＝S△ABC＝×16＝8，
故选：B．
10．如图，在△ABC中，点D、E在BC边上，点F在AC边上，将△ABD沿着AD翻折，使点B和点E重合，将△CEF沿着EF翻折，点C恰与点A重合．结论：①∠BAC＝90°，②DE＝EF，③∠B＝2∠C，④AB＝EC，正确的有（ ）
A．①②③④B．③④C．①②④D．①②③
【分析】将△ABD沿着AD翻折，可得AB＝AE，∠B＝∠AEB，将△CEF沿着EF翻折，则△AEF≌△CEF，可得AE＝CE，∠C＝∠CAE，可求AB＝EC，∠B＝2∠C．
解：∵将△ABD沿着AD翻折，使点B和点E重合，
∴AB＝AE，∠B＝∠AEB，
∵将△CEF沿着EF翻折，点C恰与点A重合，
∴AE＝CE，∠C＝∠CAE，
∴AB＝EC，∴④正确；
∵∠AEB＝∠C+∠CAE＝2∠C，
∴∠B＝2∠C，故③正确；
故选：B．
二、填空题（共20分）
11．已知图中的两个三角形全等，则∠1＝ 47° ．
【分析】根据三角形内角和定理求出∠2，根据全等三角形的性质解答即可．
解：由三角形内角和定理得，∠2＝180°﹣60°﹣73°＝47°，
∵两个三角形全等，
∴∠1＝∠2＝47°，
故答案为：47°．
12．如图，树AB垂直于地面，为测树高，小明在C处，测得∠ACB＝15°，他沿CB方向走了28米，到达D处，测得∠ADB＝30°，则树的高度是 14米 ．
【分析】根据三角形外角的性质得到∠CAD＝∠ADB﹣∠ACB＝15°，根据等腰三角形的性质得到AD＝CD＝20，由直角三角形的性质即可得到结论．
解：∵∠ADB＝30°，∠ACB＝15°，
∴∠CAD＝∠ADB﹣∠ACB＝15°，
∴∠ACB＝∠CAD，
∴AD＝CD＝28（米），
又∵∠ABD＝90°，
∴AB＝AD＝14（米），
∴树的高度为14米．
故答案为：14米．
13．如图，在△ABC中，AB＝AC，AB＞BC，点D在边BC上，且CD＝2BD，点E，F在线段AD上，且满足∠BED＝∠CFD＝∠BAC，若S△ABC＝24，则S△ABE+S△CDF＝ 16 ．
【分析】根据△ABE≌△CAF得出△ACF与△ABE的面积相等，可得S△ABE+S△CDF＝S△ACD，即可得出答案．
解：∵∠BED＝∠CFD＝∠BAC，∠BED＝∠BAE+∠ABE，∠BAC＝∠BAE+∠CAF，∠CFD＝∠FCA+∠CAF，
∴∠ABE＝∠CAF，∠BAE＝∠FCA，
在△ABE和△CAF中，
，
∴△ABE≌△CAF（ASA），
∴S△ABE＝S△ACF，
∴S△ABE+S△CDF＝S△ACD，
∵S△ABC＝24，CD＝2BD，
∴S△ACD＝S△ABC＝16，
故答案为：16．
14．在△ABC中，∠ACB＝90°，∠A＜∠B，点D是AB边（不与端点重合）上一点，将△ACD沿CD翻折后得到△ECD，射线CE交射线AB于点F．
（1）若AD＝CD＝CF，则∠A＝ 36 °；
（2）设∠A＝α，当∠ACD＝ 90°﹣α或90°﹣α 时（用含α的代数式表示，写出所有可能的结果），△DEF为等腰三角形．
【分析】（1）由题意可得∠A＝∠ACD，∠CDF＝∠CFD，由折叠的性质可得∠ACD＝∠DCF，再由三角形的外角性质可得∠CDF＝∠A+∠ACD＝2∠A，利用三角形的内角和即可求∠A的度数；
（2）若△DEF为等腰三角形，则∠EDF＝∠E＝α，根据三角形外角的性质以及三角形内角和定理即可求得结果．
解：（1）如图，
∵AD＝CD＝CF，
∴∠A＝∠ACD，∠CDF＝∠CFD，
由折叠的性质可得∠ACD＝∠DCF＝∠A，
∵∠CDF是△ACD的一个外角，
∴∠CDF＝∠A+∠ACD＝2∠A，
∴∠CFD＝2∠A，
∵∠CDF+∠CFD+∠DCF＝180°，
∴2∠A+2∠A+∠A＝180°，
解得：∠A＝36°，
故答案为：36；
（2）解：由翻折的性质可知∠E＝∠A＝α，∠CDE＝∠ADC，
如图，
当EF＝DF时，则∠EDF＝∠E＝α，
∵∠EDF＝∠CDE﹣∠CDB，∠CDB＝∠A+∠ACD，
∴α＝∠ADC﹣（∠A+∠ACD）
＝180°﹣2（∠A+∠ACD）
＝180°﹣2（α+∠ACD），
∴∠ACD＝90°﹣，
∴当∠ACD＝90°﹣时，△DEF为等腰三角形，
当ED＝EF时，∠EDF＝∠EFD＝＝90°﹣α；
∴2∠ADC＝180°+∠EDF＝270°﹣，
∴∠ADC＝135°﹣α，
∴∠ACD＝180°﹣∠A﹣∠ADC＝180°﹣α﹣135°+α，＝45°﹣α；
∵∠DFE＝∠A+∠ACF，
∴∠DFE≠∠DEF，
如图，
当DE＝EF时，∠EDF＝∠EFD＝α；
∴∠ACF＝180°﹣∠A﹣∠EFD＝180°﹣α﹣，＝180°﹣α，
∴∠ACD＝∠ACF＝90°﹣α；
∴当∠ACD＝90°﹣α或90°﹣α时，△DEF为等腰三角形，
故答案为90°﹣α或90°﹣α．
三、解答题（本题共2小题，每小题8分，满分16分）
15．一个多边形的内角和是外角和的2倍，它是几边形？
【分析】多边形的外角和是360度，多边形的外角和是内角和的一半，则多边形的内角和是720度，根据多边形的内角和可以表示成（n﹣2）•180°，依此列方程可求解．
解：设多边形边数为n．
则360°×2＝（n﹣2）•180°，
解得n＝6．
故是六边形．
16．如图所示：△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠BAC＝60°，∠C＝70°，求∠CAD，∠BOA的度数是多少？
【分析】因为AD是高，所以∠ADC＝90°，又因为∠C＝70°，所以∠CAD度数可求；因为∠BAC＝60°，∠C＝70°，所以∠BAO＝30°，∠ABC＝50°，BF是∠ABC的角平分线，则∠ABO＝25°，故∠BOA的度数可求．
解：∵AD⊥BC，
∴∠ADC＝90°，
∵∠C＝70°，
∴∠CAD＝180°﹣90°﹣70°＝20°；
∵∠BAC＝60°，∠C＝70°，
∴∠BAO＝30°，∠ABC＝50°，
∵BF是∠ABC的角平分线，
∴∠ABO＝25°，
∴∠BOA＝180°﹣∠BAO﹣∠ABO＝180°﹣30°﹣25°＝125°．
故∠CAD，∠BOA的度数分别是20°，125°．
四、解答题（本题共2小题，每小题8分，满分16分）
17．已知：如图，点A、B、C、D在一条直线上，EA∥FB，EA＝FB，AB＝CD．
（1）求证：∠E＝∠F；
（2）若∠A＝40°，∠D＝80°，求∠E的度数．
【分析】（1）首先利用平行线的性质得出，∠A＝∠FBD，根据AB＝CD即可得出AC＝BD，进而得出△EAC≌△FBD解答即可；
（2）根据全等三角形的性质和三角形内角和解答即可．
【解答】证明：（1）∵EA∥FB，
∴∠A＝∠FBD，
∵AB＝CD，
∴AB+BC＝CD+BC，
即AC＝BD，
在△EAC与△FBD中，
，
∴△EAC≌△FBD（SAS），
∴∠E＝∠F；
（2）∵△EAC≌△FBD，
∴∠ECA＝∠D＝80°，
∵∠A＝40°，
∴∠E＝180°﹣40°﹣80°＝60°，
答：∠E的度数为60°．
18．如图，AB与CD交于点F，BE与AC交于点G，AB＝AC，AF＝AG，∠D＝∠E．求证：AD＝AE．
【分析】由“SAS”可证△AFC≌△AGB，可得∠AFC＝∠AGB，由“AAS”可证△ADF≌△AEG，可得AD＝AE．
【解答】证明：在△AFC和△AGB中，
，
∴△AFC≌△AGB（SAS），
∴∠AFC＝∠AGB，
∴∠AFD＝∠AGE，
在△ADF和△AEG中，
，
∴△ADF≌△AEG（AAS），
∴AD＝AE．
五、解答题（体题共2小题，每小题解0分，满分20分）
19．如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣2，1），C（﹣1，3）．
（1）画出△ABC关于x轴的对称图形△A1B1C1．
（2）画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2．
（3）如果AC上有一点M（a，b）经过上述两次变换，那么对应A2C2上的点M2的坐标是 （a+4，﹣b） ．
（4）△ABC的面积为 3 ．
【分析】（1）根据轴对称的性质即可作出△A1B1C1；
（2）根据平移的性质即可作出△A2B2C2；
（3）结合（1）（2）可得AC上有一点M（a，b）的横坐标加4，纵坐标互为相反数，即可得对应A2C2上的点M2的坐标．
（4）根据网格即可求出△ABC的面积．
解：（1）如图，△A1B1C1即为所求；
（2）如图，△A2B2C2即为所求；
（3）点M2的坐标是（a+4，﹣b）．
故答案为：（a+4，﹣b）．
（4）△ABC的面积为：2×4﹣1×4﹣1×2﹣2×2＝8﹣2﹣1﹣2＝3．
故答案为：3．
20．如图，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别是E，F，连接EF，EF与AD相交于点G．
（1）求证：AD是EF的垂直平分线；
（2）若△ABC的面积等于16，AB+AC＝8，求ED．
【分析】（1）先利用角平分线的性质得到DE＝DF，则可根据“HL”判断Rt△AED≌Rt△AFD，所以AE＝AF，然后根据线段垂直平分线的性质定理的逆定理得到结论；
（2）根据三角形面积公式，利用S△ABD+S△ACD＝S△ABC得到•AB•DE+•AC•DF＝16，然后利用DE＝DF和AB+AC＝8可求出DE的长．
【解答】（1）证明：∵AD是△ABC的角平分线，DE⊥AB，DF⊥AC，
∴DE＝DF，∠AED＝∠AFD＝90°，
在Rt△AED和Rt△AFD中，
，
∴Rt△AED≌Rt△AFD（HL），
∴AE＝AF，
而DE＝DF，
∴AD是EF的垂直平分线；
（2）解：∵S△ABD+S△ACD＝S△ABC，
∴•AB•DE+•AC•DF＝16，
∵DE＝DF，AB+AC＝8，
∴×DE×8＝16，
∴DE＝4．
六、解答题（本题满分12分）
21．一天课间，顽皮的小明同学拿着老师的等腰直角三角板玩，不小心将三角板掉到了两墙之间，如图所示，AD⊥DE，BE⊥DE，∠ACB＝90°，点C在DE上．这一幕恰巧被数学老师看见了，于是有了下面这道题．
（1）试说明△ADC≌△CEB的理由；
（2）如果每块砖的厚度a＝10cm，请你帮小明求出两墙之间距离DE的长度．
【分析】（1）由AAS证明△ADC≌△CEB即可；
（2）由全等三角形的性质得出AD＝4a＝40cm＝CE，BE＝3a＝30cm＝DC，得出DE＝70cm．
【解答】（1）证明：由题意得：AC＝BC，∠ACB＝90°，AD⊥DE，BE⊥DE，
∴∠ADC＝∠CEB＝90°
∴∠ACD+∠BCE＝90°，∠ACD+∠DAC＝90°，
∴∠BCE＝∠DAC，
在△ADC和△CEB中，
，
∴△ADC≌△CEB（AAS）；
（2）解：由题意得：
∵△ADC≌△CEB，a＝10cm，
∴AD＝4a＝40cm＝CE，BE＝3a＝30cm＝DC，
∴DE＝70cm．
七、解答题（本题满分12分）
22．如图，在△ABC中，点M、N分别为线段BC、AC上的动点，当M运动到线段BC的中点时有AM⊥BC．
（1）证明：AB＝AC；
（2）设线段AB的中点为D，当AB＝14cm，BC＝13cm时，若动点M从点B出发，以2cm/s的速度沿线段BC由点B向点C运动，动点N从点C出发匀速沿线段由点C向点A运动，动点M出发1秒后动点N才出发，直接写出当点N的运动速度为多少时，能够使△BMD与△CNM全等？
【分析】（1）利用线段的垂直平分线的性质证明即可．
（2）设点N的运动速度为xcm/s，经过ts后△BMD与△CNM全等，由题意BM＝2（t+1）cm，CM＝[13﹣2（t+1）]cm，CN＝xtcm，分两种情形：①当BD＝CM，BM＝CN时，两三角形全等．②当BM＝CM，BD＝CN时，两三角形全等．分别构建方程求解即可．
【解答】（1）证明：∵当M运动到线段BC的中点时有AM⊥BC，
∴AM垂直平分线段BC，
∴AB＝AC．
（2）解：设点N的运动速度为xcm/s，经过ts后△BMD与△CNM全等，
由题意BM＝2（t+1）cm，CM＝[13﹣2（t+1）]cm，CN＝xtcm，
∵AB＝AC，
∴∠B＝∠C，
根据全等三角形的判定定理可知，有两种情形：
①当BD＝CM，BM＝CN时，两三角形全等．则有13﹣2（t+1）＝7且2（t+1）＝xt，
解得x＝3．
②当BM＝CM，BD＝CN时，两三角形全等．则有2（t+1）＝13﹣2（t+1）且7＝xt，
解得x＝，
综上所述，满足条件的点N的速度为3cm/s或cm/s时，两三角形全等．
八、解答题（本题满分14分）
23．（1）（观察发现）如图1，△ABC和△CDE都是等边三角形，且点B、C、E在一条直线上，连接BD和AE，BD、AE相交于点P，则线段BD与AE的数量关系是 相等 ，BD与AE相交构成的锐角的度数是 60° ．（只要求写出结论，不必说明理由）
（2）（深入探究1）如图2，△ABC和△CDE都是等边三角形，连接BD和AE，BD、AE相交于点P，猜想线段BD与AE的数量关系，以及BD与AE相交构成的锐角的度数．请说明理由．
（3）（深入探究2）如图3，△ABC和△CDE都是等腰直角三角形，且∠ACB＝∠DCE＝90°，连接AD、BE，Q为AD中点，连接QC并延长交BE于点K．求证：QK⊥BE．
【分析】（1）根据等边三角形的性质可得AB＝AC，CD＝CE，∠ACB＝∠DCE＝60°，然后求出∠ACE＝∠BCD，再利用“边角边”证明△ACE和△BCD全等，根据全等三角形对应边相等可得BD＝AE，根据全等三角形对应角相等可得∠AEC＝∠BDC，然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠DPE＝∠DCE；
（2）证明△ACE≌△BCD（SAS），由全等三角形的性质得出BD＝AE，∠AEC＝∠BDC，则可得出结论；
（3）延长CQ到R，使得CQ＝QR，连接AR、DR．只要证明△ACR≌△BCE，可得∠ACR＝∠CBE，由∠ACR+∠BCK＝90°，推出∠CBE+∠BCK＝90°，可得∠CKB＝90°，即QK⊥BE．
解：（1）∵△ABC和△CDE都是等边三角形，
∴AB＝AC，CD＝CE，∠ACB＝∠DCE＝60°，
∴∠ACB+∠ACD＝∠DCE+∠ACD，
即∠ACE＝∠BCD，
在△ACE和△BCD中，
，
∴△ACE≌△BCD（SAS），
∴BD＝AE，∠AEC＝∠BDC，
由三角形的外角性质，∠DPE＝∠AEC+∠BDC，
∠DCE＝∠BDC+∠DBC，
∴∠DPE＝∠DCE＝60°；
故答案为：相等，60°；
（2）BD＝AE，BD与AE相交构成的锐角的度数为60°．
证明：∵△ABC和△CDE都是等边三角形，
∴AB＝AC，CD＝CE，∠ACB＝∠DCE＝60°，
∴∠ACB+∠ACD＝∠DCE+∠ACD，
即∠ACE＝∠BCD，
在△ACE和△BCD中，
，
∴△ACE≌△BCD（SAS），
∴BD＝AE，∠AEC＝∠BDC，
又∵∠DNA＝∠ENC，
∴∠DPE＝∠DCE＝60°．
（3）延长CQ到R，使得CQ＝QR，连接AR、DR．
∵△ABC和△CDE都是等腰直角三角形，
∴∠ACB＝∠DCE＝90°，AC＝BC，CE＝CD，
∴∠BCE+∠ACD＝180°，
∵AQ＝DQ，CQ＝QR，
∴四边形ACDR是平行四边形，
∴AR＝CD＝CE，AR∥CD，
∴∠CAR+∠ACD＝180°，
∴∠BCE＝∠CAR，
∵CA＝CB，AR＝CE，
∴△ACR≌△BCE（SAS），
∴∠ACR＝∠CBE，
∵∠ACR+∠BCK＝90°，
∴∠CBE+∠BCK＝90°，
∴∠CKB＝90°，即QK⊥BE．