江苏省南京市联合体2023～2024学年度第一学期期末九年级数学练习卷

这是一份江苏省南京市联合体2023～2024学年度第一学期期末九年级数学练习卷，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共6小题，每小题2分，共12分．）
1．方程 x2＋2x＝0的解是（ ）
2．二次函数y＝(x－1)2－3的图像顶点坐标是（ ）
3.在相同条件下的多次重复试验中，一个随机事件发生的频率为f，该事件的概率为P.下列
说法正确的是（ ）
A．试验次数越多，f越大
B．f与P都可能发生变化
C．试验次数越多，f越接近于P
D．试验次数很大时，f在P附近摆动，并趋于稳定
4．如图，OA是⊙O的半径，弦BC⊥OA，D是优弧 eq \(\s\up 5(⌒),BC)上一点，如果∠AOB＝58º，那么
∠ADC的度数为（ ）
5．如图，在△ABC中，AD是边BC上的中线，点E在边AC上，且AE∶EC＝1∶2，BE交AD于点P，则AP∶PD等于（ ）
6．已知二次函数y＝ax2＋bx＋c（0＜a＜b）的图像与x轴最多有一个公共点，现有四个结论：①该抛物线的对称轴在y轴的左侧；②关于x的方程ax2＋bx＋c＋2＝0无实数根；
③a－b＋c≥0．其中所有正确结论的序号是（ ）
二、填空题（本大题共10小题，每小题2分，共20分．）
7．在比例尺为1∶500 000的地图上，量得A、B两地的距离为3 cm，则A、B两地的实际距离为 km．
8．设x1，x2是方程x2＋x－4＝0的两根，则x12＋2x1＋x2＝ ．
9．如图，一个可以自由转动的转盘，任意转动转盘一次，当转盘停止时，指针落在红色区域的概率为 ．
10．若圆锥的底面半径为3 cm，高为4 cm，则圆锥侧面展开图的面积是 cm2．
11．在△ABC中，∠C＝90°，CD⊥AB，AD＝1，BD＝4，则CD的长为 ．
12．已知点P是线段AB的黄金分割点，PA＞PB，AB＝2 cm，则PA＝ cm．
13．如图，四边形ABCD内接于⊙O，AB是⊙O的直径，过点C作⊙O的切线交AB的延长线于点P，若∠P＝40°，则∠ADC＝ °．
（第13题）
A
O
P
D
C
B
（第14题）
2
3
3
O
x
y
红色
蓝色
120°
14．二次函数y＝ax2＋bx＋c（a≠0）的图像如图所示，当y＜3时，x的取值范围是 ．
（第9题）
15．方程x2＋│x－1│－1＝0的解是 ．
16．矩形ABCD的边长AD＝6，AB＝4，E，F分别为AB、BC的中点，AF分别与DE，DB相交于点M，N．则MN的长为 ．
三、解答题（本大题共11小题，共88分．解答时应写出文字说明、证明过程或演算步骤）
17．（8分）解方程
（1）x2－4x－5＝0； （2） (2x－1)2＝2x－1．
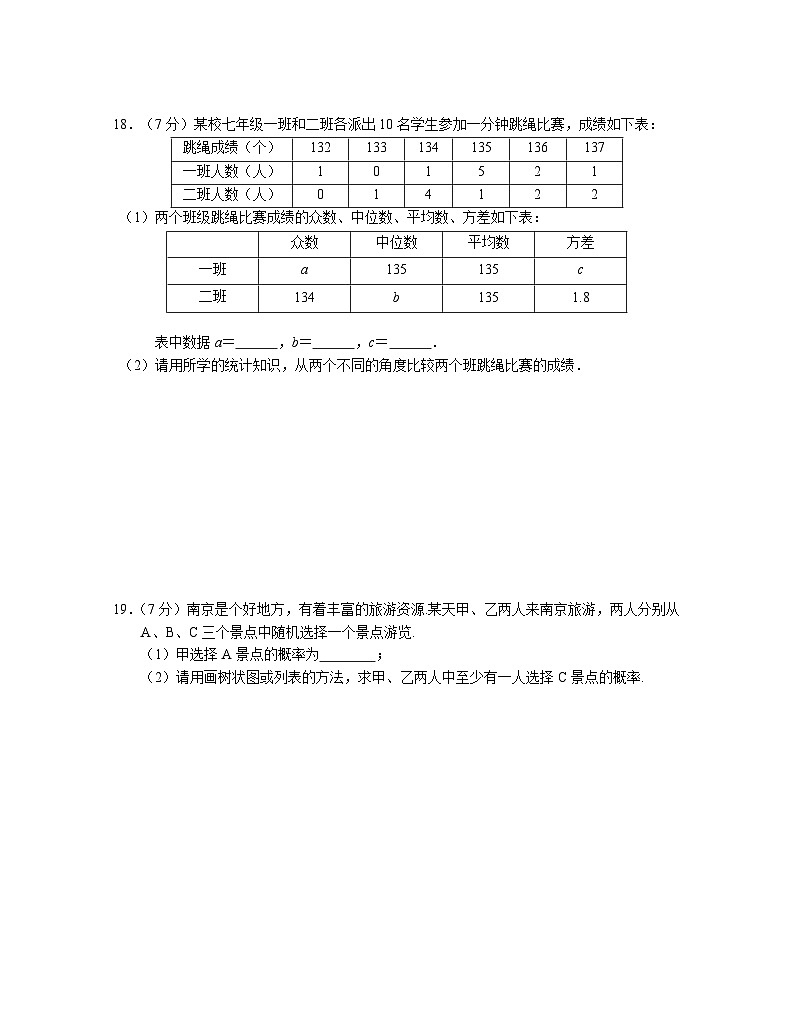
18．（7分）某校七年级一班和二班各派出10名学生参加一分钟跳绳比赛，成绩如下表：
（1）两个班级跳绳比赛成绩的众数、中位数、平均数、方差如下表：
表中数据a＝ ，b＝ ，c＝ ．
（2）请用所学的统计知识，从两个不同的角度比较两个班跳绳比赛的成绩．
19．（7分）南京是个好地方，有着丰富的旅游资源.某天甲、乙两人来南京旅游，两人分别从A、B、C三个景点中随机选择一个景点游览.
（1）甲选择A景点的概率为 ；
（2）请用画树状图或列表的方法，求甲、乙两人中至少有一人选择C景点的概率.
20．（7分）已知二次函数y＝ax2＋bx＋c（a≠0）中，函数y与自变量x的部分对应值如下表：
（1）求该二次函数的表达式；
（2）将该二次函数的图像向右平移1个单位，再向上平移2个单位，得到的图像所对应的函数表达式 ．
E
A
D
C
B
（第21题）
21. （7分）如图，分别以△ABC的边AC和BC为腰向外作等腰直角△DAC和等腰直角△EBC，连接DE.
（1）求证：△DAC∽△EBC；
（2）直接写出 eq \f(AB,DE) 的值．
A
C
E
D
B
O
(第22题)
22．（8分）如图，AB是⊙O的直径，AC是⊙O的弦，∠BAC的平分线交⊙O于点D，过点D作DE⊥AC交AC的延长线于点E，连接BD．
（1）求证：DE是⊙O的切线；
（2）若AE＝4，AB＝5，则AD＝ ．
23．（8分）某零售商购进一批单价为16元的玩具，销售一段时间后，为了获得更大利润，商店决定提高销售价格，经试验发现，当销售单价为20元时，每月能卖360件；若按每月25元的价格销售时，每月能卖210件.假定每月销售件数y件是价格x（单位：元）的一次函数.
（1）求y与x之间的关系式；
（2）在商品不积压且不考虑其他因素条件下，销售价格是多少时，才能使每月获得最大利润?最大利润是多少?
24．（8分）要修一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高，高度为3m，水柱落地处离池中心3m，求水管的长．
(第24题)
25．（8分）尺规作图，保留痕迹，写出必要的文字说明．
（1）如图①，已知线段MN，求作点P，使∠MPN＝135°；
M
N

(图①)
（2）如图②，已知线段m，求作Rt△ABC，使得A，B在线段m上，∠ACB＝90°，AC≠BC，且AB＋BC＋CA＝m．
m
(图②)
26．（9分）如图，AC，BD是⊙O的切线，C，D为切点，连接AB．
（1）若AB与⊙O相切于点E，求证AC＋BD＝AB；
（2）若AC＋BD＝AB，求证AB与⊙O相切．
(第（1）题图 )
A
B
C
O
D
E
A
B
C
O
D
(第（2）题图 )

27．（11分）已知二次函数y＝(x－m－4)(x＋m)，其中m为常数．
（1）求证：不论m为何值，该二次函数的图像与x轴有公共点．
（2）设该二次函数的图像与x轴的两个交点为A，B，该二次函数的图像顶点为P，若
△PAB为等腰直角三角形，直接写出m的值．
（3）若m＝1，点C，D都在该二次函数的图像上，且CD∥x轴，以CD为直径的圆恰好与x轴相切，求CD的长．
A． x1＝1，x2＝2
B．x1＝0，x2＝－2
C．x1＝0，x2＝2
D．x1＝1，x2＝－2
A．（－1，3）
B．（－1，－3）
C．（1，3）
D．（1，－3）
（第4题）
D
B
C
O
A
A
B
C
D
E
（第5题）
P
A． 32º
B．29º
C．58º
D．116º
A．1∶1
B．1∶2
C．2∶3
D．4∶3
A． = 1 \* GB3 ① = 2 \* GB3 ②
B． = 2 \* GB3 ② = 3 \* GB3 ③
C． = 1 \* GB3 ① = 3 \* GB3 ③
D． = 1 \* GB3 ① = 2 \* GB3 ② = 3 \* GB3 ③
跳绳成绩（个）
132
133
134
135
136
137
一班人数（人）
1
0
1
5
2
1
二班人数（人）
0
1
4
1
2
2
众数
中位数
平均数
方差
一班
a
135
135
c
二班
134
b
135
1.8
x
…
－2
－1
0
1
2
…
y
…
5
0
－3
－4
－3
…