数学人教版26.1.2 反比例函数的图象和性质图文ppt课件

这是一份数学人教版26.1.2 反比例函数的图象和性质图文ppt课件，共24页。PPT课件主要包含了挑战“记忆”，活动三，k＞0，k＜0，活动四，知识归纳，课堂检测，k－1，火炼真金，拓展训练等内容，欢迎下载使用。

问题：你还记得正比例函数y=kx (k≠0)的图象是什么样子吗?怎样得出来的?它的性质又是什么呢？
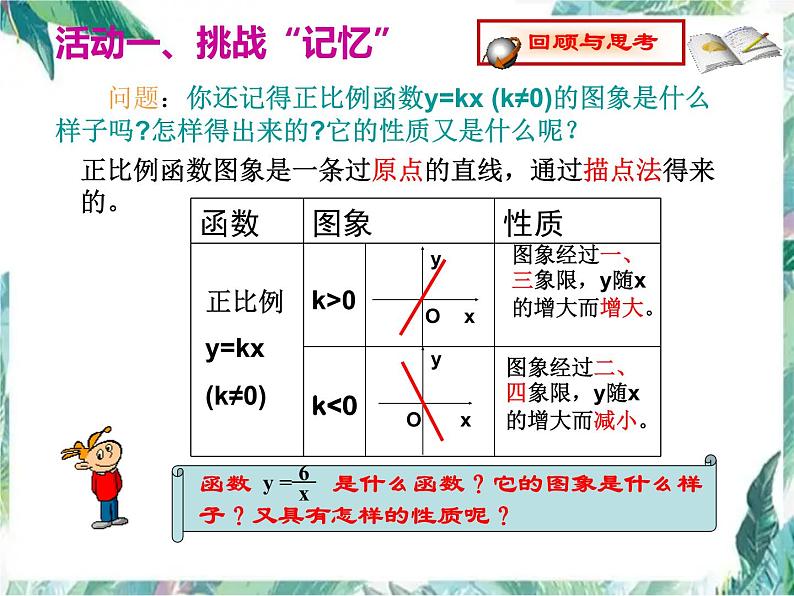
正比例函数图象是一条过原点的直线，通过描点法得来的。
正比例y=kx(k≠0)
图象经过一、三象限，y随x的增大而增大。
图象经过二、四象限，y随x的增大而减小。
1、经历探索反比例函数的性质的过程，体会函数的三种表达方式之间的联系和转化，发展数形结合的意识与能力。
2、能画出反比例函数的图像，进一步掌握画函数图像的步骤。
3、理解和掌握反比例函数的性质。
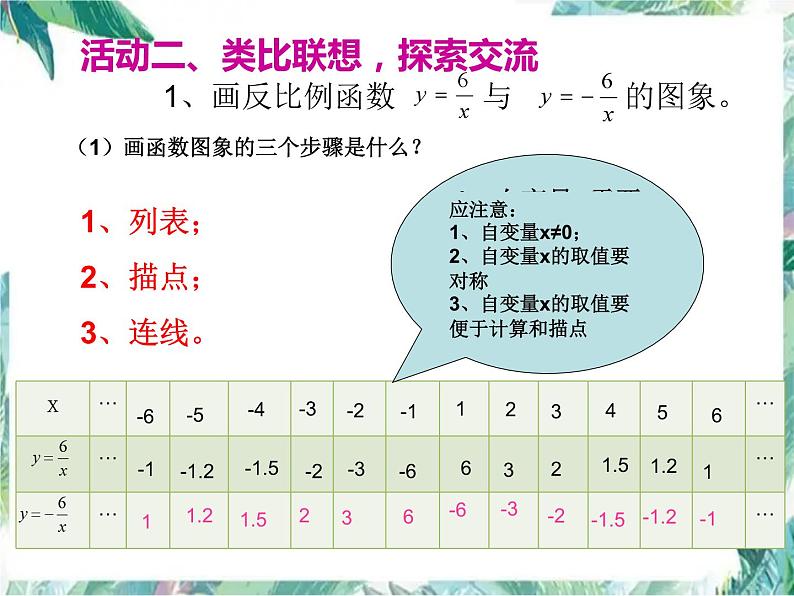
1、画反比例函数 与 的图象。
（1）画函数图象的三个步骤是什么？
1、自变量x需要取多少值?为什么?2、取值时要注意什么?
1、在不知道图象的走向的情况下，取点越多越能反映图象的实际情况，但一般取8—12个值为宜
应注意：1、自变量x≠0；2、自变量x的取值要对称3、自变量x的取值要便于计算和描点
1、列表；2、描点；3、连线。
活动二、类比联想，探索交流
你认为作反比例函数图象时应注意哪些问题？（列表时，描点时和连线时）
列表时，自变量的值可以选取一些互为相反数的值,这样既可简化计算,又便于对称性描点;列表描点时,要尽量多取一些数值,多描一些点,这样既可以方便连线,又较准确地表达函数的变化趋势;连线时，一定要养成按自变量从小到大的顺序，依次用平滑的曲线连接,从中体会函数的增减性；……
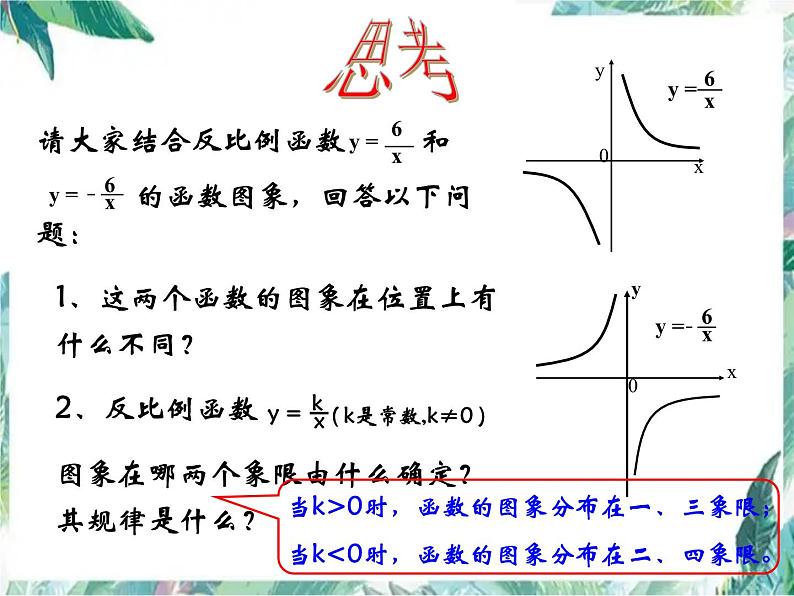
1、这两个函数的图象在位置上有 什么不同？2、反比例函数 图象在哪两个象限由什么确定？其规律是什么？
请大家结合反比例函数 和 的函数图象，回答以下问题：
当k>0时，函数的图象分布在一、三象限；当k<0时，函数的图象分布在二、四象限。
仔细看一看 认真想一想
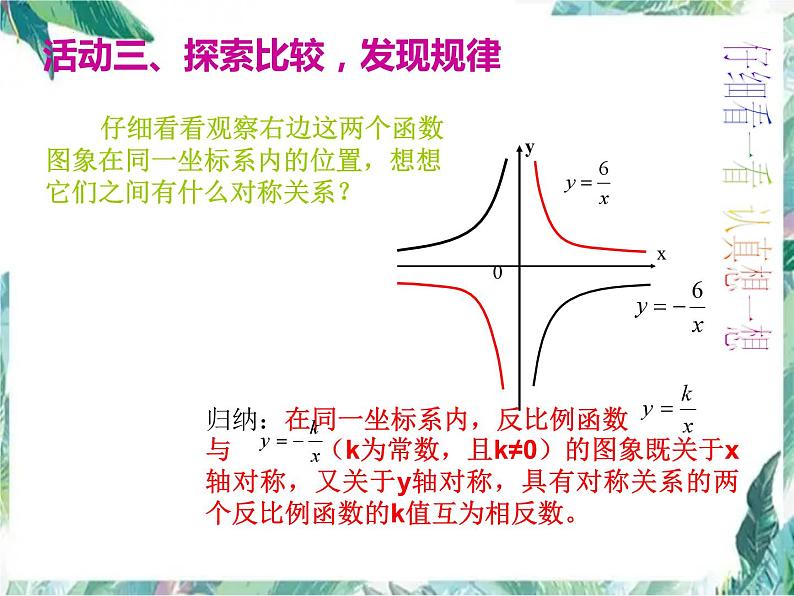
仔细看看观察右边这两个函数图象在同一坐标系内的位置，想想它们之间有什么对称关系？
活动三、探索比较，发现规律
看一看 想一想 议一议
1、每个函数的图象是什么形状，有几支？
函数有两条曲线，称为双曲线，有两个分支。
2、每个函数的图象所在的象限与k有什么关系？
当k＞0时，图象在第一、三象限，当k＜0时，图象在第二、四象限。
3、在每一个象限内，y的值随x的值怎样变化？与k有何关系？
当k＞0时，在每一个象限内，y随x的增大而减小；当k＜0时，在每一个象限内，y随x 的增大而增大。
4、它们的图象会与坐标轴相交吗？为什么？
反比例函数的图象可无限接近两坐标轴，但永远不会与坐标轴相交。
反比例函数是不是由k决定其性质呢?
( x≠0, y≠0 )
y=kx ( k≠0 )
每个象限内，y随x的增大而减小
每个象限内，y随x的增大而增大。
1、双曲线越来越接近两坐标轴，但永远不会与坐标轴相交。
三、运用新知 拓展训练
（ ）
1.下列函数中，其图象位于第一、三象限的有____________;在其所在的象限内，y随x的增大而增大的有___________.
2.若关于x,y的函数 图象位于第一、三象限， 则k的取值范围是_______________
3.甲乙两地相距100km，一辆汽车从甲地开往乙地，把汽车到达乙地所用的时间y(h)表示为汽车的平均速度x(km/h)的函数，则这个函数的图象大致是（ ）
在实际问题中图象就可能只有一支.
4.(1)已知点A(-2,y1),B(-1,y2),C(3,y3)都在反比例函数 的图象上，比较y1、 y2 、y3的大小关系。
解：∵k=4>0 ∴图象在第一、三象限内，每一象限内y随x的增大而减小 ∵x10, ∴点A(-2,y1)，点B(-1,y2)在第三象限点C(3,y3)在第一象限。 ∴y3>0, y2 你能解答第(2)小题吗了?
解：当K>0时, y2 < y1 < 0< y3.
当K＜0时, y3 < 0 < y1 < y2.
5、 已知k<0,则函数 y1=kx,y2= 在同一坐标系中的图象大致是 ( )
6、在反比例函数 图象的每一支曲线上， y都x随的增大而减小，则k的取值范围是什么？7、如果点（a,-2a）在双曲线上，那么在第几象限内，y随x的增大而__________
8、若点 在函数 （x＜0）的图象上，且 ，则它的图象大致是（ ）
1.通过本节课的学习，你有什么收获？还有什么困惑吗？2.你对自己本节课的表现满意吗？为什么？
肯请各位老师批评指导！