海南省省直辖县级行政单位乐东黎族自治县2023-2024学年七年级（上）学期期末数学试卷（含解析）

这是一份海南省省直辖县级行政单位乐东黎族自治县2023-2024学年七年级（上）学期期末数学试卷（含解析），共13页。试卷主要包含了5 毫米黑色墨水签字，56，33等内容，欢迎下载使用。

生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号、
姓名是否一致．
2．选择题每小题选出答案后，用 2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改
动，用橡皮擦干净后，再选涂其他答案标号．非选择题答案用 0.5 毫米黑色墨水签字
笔在答题卡上相应位置书写作答，在试题卷上答题无效．
3．作图可先使用 2B 铅笔画出，确定后必须用 0.5 毫米黑色墨水签字笔描黑．
一、单选题
1．在0，2，，这四个数中，最小的数是（ ）
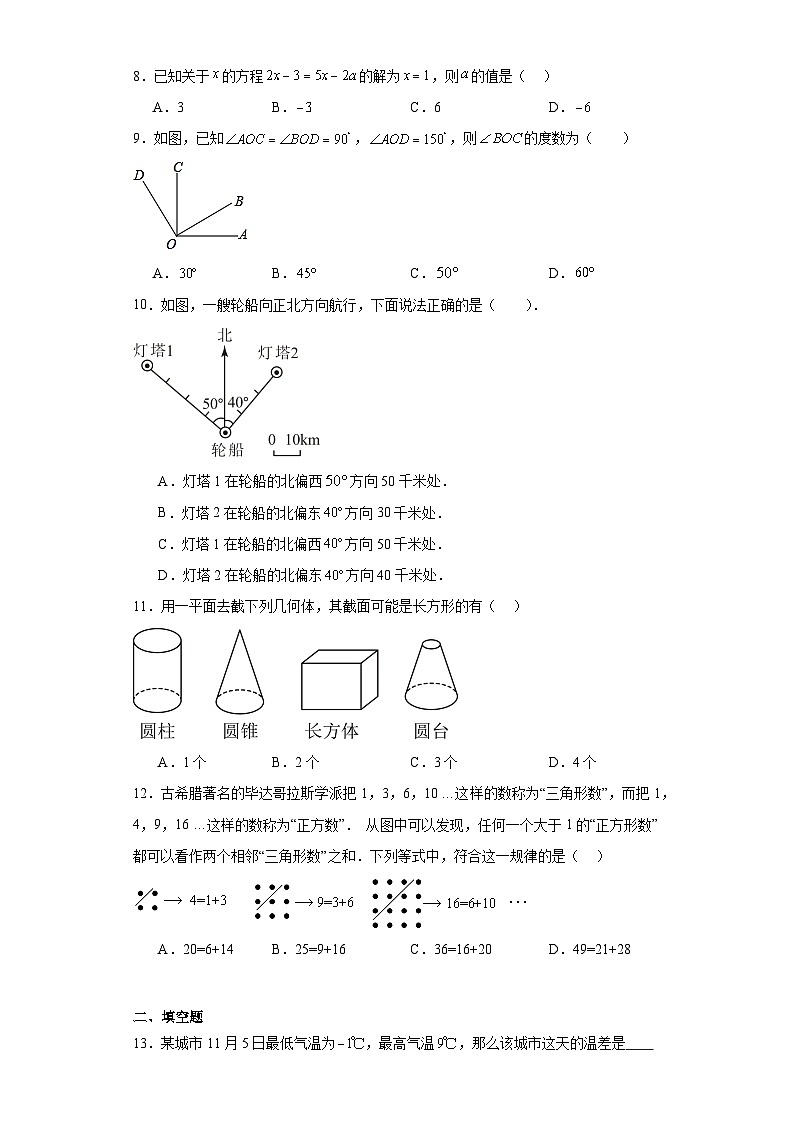
A．0B．2C．D．
2．下列各数中，与互为相反数的是（ ）
A．2B．﹣2C．D．-
3．2023年10月26日神舟十七号载人飞船发射取得圆满成功，我国载人航天工程发射任务实现30战30捷，航天员在中国空间站俯瞰地球的高度约为400000米，将400000用科学记数法表示应为（ ）
A．B．C．D．
4．下列是根据等式的性质进行变形，正确的是（ ）
A．若，则B．若，则
C．若，则D．若，则
5．如果一个有理数的绝对值是8，那么这个数一定是（ ）
A．-8B．-8或8C．8D．以上都不对
6．若与是同类项，则的值是（ ）
A．B．2C．3D．
7．下列说法正确的是（ ）
A．的次数是3B．多项式的次数是2
C．的系数是D．的次数是2
8．已知关于的方程的解为，则的值是（ ）
A．3B．C．6D．
9．如图，已知，，则的度数为（ ）
A．B．C．D．
10．如图，一艘轮船向正北方向航行，下面说法正确的是（ ）．

A．灯塔1在轮船的北偏西方向50千米处．
B．灯塔2在轮船的北偏东方向30千米处．
C．灯塔1在轮船的北偏西方向50千米处．
D．灯塔2在轮船的北偏东方向40千米处．
11．用一平面去截下列几何体，其截面可能是长方形的有（ ）

A．1个B．2个C．3个D．4个
12．古希腊著名的毕达哥拉斯学派把1，3，6，10 …这样的数称为“三角形数”，而把1，4，9，16 …这样的数称为“正方数”． 从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是（ ）
A．20=6+14B．25=9+16C．36=16+20D．49=21+28
二、填空题
13．某城市11月5日最低气温为，最高气温，那么该城市这天的温差是 ．
14．已知代数式的值是3，则代数式的值为 ．
15．如果，那么 ．
16．如图，直线，交于点．射线平分，若，则等于 ．
三、解答题
17．计算：
（1）
（2）
18．解方程
(1)
(2)
19．先化简，再求值：，其中，．
20．如图所示，点C是线段AB上的一点，点D是线段AB的中点，点E是线段BC的中点．
（1）当AC=8，BC=6时，求线段DE的长度；
（2）当AC=m，BC=n（m＞n）时，求线段DE的长度；
（3）从（1）（2）的结果中，你发现了什么规律？请直接写出来．
21．2018年8月1日，郑州市物价局召开居民使用天然气销售价格新闻通气会，宣布郑州市天然气价格调整方案如下：
（1）若张老师家9月份使用天然气36立方米，则需缴纳天然气费为______元；
（2）若张老师家10月份使用天然气立方米，则需缴纳的天然气费为_______元；
（3）依此方案计算，若张老师家11月份实际缴纳天然气费201.26元，求张老师家11月份使用天然气多少立方米？
22．数学活动课上，老师先在黑板上画出两条直线，再将三角板（，与直线a相交于点A）放在黑板上，转动三角板得到下面三个不同位置的图形．
(1)如图1，若点B在直线b上，，则 ；
(2)如图2，若点B在直线a的下方，在直线b的上方，与有怎样的关系？写出结论，并给出证明；
(3)如图3，若点B在直线b的下方，请写出与之间的关系并说明理由．
一户居民一个月天然气用量的范围
天然气价格（单位：元/立方米）
不超过50立方米
2.56
超过50立方米的部分
3.33
参考答案：
1．D
【分析】根据有理数比较大小的方法，即可得出答案．
【详解】解：根据有理数的比较大小，先比较符号，正数大于负数，正数相比较，绝对值大的数大，负数相比较，绝对值大的数反而小，正数大于零大于负数可得：，
即最小的数是．
故选D．
【点睛】本题主要考查有理数的比较大小，先比较符号，正数大于负数，正数相比较，绝对值大的数大，负数相比较，绝对值大的数反而小，正数大于零大于负数．
2．C
【分析】根据只有符号不同的两个数互为相反数即可得出答案．
【详解】解：因为与只有符号不同，
所以与互为相反数的是．
故选C．
【点睛】本题考查了相反数的概念，题目较简单，熟记相反数的概念是解决此题的关键．
3．A
【分析】此题主要考查了用科学记数法表示较大的数，一般形式为，其中，确定a与n的值是解题的关键．确定本题中的，，从而可得答案．
【详解】解：，
故选A
4．D
【分析】本题考查等式的性质，根据等式的性质，逐一进行判断即可．熟练掌握等式的性质是解题的关键．
【详解】解：A、若，则，选项错误；
B、若，则，选项错误；
C、若，，则，选项错误；
D、若，则，选项正确；
故选D．
5．B
【分析】根据绝对值的性质求解即可．
【详解】解：如果一个有理数的绝对值是8，那么这个数一定是−8或8．
故选B．
【点睛】本题考查了绝对值的知识，注意绝对值的性质：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．
6．D
【分析】本题考查同类项的概念应用．所含字母相同，并且相同字母的指数也相同的项叫做同类项．根据同类项的定义得出，，代入进行计算即可得出答案，熟练掌握同类项的定义是解此题的关键．
【详解】解：∵与是同类项，
∴，，
∴．
故选：D．
7．C
【分析】根据多项式，单项式的系数和次数的定义，逐项判断即可求解．
【详解】解：A、的次数是，故本选项错误，不符合题意；
B、多项式的次数是4，故本选项错误，不符合题意；
C、的系数是，故本选项正确，符合题意；
D、的次数是3，故本选项错误，不符合题意；
故选：C
【点睛】本题主要考查了多项式，单项式的系数和次数的定义，熟练掌握单项式中的数字因式是单项式的系数，所有字母的次数之和是单项式的次数；多项式的次数：多项式中最高次项的次数，叫做多项式的次数是解题的关键．
8．A
【分析】本题考查了一元一次方程的解，把代入中，即可求出a的值．
【详解】解：根据题意，关于的方程的解为，
把代入中，得：
，
解得：，
故选：A．
9．A
【分析】由，，根据角与角之间的关系可求出的度数，．
【详解】解：∵，，
∴
．
故选：A．
【点睛】此题考查的知识点是角的计算，注意此题的解题技巧：两个直角相加和相比，多加了一次．
10．B
【分析】本题重点考查以方向和距离确定物体位置的方法，解答时关键在于读懂图中方向和比例尺．
【详解】解：A、灯塔1在轮船的北偏西方向40千米处，故原说法错误，不符合题意；
B、灯塔2在轮船的北偏东方向30千米处，故原说法正确，符合题意；
C、灯塔1在轮船的北偏西方向40千米处，故原说法错误，不符合题意；
D、灯塔2在轮船的北偏东方向30千米处，故原说法错误，不符合题意；
故选：B．
11．B
【分析】根据圆锥、圆柱、四棱柱、圆台的形状特点逐项判断即可得．
【详解】解：沿着与圆柱底面垂直的方向可以截出长方形，故符合题意；
圆锥中不可能截出长方形，故不合题意；
沿着与四棱柱任意一个面平行的方向可以截出长方形，故符合题意；
圆台中无法截出长方形，故不合题意；
∴符合要求的图形有2个，
故选：B．
【点睛】此题主要考查了截一个几何体，明确截面的形状既与被截的几何体有关，还与截面的角度和方向有关是解题的关键．
12．D
【分析】根据题意，找到规律，利用规律即可求解．
【详解】解：根据规律：正方形数可以用代数式表示为：（n+1）2，
两个三角形数分别表示为n（n+1）和（n+1）（n+2），
只有D、49=21+28符合，
故选D．
【点睛】此题考查了数字规律探索问题，解题的关键是根据题意，找到规律．
13．10
【分析】用最高温度减去最低温度，再根据减去一个数等于加上这个数的相反数进行计算即可得解．
【详解】解：，
故答案为：10．
【点睛】本题考查了有理数的减法的应用，熟记减去一个数等于加上这个数的相反数是解题的关键．
14．
【分析】本题考查代数式求值，先求得，再利用整体代入法求解即可．
【详解】解：，
，
，
故答案为：．
15．1
【分析】本题考查绝对值和平方式的非负性、代数式求值，根据非负数的性质求得a、b值即可求解．
【详解】解：，，
，，
，，
，
故答案为：1．
16．/156度
【分析】根据对顶角相等得到，利用角平分线的性质求出的度数，再根据邻补角求出，利用角的和，即可解答．
【详解】解：根据对顶角相等，得：，
射线平分，
，
，
，
故答案为：．
【点睛】本题考查对顶角和邻补角，角平分线的定义，解决本题的关键是熟记对顶角和邻补角的定义．
17．（1）7，（2）-12．
【分析】（1）按照有理数混合运算的顺序和法则计算即可；
（2）按照有理数混合运算的顺序和法则计算即可．
【详解】解：（1）
=
=8-1
=7
（2）
=
=
=-12．
【点睛】本题考查了有理数的混合运算，解题关键是熟练运用有理数的运算法则，按照有理数混合运算顺序进行计算．
18．(1)
(2)
【分析】（1）直接移项合并同类项求解即可；
（2）先去分母，然后去括号、移项、合并同类项求解即可．
【详解】（1）解：
；
（2）
．
【点睛】题目主要考查解一元一次方程的方法步骤，熟练掌握解一元一次方程的方法是解题关键．
19．，3
【分析】直接利用去括号法则以及合并同类项法则分别化简，再把已知数据代入得出答案．
【详解】解：原式
当，时
原式
【点睛】此题主要考查了整式的加减——化简求值，正确合并同类项和去括号是解题关键．
20．（1）4；（2）；（3）DE的长等于AC的长．
【分析】（1）先求出AB长，再根据线段的中点求出AD和BE长，即可求出答案；
（2）先求出AB长，再根据线段的中点求出AD和BE长，即可求出答案；
（3）根据（1）和（2）中的结果得出即可．
【详解】（1）∵AC=8，BC=6，∴AB=14．
∵点D是线段AB的中点，∴ADAB=7．
∵BC=6，点E是线段BC的中点，∴BEBC=3，∴DE=14﹣7﹣3=4；
（2）∵AC=m，BC=n，∴AB=m+n．
∵点D是线段AB的中点，∴AD．
∵BC=n，点E是线段BC的中点，∴BE，∴DE=m+n；
（3）规律：DE的长等于的长．
【点睛】本题考查了求两点之间的距离，能根据求出的结果得出规律是解答此题的关键．
21．（1）92.16（2）（3.33x-38.5）（3）72立方米
【分析】（1）根据总价＝单价×数量，即可求出结论；
（2）根据表格的天然气价格即可列出代数式；
（3）设张老师家11月份用了x立方米的天然气，根据题意列出一元一次方程即可求解．
【详解】（1）张老师家9月份使用天然气36立方米，则需缴纳天然气费为36×2.56=92.16（元）
故答案为：92.16；
（2）张老师家10月份使用天然气立方米，则需缴纳的天然气费为50×2.56+（x-50）×3.33=128+3.33x-166.5=3.33x-38.5(元)
故答案为：（3.33x-38.5）；
（3）设张老师家11月份用了x立方米的天然气，
∵缴纳天然气费201.26＞128
∴x＞50
∴3.33x-38.5=201.26，
解得：x＝72．
答：张老师家11月份使用天然气72立方米．
【点睛】本题考查了一元一次方程的应用，找准等量关系，正确列出一元一次方程是解题的关键．
22．(1)
(2)，理由见解析
(3)，理由见解析
【分析】（1）由余角性质和平行线的性质分析即可；
（2）过点B作，然后运用余角性质和平行线的性质解答即可；
（3）运用对顶角性质、余角性质和平行线的性质解答即可．
【详解】（1）解：设三角板与直线b的交点为N，
由余角性质和平行线的性质可知，
，
，
∴，
∴．
故答案为：．
（2）与的关系：．
证明：过点B作，
∵，．
∴
由题意可知，
，
∵
∴，
∵，
∴，
∴．
（3）．
证明：设与直线b交于E点，与直线b交于F点，
则，，，
∵，
∴，
∴．
【点睛】本题主要考查了对顶角的性质、余角的性质、平行线的性质等知识点，灵活使用平行线的性质是解答本题的关键．