2023-2024学年河南省南阳市唐河县八年级（上）期末数学试卷（含解析）

这是一份2023-2024学年河南省南阳市唐河县八年级（上）期末数学试卷（含解析），共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.16的立方根是( )
A. 8B. 4C. 316D. ±316
2.下列各式计算正确的是( )
A. (−a2b)3=a6b3B. (a−1)2=a2−1
C. a⋅a3+a4=2a4D. 2b(4a−1)=8ab+2b
3.估算 27+2的值是在( )
A. 5和6之间B. 6和7之间C. 7和8之间D. 8和9之间
4.如图，甲、乙、丙三个三角形和左侧△ABC全等的是( )
A. 甲和乙B. 甲和丙C. 乙和丙D. 只有丙
5.A、B、C三名同学玩“抢凳子”游戏．他们所站的位围成一个△ABC，在他们中间放一个木凳，谁先抢到凳子谁获胜，为保证游戏公平，则凳子应放的最适当的位置是在△ABC的( )
A. 三边垂直平分线的交点B. 三边中线的交点
C. 三个内角角平分线的交点D. 三边高的交点
6.五根小木棒，其长度分别为7，15，20，24，25，现将它们摆成两个直角三角形，如图，其中正确的是( )
A. B.
C. D.
7.乐乐爸爸的公司今年1−7月份的销售额在七个月之内增长率的变化状况如图所示．从图上看出，下列结论正确的是( )
A. 1−6月份销售额在逐渐减少B. 在这七个月中，1月份的销售额最大
C. 这七个月中，每月的销售额不断上涨D. 这七个月中，销售额有增有减
8.如图，在△ABC中，以点A为圆心，AC的长为半径作弧，与BC交于点E，分别以点E和点C为圆心、大于12EC的长为半径作弧，两弧相交于点P，作射线AP交BC于点D.若∠B=45°，∠C=2∠CAD，则∠BAE的度数为( )
A. 15°
B. 25°
C. 30°
D. 35°
9.如图，在边长为2a的正方形中央剪去一边长为(a+2)的小正方形(a>2)，将剩余部分剪开，密铺成一个平行四边形，则该平行四边形的面积为( )
A. 3a2−4B. 2a2+4aC. 3a2−4a−4D. 3a2+4a+4
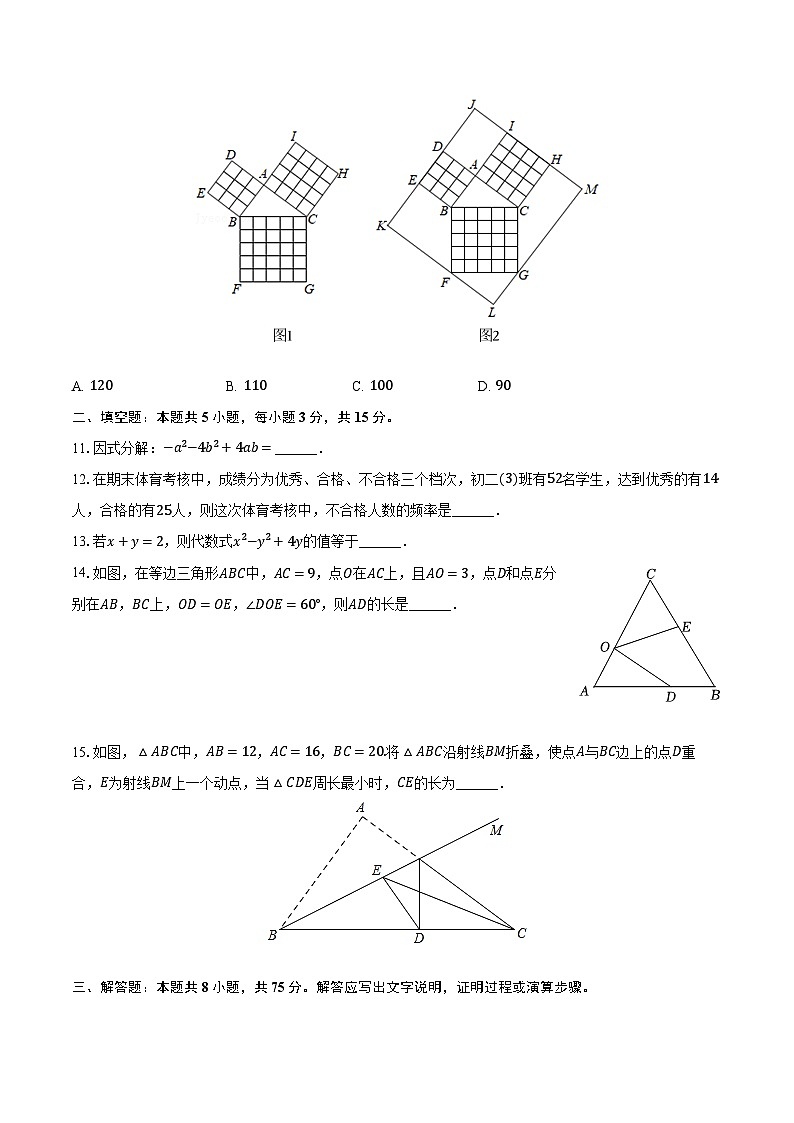
10.勾股定理在平面几何中有着不可替代的重要地位，在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载.如图1是由边长均为1的小正方形和Rt△ABC构成的，可以用其面积关系验证勾股定理.将图1按图2所示“嵌入”长方形LMJK，则该长方形的面积为( )
A. 120B. 110C. 100D. 90
二、填空题：本题共5小题，每小题3分，共15分。
11.因式分解：−a2−4b2+4ab=______．
12.在期末体育考核中，成绩分为优秀、合格、不合格三个档次，初二(3)班有52名学生，达到优秀的有14人，合格的有25人，则这次体育考核中，不合格人数的频率是______．
13.若x+y=2，则代数式x2−y2+4y的值等于______．
14.如图，在等边三角形ABC中，AC=9，点O在AC上，且AO=3，点D和点E分别在AB，BC上，OD=OE，∠DOE=60°，则AD的长是______．
15.如图，△ABC中，AB=12，AC=16，BC=20.将△ABC沿射线BM折叠，使点A与BC边上的点D重合，E为射线BM上一个动点，当△CDE周长最小时，CE的长为______．
三、解答题：本题共8小题，共75分。解答应写出文字说明，证明过程或演算步骤。
16.(本小题8分)
计算：
(1) (−2)2−3−338−| 3−2|；
(2)20232−2022×2024．
17.(本小题10分)
(1)化简：(2x−y)2−(x−2y)(x+2y)+(6x2y+8xy2)÷2y；
(2)已知x是 7的整数部分，y是 7的小数部分，求(y− 7)x+2的平方根．
18.(本小题9分)
如图，在四边形ABCD中，∠ABC=90°，CA平分∠BCD，且CA=CD，过点D作DE⊥AC于点E．
(1)求证：CB=CE；
(2)若AB=2，BC=1.5，求AD的长．
19.(本小题8分)
对垃圾进行分类投放，能有效提高对垃圾的处理和再利用，减少污染，保护环境，为了调查同学们对垃圾分类知识的了解程度，增强同学们的环保意识，普及垃圾分类及投放的相关知识，某校数学兴趣小组的同学设计了“垃圾分类知识及投放情况”问卷，并在本校随机抽取部分同学进行问卷测试，把测试成绩分成“优、良、中、差”四个等级，绘制了如图不完整的统计图：

根据以上统计信息，解答下列问题：
(1)求成绩是“优”的人数占抽取人数的百分比；
(2)求本次随机抽取问卷测试的人数；
(3)请把条形统计图补充完整；
(4)扇形统计图中成绩是“良”的圆心角的度数是______°.
20.(本小题10分)
如图，四边形ABCD为某工厂的平面图，经测量AB=BC=AD=80m，CD=80 3m，且∠ABC=90°．
(1)求∠DAB的度数；
(2)若直线AB为工厂的车辆进出口道路(道路的宽度忽略不计)，工作人员想要在点D处安装一个摄像头观察车辆进出工厂的情况，已知摄像头能监控的最远距离为80m，求被监控到的道路长度为多少m？
21.(本小题10分)
阅读与思考：下面是小宇同学的数学日记，请仔细阅读并完成相应的任务．
任务：
(1)请你补全小宇日记中不完整的部分：① ______，② ______；
(2)尺规作图：在图2中作∠CAB的角平分线，交BC于点D(保留作图痕迹，不写作法)；
(3)在(2)的条件下，直接写出线段CD的长度．
22.(本小题10分)
数形结合是一种重要的数学思想方法，利用图1中边长分别为a、b的两个正方形纸片和长为a、宽为b的长方形纸片，可以拼出一些图形来解释某些等式，如：由图2可得(a+b)(2a+b)=2a2+3ab+b2，则：

(1)由图3可以解释的等式是______；
(2)用9张边长为a的正方形纸片，12张长为b、宽为a的长方形纸片，4张边长为b的正方形纸片拼成一个大正方形，则这个大正方形的边长为______；
(3)先计算(a+2b)(2a−b)，再用图形的面积解释它的正确性．
23.(本小题10分)
已知：∠AOB=60°.小新在学习了角平分线的知识后，做了一个夹角为120°(即∠DPE=120°)的角尺来作∠AOB的角平分线．
(1)如图1，他先在边OA和OB上分别取OD=OE，再移动角尺使PD=PE，然后他就说射线OP是∠AOB的角平分线．试根据小新的做法证明射线OP是∠AOB的角平分线；
(2)如图2，小新在确认射线OP是∠AOB的角平分线后，一时兴起，将角尺绕点P旋转了一定的角度，他认为旋转后的线段PD和PE仍然相等．请问小新的观点是否正确，为什么？
(3)如图3，在(2)的基础上，若角尺旋转后恰好使得DP/​/OB，请判断线段OD与OE的数量关系，并说明理由．
答案和解析
1.【答案】C
【解析】解：∵(316)3=16，
∴16的立方根是316，
故选：C．
根据立方根的定义即可求解．
本题主要考查了立方根，掌握立方根的定义是解题的关键．
2.【答案】C
【解析】解：A.(−a2b)3=−a6b3，故本选项不符合题意；
B.(a−1)2=a2−2a+1，故本选项不符合题意；
C.a⋅a3+a4=2a4，故本选项符合题意；
D.2b(4a−1)=8ab−2b，故本选项不符合题意．
故选：C．
选项A根据积的乘方运算法则判断即可；选项B根据完全平方公式判断即可；选项C根据同底数幂的乘法法则以及合并同类项法则判断即可；选项D根据单项式乘多项式的运算法则判断即可．
本题考查了整式的混合运算，掌握相关运算法则是解答本题的关键．
3.【答案】C
【解析】解：因为 25< 27< 36，
所以5< 27<6，
所以 27+2的值是在：7和8之间．
故选：C．
首先得出 27的取值范围，进而得出答案．
此题主要考查了估算无理数的大小，正确得出最接近的有理数是解题关键．
4.【答案】C
【解析】解：根据SAS可以判断△ABC与乙中的三角形全等．
根据AAS或ASA可以判断△ABC与乙中的三角形全等．
故选：C．
利用全等三角形的判定方法一一判断即可．
本题考查全等三角形的判定，解题的关键是掌握全等三角形的判定，属于中考常考题型．
5.【答案】A
【解析】解：利用线段垂直平分线的性质得：三角形三边垂直平分线的交点到三个顶点距离相等，所以要放在三边垂直平分线的交点上．
故选：A．
为使游戏公平，要使凳子到三个人的距离相等，于是利用线段垂直平分线上的点到线段两端的距离相等可知，要放在三边垂直平分线的交点上．
本题主要考查了线段垂直平分线的性质的应用，利用所学的数学知识解决实际问题是一种能力，要注意培养．想到要使凳子到三个人的距离相等是正确解答本题的关键．
6.【答案】C
【解析】解：A、72+242=252，152+202≠242，故A不正确；
B、72+242=252，152+202≠242，故B不正确；
C、72+242=252，152+202=252，故C正确；
D、72+202≠252，242+152≠252，故D不正确．
故选：C．
欲求证是否为直角三角形，这里给出三边的长，只要验证两小边的平方和等于最长边的平方即可．
本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．勾股定理的逆定理：若三角形三边满足a2+b2=c2，那么这个三角形是直角三角形．
7.【答案】C
【解析】解：由折线统计图可知，1～7月份销售额的增长率始终是正数，即1−7月份销售额在增加，故选项A、B、D不合题意；
这七个月中，每月的销售额不断上涨，C说法正确，故本选项符合题意．
故选：C．
这七个月中，销售额的增长率始终是正数，则每月的销售额不断上涨，据此即可判断．
本题考查折线统计图的运用，折线统计图表示的是事物的变化情况，注意在图形中纵轴表示的是增长率，只有增长率是负数，才表示销售额减少．
8.【答案】A
【解析】解：由题意可知，AP是EC的垂直平分线，
∴AD⊥BC，DE=CD，
∴△ADE≌△ADC(SAS)，
∴∠EAD=∠CAD，∠C=∠AED，
∴∠EAC=2∠CAD，
∵∠C=2∠CAD，
∴∠C=∠EAC=∠AED，
∴△AEC是等边三角形，
∴∠C=∠EAC=∠AED=60°，
在△ABC中，∠B=45°，∠C=60°，
∴∠BAC=180°−45°−60°=75°，
∴∠BAE=75°−60°=15°．
故选：A．
由题意可知，AP是EC的垂直平分线，证明△ADE≌△ADC(SAS)，进而证明△AEC是等边三角形，求出∠C=∠EAC=∠AED=60°，利用三角形内角和定理即可求解．
本题考查了全等三角形的性质与判定，等边三角形的性质与判定，三角形内角和定理，熟练掌握等边三角形的性质与判定是解题的关键．
9.【答案】C
【解析】解：该平行四边形的面积为(2a)2−(a+2)2=4a2−a2−4a−4=3a2−4a−4，
故选：C．
直接用大正方形的面积，减去小正方形的面积，进行计算即可．
本题考查了平方差公式的几何背景，根据拼接前后的图形的面积相等列式是解题的关键．
10.【答案】B
【解析】解：延长AB交KL于点O，延长AC交LM于点P，如图2所示：
则四边形AOLP是矩形，
∴∠BOF=∠BAC=90°，
∵四边形BCGF是正方形，
∴BC=BF，∠CBF=90°，
∴∠ABC+∠OBF=90°，
又∵Rt△ABC中，∠ABC+∠ACB=90°，
∴∠OBF=∠ACB，
在△OBF和△ACB中，
∠BAC=∠BOF∠ACB=∠OBFBC=BF，
∴△OBF≌△ACB(AAS)，
∴AC=OB，
同理：△ACB≌△PGC(AAS)，
∴PC=AB，
∴AB+OB=PC+AC，
即OA=AP，
∴矩形AOLP是正方形，边长AO=AB+OB=AB+AC=3+4=7，
∴KL=3+7=10，LM=4+7=11，
∴长方形LMJK的面积为：10×11=110，
故选：B．
延长AB交KL于点O，延长AC交LM于点P，证△OBF≌△ACB(AAS)，得AC=OB，同理△ACB≌△PGC(AAS)，得PC=AB，再证矩形AOLP是正方形，边长AO=7，则KL=10，LM=11，即可解决问题．
本题考查了勾股定理、矩形的性质、正方形的判定与性质、全等三角形的判定与性质等知识，正确作出辅助线构造三角形全等是解题的关键．
11.【答案】−(a−2b)2
【解析】解：原式=−(a2−4ab+4b2)
=−(a−2b)2．
故答案为：−(a−2b)2．
先提取“−”号，再根据完全平方公式分解因式即可得出答案．
本题考查了因式分解−运用公式法，掌握a2±2ab+b2=(a±b)2是解题的关键．
12.【答案】0.25
【解析】解：根据题意，不合格人数为52−14−25=13，
∴不合格人数的频率是13÷52=0.25，
故答案为：0.25．
先求出不合格人数，再根据频率计算公式：频率=频数÷总数求解即可．
本题考查频率，熟记频率计算公式是解题关键．
13.【答案】4
【解析】解：∵x+y=2，
∴x2−y2+4y=(x+y)(x−y)+4y
=2(x−y)+4y
=2x−2y+4y
=2x+2y
=2(x+y)
=2×2
=4，
故答案为：4．
先根据平方差公式进行计算，再代入求出即可．
本题考查了平方差公式，能熟记公式是解此题的关键，注意：(a+b)(a−b)=a2−b2．
14.【答案】6
【解析】解：∵AC=9，点O在AC上，AO=3，
∴CO=AC−AO=9−3=6，
∵△ABC是等边三角形，
∴∠A=∠C=60°，
∴∠ADO=180°−∠A−∠AOD=120°−∠AOD，
∵∠DOE=60°，
∴∠COE=180°−∠DOE−∠AOD=120°−∠AOD，
∴∠ADO=∠COE，
在△ADO和△COE中，
∠ADO=∠COE∠A=∠COD=OE，
∴△ADO≌△COE(AAS)，
∴AD=CO=6，
故答案为6．
由AC=9，AO=3，得CO=6，由等边三角形的性质得∠A=∠C=60°，而∠DOE=60°，可推导出∠ADO=∠COE=120°−∠AOD，因为OD=OE，所以△ADO≌△COE，则AD=CO=6，于是得到问题的答案．
此题重点考查等边三角形的判定与性质、三角形内角和定理、全等三角形的判定与性质等知识，证明△ADO≌△COE是解题的关键．
15.【答案】10
【解析】解：由题意可知，A、D两点关于射线BM对称，
∴C△CDE=CD+DE+CE，
∵CD为定值，
要使△CDE周长最小，即DE+CE最小，
∴AC与射线BM的交点，即为使△CDE周长最小的点E，
∵AB=12，AC=16，BC=20.且122+162=202，
∴AB2+AC2=BC2，
∴△ABC为直角三角形，
∴∠BAC=∠BDE=∠CDE=90°，
∵AB=BD=12，
∴CD=BC−BD=8，
设CE=x，则AE=DE=16−x，
Rt△CDE中，CE2=DE2+CD2，
即x2=(16−x)2+82，
∴x=10，
∴CE=10．
故答案为：10．
根据翻折的性质及勾股定理的逆定理可得△ABC为直角三角形，设CE=x，则AE=DE=16−x，然后再由勾股定理可得答案．
此题考查的是翻折变换、勾股定理的逆定理及轴对称性质，掌握其性质是解决此题关键．
16.【答案】解：(1)原式=2−(−32)−(2− 3)
=2+32−2+ 3
=3+2 32；
(2)原式=20232−(2023−1)(2023+1)
=20232−20232+1
=1．
【解析】(1)根据算术平方根，立方根以及绝对值的定义进行计算即可；
(2)根据平方差公式进行计算即可．
本题考查平方差公式，实数的运算，掌握平方差公式的结构特征以及绝对值的定义是正确解答的关键．
17.【答案】解：(1)(2x−y)2−(x−2y)(x+2y)+(6x2y+8xy2)÷2y
=4x2−4xy+y2−x2+4y2+3x2+4xy
=6x2+5y2；
(2)∵x是 7的整数部分，y是 7的小数部分，
∴x=2，y= 7−2，
∴± (y− 7)x+2
=± ( 7−2− 7)2+2
=± (−2)4
=±4，
即(y− 7)x+2的平方根是±4．
【解析】(1)根据完全平方公式、平方差公式和多项式除以单项式将题目中的式子展开，然后合并同类项即可；
(2)根据x是 7的整数部分，y是 7的小数部分，可以得到x=2，y= 7−2，然后即可求得(y− 7)x+2的平方根．
本题考查整式的混合运算、二次根式的混合运算，熟练掌握运算法则是解答本题的关键，注意平方差公式和完全平方公式的应用．
18.【答案】(1)证明：∵CA平分∠BCD，
∴∠ACB=∠DCE，
∵DE⊥AC，
∴∠DEC=∠DEA=90°，
∵∠ABC=90°，
∴∠ABC=∠DEC，
在△ABC和△DEC中，
∠ABC=∠DEC∠ACB=∠DCECA=CD，
∴△ABC≌△DEC(AAS)，
∴CB=CE；
(2)解：由(1)知△ABC≌△DEC，
∴CB=CE，AB=DE，
∵AB=2，BC=1.5，
∴CE=1.5，DE=2，
在Rt△ABC中，由勾股定理得AC= AB2+BC2= 22+1.52=2.5，
∴AE=AC−CE=2.5−1.5=1，
在Rt△DEA中，由勾股定理得AD= AE2+DE2= 12+22= 5．
【解析】(1)根据AAS证得△ABC和△DEC全等即可；
(2)由△ABC≌△DEC得CB=CE=1.5，AB=DE=2，由勾股定理求出AC的长，即可求出AE的长，在Rt△DEA中由勾股定理即可求出AD的长．
本题考查了全等三角形的判定与性质，角平分线的定义，勾股定理，解题的关键是掌握全等三角形的判定定理．
19.【答案】126
【解析】解：(1)72°÷360°=20%，
即“优”的人数占抽取人数的百分比为20%；
(2)40÷20%=200(人)，
即抽取检测的人数为200人；
(3)“中”的人数为：200−40−70−30=60(人)，
画图如下：
(4)扇形统计图中成绩是“良”的圆心角的度数是360°×70200=126°，
故答案为：126．
(1)根据“优”所对的圆心角度数除以360°即可求解；
(2)用“优”的人数除以其所占比例即可求解；
(3)用总人数减去“优”、“良”、“差”的人数即可求出“中”的人数，据此画图即可；
(4)总人数乘以“良”的人数和所占的比例即可．
本题考查了条形统计图和扇形统计图，求扇形圆心角度数和画条形统计图的知识．根据“优”所对的圆心角度数求出该项人数所占比例是解答本题的关键．
20.【答案】解：(1)连接AC，
∵AB=BC=AD=80m，∠ABC=90°
∴△ABC是等腰直角三角形，
∴AC= AB2+BC2= 802+802=80 2(m)，∠CAB=45°，
∵CD=80 3m，
在△ACD中，AD2+AC2=802+(80 2)2=(80 3)2=CD2，
∴△ACD是直角三角形，
∴∠CAD=90°，
∴∠DAB=90°+45°=135°；
(2)过点D作DE⊥AB于E，作点A关于DE的对称点F，连接DF，
由轴对称的性质，得：DF=DA=80m，AE=EF，
由(1)知，∠BAD=135°，
∴∠DAE=45°，
∴△ADE是等腰直角三角形，
∴AE=DE= 22AD=40 2(m)，
∴AF=2AE=80 2(m)，
∴被监控到的道路长度为80 2m.
【解析】(1)根据等腰直角三角形的性质得出AC，进而利用勾股定理逆定理解答即可；
(2)根据轴对称的性质和勾股定理解答即可．
本题考查了勾股定理的应用、勾股定理的逆定理、轴对称的性质以及等腰直角三角形的判定与性质等知识，熟练掌握勾股定理和勾股定理的逆定理是解题的关键．
21.【答案】(a+b)2=a2+2ab+b2 125 (a+b)2=a2+2ab+b2 125
【解析】解：(1)补全小宇日记中不完整的部分：①(a+b)2=a2+2ab+b2，
②点C到AB的距离为3×45=125，
故答案为：(a+b)2=a2+2ab+b2，②125；
(2)如图所示，线段AD即为所求；
(3)过D作DE⊥AB于E，
∵AD平分∠BAC，∠C=90°，
∴CD=DE，
∵AD=AD，
∴Rt△ACD≌Rt△AED(HL)，
∴AE=AC=3，
∴BE=2，
∵DE2+BE2=BD2，
∴CD2+22=(4−CD)2，
∴CD=32，
故线段CD的长度为32．
(1)①根据完全平方公式即可得到结论；②根据三角形的面积公式即可得到结论；
(2)根据角平分线的作法作出图形即可；
(3)过D作DE⊥AB于E，根据角平分线的性质得到CD=DE，根据全等三角形的判定和性质得到AE=AC=3，根据勾股定理即可得到结论．
本题考查了作图−基本作图，完全平方公式，三角形的面积公式，勾股定理，全等三角形的判定和性质，正确地作出图形是解题的关键．
22.【答案】(a+b)2=(a−b)2+4ab 3a+2b
【解析】解：(1)∵从整体看，大正方形的边长为a+b，
∴大正方形的面积为：(a+b)2；
∵组成看，大正方形由一个小正方形和四个长方形组成，
∴大正方形的面积为：(a−b)2+4ab．
∴(a+b)2=(a−b)2+4ab．
故答案为：(a+b)2=(a−b)2+4ab；
(2)∵大正方形的面积为：9a2+12ab+4b2=(3a+2b)2，
∴大正方形的边长为：3a+2b；
(3)(a+2b)(2a−b)=2a2−ab+4ab−2b2=2a2+3ab−2b2；
如图：四边形ABCD的面积即可表示：(a+2b)(2a−b)的计算结果．
(1)从整体看，大正方形的边长为a+b，那么可表示出大正方形的面积为：(a+b)2；从组成看，大正方形由一个小正方形和四个长方形组成，可表示为：(a−b)2+4ab，让它们相等即可；
(2)易得大正方形的面积为9a2+12ab+4b2，符合完全平方公式，可表示为(3a+2b)2，那么边长为：3a+2b；
(3)用第一个括号里的每一项，去乘另一个括号里的每一项，最后把所得的积相加即可；根据(1)、(2)可得图形从整体看边长为：(a+2b)和(2a−b)，从组成看：由2a2，ab，4ab，−2b2组成，画出相关图形即可．
本题考查完全平方式及其应用．根据图形中面积的不同表示方法得到相关等式是解决本题的关键．用到的知识点为：a2+2ab+b2=(a+b)2．
23.【答案】(1)证明：如图1中，

在△OPD和△OPE中，
OD=OEPD=PEOP=OP，
∴△OPD≌△OPE(SSS)，
∴∠POD=∠POE．
(2)解：结论正确．
理由：如图2中，过点P作PH⊥OA于H，PK⊥OB于K．

∵∠PHO=∠PKO=90°，∠AOB=60°，
∴∠HPK=120°，
∵∠DPE=∠HPK=120°，
∴∠DPH=∠EPK，
∵OP平分∠AOB，PH⊥OA，PK⊥OB，
∴∠POH=∠POK，∠PHO=∠PKO=90°，
在△OPH和△OPK中，
∠POH=∠POK∠PHO=∠PKO=90°OP=OP，
∴△OPH≌△OPK(AAS)，
∴PH=PK，
在△PHD和△PKE中，
∠PHD=∠PKEPH=PK∠DPH=∠EPK，
∴△PHD≌△PKE(ASA)，
∴PD=PE．
(3)解：结论：OE=2OD．
理由：如图3中，在OB上取一点T，使得OT=OD，连接PT．

∵OP平分∠AOB，
∴∠POD=∠POT，
在△POD和△POT中，
OD=OT∠POD=∠POTOP=OP，
∴△POD≌△POT(SAS)，
∴∠ODP=∠OTP，
∵PD/​/OB，
∴∠PDO+∠AOB=180°，∠DPE+∠PEO=180°，
∵∠AOB=60°，∠DPE=120°，
∴∠ODP=120°，∠PEO=60°，
∴∠OTP=∠ODP=120°，
∴∠PTE=60°，
∴∠TPE=∠PET=60°，
∴TP=TE，
∵∠PTE=∠TOP+∠TPO，∠POT=30°，
∴∠TOP=∠TPO=30°，
∴OT=TP，
∴OT=TE，
∴OE=2OD．
【解析】(1)根据SSS证明△OPD≌△OPE(SSS)，可得结论．
(2)结论正确．如图2中，过点P作PH⊥OA于H，PK⊥OB于K.证明△PHD≌△PKE(ASA)，可得结论．
(3)结论：OE=2OD.如图3中，在OB上取一点T，使得OT=OD，连接PT.想办法证明PT=OT，PT=TE，可得结论．
本题属于几何变换综合题，考查了全等三角形的判定和性质，角平分线的判定等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．×年×月×日星期日
用等面积法解决问题
周末，我对本学期所学的内容进行了回顾与整理，发现数学中有许多方法是可以互相迁移的．
比如我们在学习整式乘法时，借助如图Ⅰ所示的边长为(a+b)的正方形，用两种不同的方法表示这个正方形的面积，可以得到乘法公式______①.
再比如学习三角形的内容时，我遇到了同样可以用等面积法解决的问题.如图2，在Rt△ABC中，∠C=90°，AC=3，BC=4，AB=5，求点C到AB的距离.我们也可以利用等面积法求得点C到AB的距离为______②.
总结：等面积法是一种重要的数学解题方法，在解题中，灵活运用等面积法解决相关问题，不仅可以使解题思路清晰，过程简洁，而且还能体现知识间的相互联系．