八年级下册17.4 一元二次方程的根与系数的关系课堂教学课件ppt

这是一份八年级下册17.4 一元二次方程的根与系数的关系课堂教学课件ppt，共15页。PPT课件主要包含了学习目标，新课导入，概念剖析，填一填，能证明你的猜想吗，x1x2，证一证，典型例题，当堂检测，两数之和为0等内容，欢迎下载使用。

1.熟知一元二次方程的根与系数的关系2.会运用根与系数的关系解决有关问题（重点）
一元二次方程ax2+bx+c=0(a≠0)通过什么来判断方程根的情况？判别式(=b2-4ac)，>0，方程有两个不等实根；=0，方程有两个相等实根；<0，方程没有实数根.
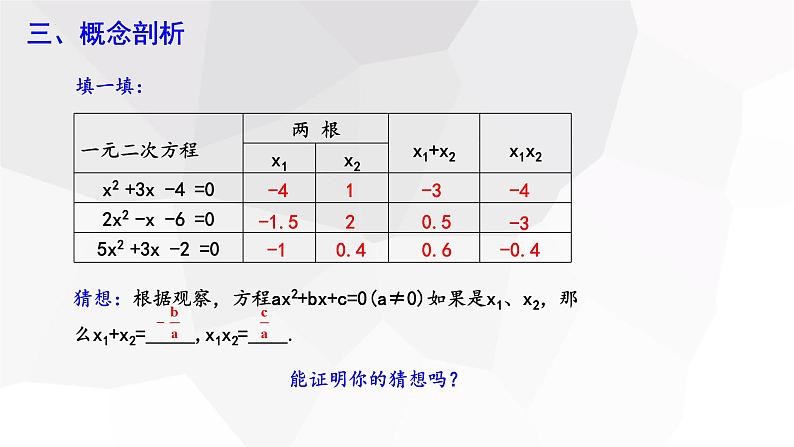
思考：若方程有实数根x1,x2，写出x1,x2的值，那么x1+x2,x1x2和a、b、c有什么关系？
猜想：根据观察，方程ax2+bx+c=0(a≠0)如果是x1、x2，那么x1+x2= ,x1x2= .
韦达定理：如果ax2+bx+c=0(a≠0)的两个根分别是x1、x2，那么x1+x2= ,
例1.小明某天的作业如下：(1)x2+2x-12=8x+3 ，则x1+x2=(-2) ,x1x2=(-12) (2)x2-2x+3=0,则x1+x2=(2) ,x1x2=(3)(3)3x2+7x-9=0,则x1+x2=(7) ,x1x2=(-9)小明的答案是否正确？若错误，写出正确答案.
提示：对于ax2+bx+c=0 (a0，≥0)，x1+x2= ,x1x2=
解：(1)方程化为一般式：x2-6x-15=0=b2-4ac=(-6)2-4×1×(-15)=96>0故方程有两个不相等根∴x1+x2=6 ,x1x2=-15∴(1)答案错误
x1+x2=6 ,x1x2=-15
(2)x2-2x+3=0,则x1+x2=(2) ,x1x2=(3)
(2)=b2-4ac=(-2)2-4×1×3=-8<0故方程没有实数根∴不存在x1+x2,x1x2∴(2)答案错误
(3)=b2-4ac=72-4×2×(-8)=113>0故方程有两个不相等根∴x1+x2=-3.5,x1x2=-4∴(3)答案错误
(3)2x2+7x-8=0,则x1+x2=(3.5) ,x1x2=(-4)
不存在x1+x2,x1x2
1.在下列方程中，以3，-4为根的一元二次方程是（　　） A.x2-x-12=0 B.x2+x-12=0 C.x2-x+12=0 D.x2+x+12=0
2.判定下列各方程后面括号内的两个数是不是它的两个根.(1)x2+5x+4＝0(1,4);(2)x2-6x-7＝0(-1,7);(3)2x2-3x+1＝0(0.5,1);(4)3x2+5x-2＝0( ,2);(1)x2-8x+11＝0(3,5);
例2.一元二次方程x2(m1)x2m10,(1)求m满足什么条件时,方程的两根互为相反数？
解：(1)a=1，b=(m1)，c=2m1△=b2-4ac=[(m1)]2－4×1×(2m1)=m26m5∵两根互为相反数∴两根之和=m1=0,解得m1,此时△=m26m5=(-1)26×(-1)5=12>0,方程有两个不等根∴m1时,方程的两根互为相反数.
方程形如ax2+bx+c=0 (a0，≥0)，若两根互为相反数,则b=0
例2.一元二次方程x2(m1)x2m10,(2)求m满足什么条件时,方程的两根互为倒数？
(2)∵两根互为倒数 ∴两根之积=2m1=1 解得m1此时△=m26m5=126×15=0,方程有两个相等的根∴m1时,方程的两根互为倒数.
方程形如ax2+bx+c=0 (a0，≥0)，若两根互为倒数,则ac
例2.一元二次方程x2(m1)x2m10,(3)求m满足什么条件时,方程的一根为零？
(3)∵方程一根为0 ∴两根之积=2m1=0 解得m0.5此时△=m26m5=(0.5)26×0.55=2.25>0,方程有两个不等根∴m0.5时,方程的一根为零
任何一个数与0相乘结果为0两根之积为0
方程形如ax2+bx+c=0 (a0，≥0)，若一根为0,则c=0
3.已知关于x的一元二次方程x2-(k+1)x-6=0的一个根是2，则此方程的另一个根和k的值分别是（　　） A.3和2 B.3和-2 C.-3和-2 D.2和3 4.若x的一元二次方程x2-(2m-1)x-6=0的两根互为相反数,则k .
5.已知关于x的一元二次方程x2-2x+m=0有两个不等实根，(1)求m的范围；(2)若两个实数根为x1,x2，且x1+2x2=6,求m的值.
解：(1)a＝1，b＝-2，c＝m△=b2-4ac=(-2)2－4×1×m＝4-4m依题有：△>0,即4-4m>0解得m<1
(2)根据韦达定理可知：x1+x2=2，x1x2=m∵解得x1=-2，x2=4∴m=x1x2=(-2)×4=-8-8<1,故m的值为-8