






湘教版九年级下册第3章 投影与视图3.2 直棱柱、圆锥的侧面展开图优质ppt课件
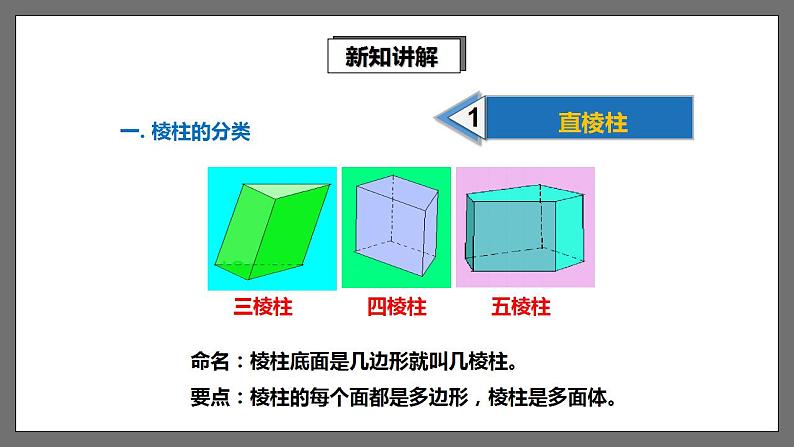
展开请仔细观察下列立体图形,它们有什么共同特点吗?
命名:棱柱底面是几边形就叫几棱柱。要点:棱柱的每个面都是多边形,棱柱是多面体。
斜棱柱:侧棱不垂直于底的棱柱叫做斜棱柱。
直棱柱:侧棱垂直于底的棱柱叫做直棱柱。
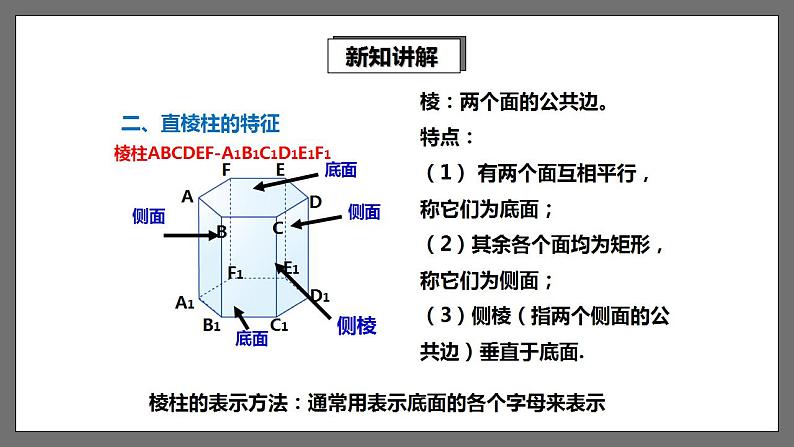
棱:两个面的公共边。特点:(1) 有两个面互相平行,称它们为底面;(2)其余各个面均为矩形,称它们为侧面;(3)侧棱(指两个侧面的公共边)垂直于底面.
棱柱的表示方法:通常用表示底面的各个字母来表示
棱柱ABCDEF-A1B1C1D1E1F1
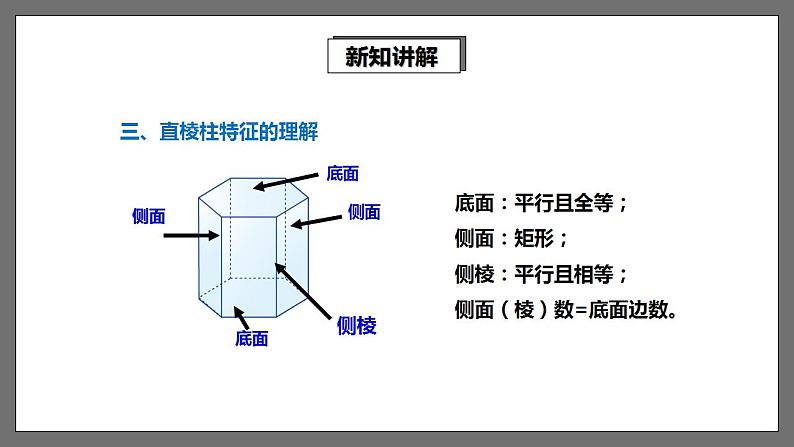
底面:平行且全等;侧面:矩形;侧棱:平行且相等;侧面(棱)数=底面边数。
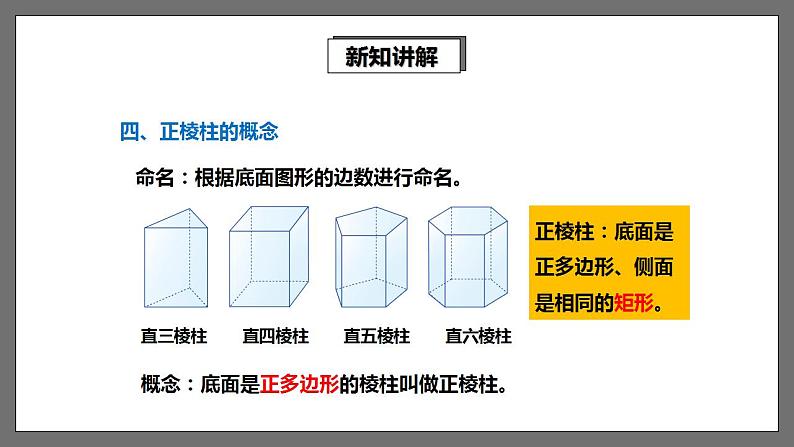
概念:底面是正多边形的棱柱叫做正棱柱。
命名:根据底面图形的边数进行命名。
正棱柱:底面是正多边形、侧面是相同的矩形。
收集几个直棱柱模型,再把侧面沿一条侧棱剪开,它们的侧面能否展开成平面图形,是矩形吗?
五、直棱柱的侧面展开图
直棱柱的侧面展开图是一个矩形,这个矩形的长是直棱柱的底面周长,宽是直棱柱的侧棱长(高)。
一个食品包装盒的侧面展开图如下图所示,它的底面是边长为2的正六边形,这个包装盒是什么形状的几何体?试根据已知数据求出它的侧面积。
解:根据图示可知该包装盒的侧面是矩形,又已知上、下底面是正六边形,因此这个几何体是正六棱柱(如图所示)。
由已知数据可知它的底面周长为2×6=12,因此它的侧面积为12×6=72。
1. 一个直棱柱有10个顶点,那么它面的个数是 。
解析:有10个顶点的直棱柱是五棱柱,所以它有7个面。
2. 下列说法错误的是( )若直棱柱的底面边长都相等,则它的各个侧面面积相等n棱柱有n个面,n个顶点长方体,正方体都是四棱柱三棱柱的底面是三角形
解析:n棱柱有n+2个面,n个顶点
3. 将如图所示的三棱柱展开,可以得到的图形是( )
解析:上底的直角三角形的斜边顶点与侧面的平行四边形的顶点重合。
圆锥:由一个底面和一个侧面围成的图形。底面是一个圆,侧面是一个曲面。
高:连接顶点与底面圆心的线段叫作圆锥的高。
母线:圆锥顶点与底面圆上任意一点的连线段都叫作圆锥的母线,母线长度均相等。
二、圆锥的高、半径和母线的关系
2. 侧面展开图扇形的半径 =母线的长PA
3.侧面展开图扇形的弧长 =底面周长
1. 圆锥的侧面展开图是扇形
四、圆锥的侧面积、底面积、表面积求解
表面积:(侧面积+底面积)
如图,小刚用一张半径为24cm的扇形纸板做一个圆锥形帽子(接缝忽略不计),如果做成的圆锥形帽子的底面半径为10cm,那么这张扇形纸板的面积S是多少?
分析:圆锥形帽子的底面周长就是扇形的弧长。
四、圆锥的圆心角与底面半径、母线的关系
当圆锥的轴截面是等边三角形时,圆锥的侧面展开图是一个半圆。
根据下列条件求圆锥侧面积展开图的圆心角(r、h、 a分别是圆锥的底面半径、高线、母线长)(结果保留一位小数)
1. h=3,r=4, 则 θ =__________
2. h=8,r=15 , 则 θ =__________
3. r=1, a=3 , 则 θ =__________
1. 如图,圆锥的顶点为P, AB是底面⊙O 的一条直径, ∠APB =90°,底面半径为r,求这个圆锥的侧面积和表面积。
2. 一个半径为4cm的圆形纸片,沿着直径剪成两个半圆,你能卷成两个圆锥吗?如果能,每个圆锥的底面面积是多少?
(2×3.14×4÷2)÷(2×3.14)=12.56÷6.28=2(cm)
3.14×2²=3.14×412.56(cm²)
答:能卷成两个圆锥,每个圆锥的底面面积为12.56cm²。
3. 如图是一个立方体纸盒的展开图,使展开图沿虚线折叠成正方体后相对面上的两个数互为相反数,求:a= ,b= ,c= 。
侧面积、底面积、表面积的求解方法
圆心角与底面半径、母线的关系
初中数学湘教版九年级下册第3章 投影与视图3.2 直棱柱、圆锥的侧面展开图习题课件ppt: 这是一份初中数学湘教版九年级下册第3章 投影与视图3.2 直棱柱、圆锥的侧面展开图习题课件ppt,共9页。
湘教版九年级下册第3章 投影与视图3.2 直棱柱、圆锥的侧面展开图习题ppt课件: 这是一份湘教版九年级下册第3章 投影与视图3.2 直棱柱、圆锥的侧面展开图习题ppt课件,共26页。
初中数学湘教版九年级下册3.2 直棱柱、圆锥的侧面展开图习题ppt课件: 这是一份初中数学湘教版九年级下册3.2 直棱柱、圆锥的侧面展开图习题ppt课件,共20页。













