九年级下册2.3 垂径定理精品课件ppt

这是一份九年级下册2.3 垂径定理精品课件ppt，文件包含湘教版数学九年级下册23《垂径定理》课件pptx、湘教版数学九年级下册23《垂径定理》教案doc等2份课件配套教学资源，其中PPT共33页， 欢迎下载使用。

1、圆是轴对称图形吗？它的对称轴是什么？你能找到多少条对称轴？
圆是轴对称图形，其对称轴是任意一条直径（过圆心的直线），圆有无数条对称轴．
2、1400多年前，我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形，它的跨度(弧所对的弦的长)为37.4 m，拱高(弧的中点到弦的距离，也叫弓形高)为7.2 m，求桥拱的半径(精确到0.1 m)．
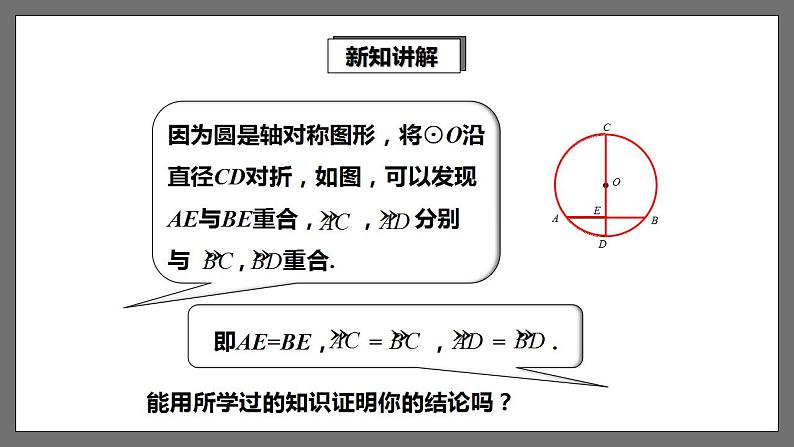
能用所学过的知识证明你的结论吗？
证明：如图，连接OA，OB．
∵ OA=OB，∴△OAB是等腰三角形．
∵OE⊥AB，∴AE=BE，∠AOD=∠BOD．
从而 ∠AOC=∠BOC．
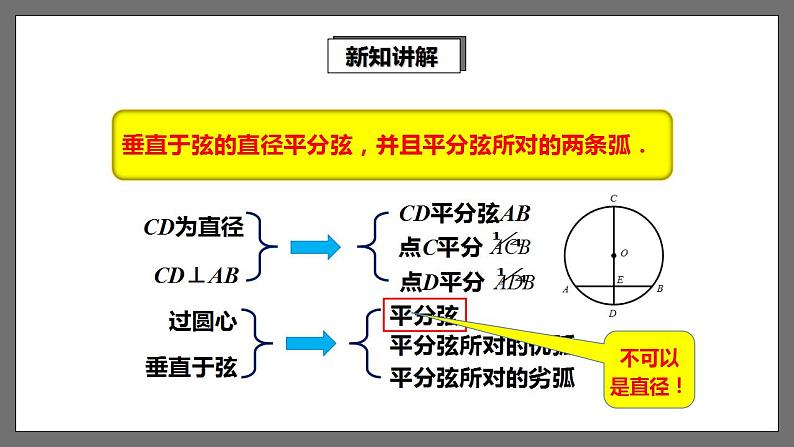
垂直于弦的直径平分弦，并且平分弦所对的两条弧．
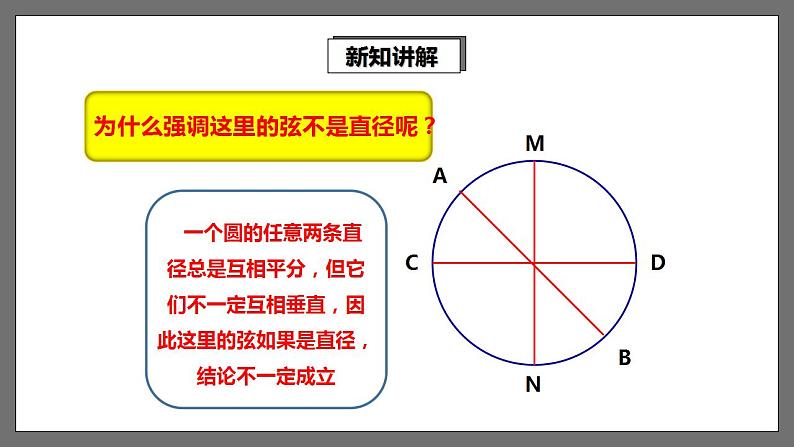
为什么强调这里的弦不是直径呢？
Y一个圆的任意两条直径总是互相平分，但它们不一定互相垂直，因此这里的弦如果是直径，结论不一定成立
下列图形是否具备垂径定理的条件？如果不是，请说明为什么？
不是，因为CD没有过圆心
垂径定理的几个基本图形：
如图，在下列五个条件中：①CD是直径；　　②CD⊥AB；　　③AM=BM；④ 　=　　；　 ⑤　　　　．只要具备其中两个条件，就可推出其余三个结论．你可以写出相应的命题吗？
已知：CD是直径，AB是弦，并且 = ．求证：CD平分AB，CD⊥AB， ．
（1）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧．
已知：CD是直径，AB是弦，并且 ．求证：CD平分AB，CD⊥AB， = ．
（2）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧．
已知：AB是弦，CD平分AB，CD⊥AB．求证：CD是直径， ， = ．
（3）弦的垂直平分线经过圆心，并且平分弦所对的两条弧．
（4）垂直于弦并且平分弦所对的一条弧的直径过圆心，并且平分弦所对的另一条弧．
（5）平分弦并且平分弦所对的一条弧的直径过圆心，垂直于弦，并且平分弦所对的另一条弧．
（6）平分弦所对的两条弧的直径过圆心，并且垂直平分弦．
例1 如图，弦AB=8 cm，CD是⊙O的直径，CD⊥AB，垂足为E，DE=2 cm，求⊙O的直径CD的长．
设OA=r cm，则OE=r-2（cm）．
在Rt△AEO中，根据勾股定理：OA2=OE2+AE2．即r2=(r-2)2+42．
∴CD=2r=10（cm）．
例2 证明：圆的两条平行弦所夹的弧相等．
已知：如图，在⊙O中，弦AB与弦CD平行．
证明：作直径EF⊥AB，
又∵AB∥CD，EF⊥AB，
求证：　　　 ．　　　　　
∴ ．
∴EF⊥CD， ∴ ．
因此 ，即　　　　．
垂径定理的推论2圆的两条平行弦所夹的弧相等．
垂径定理的推论2有这两种情况：
解决“赵州桥”的问题：
如图，OA=OC=R，OD=OC-CD=R-7.2，AB=18.7．
AD2+OD2=OA2．
即：18.72+(R-7.2)2=R2．
答：赵州桥的主桥拱半径约为27.9m．
在圆中有关弦长a，半径r， 弦心距d（圆心到弦的距离），弓形高h的计算题，常常通过连半径或作弦心距构造直角三角形，利用垂径定理和勾股定理求解．
应用垂径定理时辅助线的添加方法
弦a，弦心距d，弓形高h，半径r之间有以下关系：
d+h=r
1、半径为4 cm的⊙O中，弦AB=4 cm， 那么圆心O到弦AB的距离是________cm．2、⊙O的直径为10 cm，圆心O到弦AB的距离为3 cm，则弦AB的长是________cm．3、半径为2 cm的圆中，过半径中点且垂直于这条半径的弦长是________cm．
4、如图，已知AB为⊙O的直径，点D是弦AC的中点，BC=8 cm，求OD的长．
解：∵点O是AB的中点，点D是弦AC的中点，
∴OD是△ABC的中位线，
5、如图，⊙O的直径AB垂直弦CD于M，且M是半径OB的中点，CD=8 cm，求直径AB的长．
由勾股定理得：OC2=OM2+CM2，
6、如图，有一座拱桥是圆弧形，它的跨度AB=60米，拱高PD=18米．（1）求圆弧所在的圆的半径r的长；（2）当洪水泛滥到跨度只有30米时，要采取紧急措施，若拱顶离水面只有4米，即PE=4米时，是否要采取紧急措施？
在Rt△ADO中，由勾股定理得：r2=302+（r-18）2，
∴A′B′=32．∵A′B′=32＞30，∴不需要采取紧急措施．
∵OE=OP-PE=30，
∴在Rt△A′EO中，由勾股定理得：A′E2=A′O2-OE2，即：A′E2=342-302，
2、垂径定理：垂直于弦的直径平分弦，并且平分弦对的两条弧．
3、垂径定理的推论1：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．
4、垂径定理的推论2：垂直平分弦的直线过圆心，并且平分弦所对的两条弧．