陕西省汉中市宁强县2023-2024学年七年级上学期期末数学试题(含答案)

这是一份陕西省汉中市宁强县2023-2024学年七年级上学期期末数学试题(含答案)，共19页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。


一、单选题
1．下面四个数中，最小的数是（ ）．
A．2B．0C．D．
2．若数轴上的点表示，则与点相距5个单位长度的点表示的数是（ ）
A．3B．C．3或D．或7
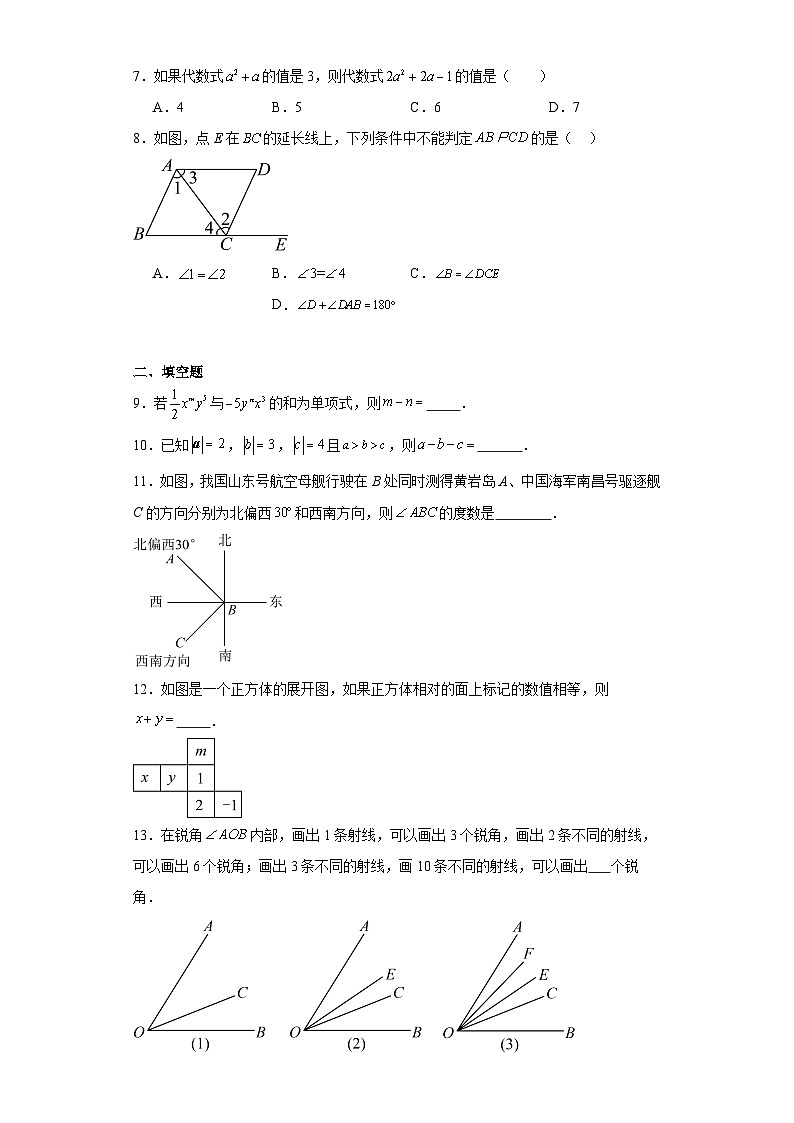
3．下列标注的图形名称与图形不相符的是（ ）
A．四棱锥B．圆柱C．四棱柱D．三棱锥
4．下列结论正确的是（ ）
A．精确到千位B．近似数精确到个位
C．近似数和近似数表示的意义相同D．近似数5万与近似数50000的精确度相同
5．下图是一组有规律的图案，第1个图案由4个基础图形组成，第2个图案由7个基础图形组成，第3个图案由10个基础图形组成，…，第9个图案中基础图形个数为（ ）
A．27B．28C．30D．36
6．下列现象：①用两根钉子就可以把一根木条固定在墙上；②把弯曲的公路改直，就能够缩短路程；③体育课上测量某个同学的跳远成绩；④工人砌墙时，先在两端立桩拉线，然后沿着线砌墙．其中，可以用“两点确定一条直线”来解释的现象是（ ）
A．①②B．②③C．①④D．③④
7．如果代数式的值是3，则代数式的值是（ ）
A．4B．5C．6D．7
8．如图，点E在的延长线上，下列条件中不能判定的是（ ）
A．B．C．D．
二、填空题
9．若与的和为单项式，则 ．
10．已知，，且，则 ．
11．如图，我国山东号航空母舰行驶在B处同时测得黄岩岛A、中国海军南昌号驱逐舰C的方向分别为北偏西和西南方向，则的度数是 ．

12．如图是一个正方体的展开图，如果正方体相对的面上标记的数值相等，则 ．
13．在锐角内部，画出1条射线，可以画出3个锐角，画出2条不同的射线，可以画出6个锐角；画出3条不同的射线，画10条不同的射线，可以画出 个锐角．
三、解答题
14．计算：．
15．先化简，再求值：，其中，．
16．如图．线段，是线段的中点，是线段的中点．
(1)求线段的长；
(2)在线段上有一点，，求的长．
17．已知，和互为倒数，和互为相反数．
(1)求的值；
(2)求的值．
18．如图，已知射线在的外部，，，平分，平分．求的度数．
19．如图1，是一个棱长为的小正方体所搭几何体从上面看得到的平面图形，正方形中的数字表示在该位置小正方体的个数．
(1)请你在如图2表格中画出它从正面和从左面看得到的平面图形．
(2)求该几何体的表面积为___________．
20．已知代数式，其中“⊕”数字印刷不清．
(1)若数字“⊕”猜测成数字3，请化简整式A；
(2)小红说：代数式A的值只与y有关，根据小红说法，求出“⊕”代表的数字．
21．将一副三角板中的两块直角三角尺的直角顶点按如图所示的方式叠放在一起．
(1)若，则的度数为 ；
(2)若，求的度数；
(3)猜想与之间存在什么数量关系？并说明理由：
22．母亲节，阳阳送给妈妈一份精美的礼物，并用丝带把长方体礼品盒打上包装（如图所示，图中虚线为丝带），打蝴蝶结的部分需用丝带．
(1)用含、、的式子求出打好整个包装需用丝带总长度；
(2)若1米丝带费用为3元，求当，，时，（1）中丝带的总费用为多少元？
23．为积极响应政府提出的“绿色发展低碳出行”号召，某自行车厂决定生产一批共享单车投入市场．该厂原计划一周生产辆共享单车，平均每天生产辆，由于各种原因实际每天生产量与计划量相比有出入．下表是某周的生产情况超产为正、减产为负：
(1)根据记录可知前三天共生产__辆；
(2)产量最多的一天比产量最少的一天多生产__辆；
(3)该厂实行每周计件工资制，每生产一辆车可得元，若超额完成任务，则超过部分每辆另奖元；少生产一辆扣元，那么该厂工人这一周的工资总额是多少？
24．请把下列证明过程补充完整．
已知：如图，B、C、E三点在同一直线上，A、F、E三点在同一直线上，，，求证：．
证明∶ ∵（已知），
∴________（______），
∴____（______），
∵（已知），
∴____（等量代换），
∵（已知），
∴，即，
∴____（等量代换），
∴（_____）．
25．在解决数学问题的过程中，我们常用到“分类讨论”的数学思想，下面是运用分类讨论的数学思想解决问题的过程，请仔细阅读，并解答问题．
【提出问题】三个有理数a，b，c满足，求的值．
【解决问题】解：由题意，得a，b，c三个有理数都为正数或其中一个为正数，另两个为负数．
①a，b，c都是正数，即，，时，则；
②当a，b，c中有一个为正数，另两个为负数时，不妨设，，，则．综上所述，值为3或．
【探究拓展】请根据上面的解题思路解答下面的问题：
(1)已知a，b是不为0的有理数，当时，则的值是________；
(2)已知a，b，c是有理数，当时，求的值；
(3)已知a，b，c是有理数，，，求的值．
26．已知，点为之外任意一点．

（1）如图1，探究与之间的数量关系，并说明理由；
（2）如图2，探究与之间的数量关系，并说明理由．
【拓展变式】如图，“抖空竹”是国家级非物质文化遗产．在“抖空竹”的一个瞬间如图1所示，将图1抽象成一个数学问题：如图2，若，则_______________．

星期
一
二
三
四
五
六
日
增减
参考答案：
1．D
【分析】此题主要考查了有理数大小比较的方法，要熟练掌握，解答此题的关键是要明确：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小．
根据有理数大小比较的法则判定即可．
【详解】解：∵
∴四个数中，最小的数是．
故选：D．
2．C
【分析】此题考查了数轴上的点和数之间的对应关系．与点A相距5个单位长度的点可能在点A的左边，也可能在点A的右边，再根据“左减右加”进行计算．
【详解】解：当要求的点在点A的左边时，则；
当要求的点在点A的右边时，则．
故选：C．
3．D
【分析】本题考查了认识立体图形，熟练掌握每一种几何体的特征是解题的关键．
【详解】解：A． 是四棱锥，故A不符合题意；
B． 是圆柱，故B不符合题意；
C． 是四棱柱，故C不符合题意；
D． 是圆锥，故D符合题意．
故选：D．
4．A
【分析】本题考查了近似数及精确度的问题．根据近似数与精确度的定义对各选项分析判断后求解．
【详解】解：A、精确到千位，故本选项符合题意；
B、近似数精确到十分位，故本选项不符合题意；
C、近似数和近似数精确度不同，则表示的意义不相同，故本选项不符合题意；
D、近似数5万与近似数50000的精确度不相同，故不符合题意；
故选：A．
5．B
【分析】本题考查了图形类规律，根据图形找到前几个图形的规律，进而即可求解．
【详解】解：第1个图案由3个基础图形组成，即，
第2个图案由5个基础图形组成，
第3个图案由7个基础图形组成，
…，
第个图案中的基础图形个数为，
即当时，，
故选：B．
6．C
【分析】本题主要考查了两点确定一条直线，两点之间线段最短，点到直线的距离等等，熟练掌握两点确定一条直线的概念是解题的关键．
【详解】解：①用两根钉子就可以把一根木条固定在墙上，利用了两点确定一条直线，符合题意；
②把弯曲的公路改直，就能够缩短路程，利用“两点之间线段最短”，不符合题意；
③体育课上测量某个同学的跳远成绩，利用了点到直线的距离，不符合题意；
④建筑工人砌墙时，经常先在两端立桩拉线，然后沿着线砌墙，利用了两点确定一条直线，符合题意；
故选C．
7．B
【分析】本题主要考查了代数式求值，先根据题意得到，再由，把整体代入求解即可．
【详解】解：∵代数式的值是3，
∴，
∴，
故选：B．
8．B
【分析】此题主要考查了平行线的判定，根据平行线的判定定理同位角相等，两直线平行．内错角相等，两直线平行．同旁内角互补，两直线平行分别进行分析．关键是掌握平行线的判定定理．
【详解】解：，
，故选项A不合题意；
，
，不能判定，故选项B符合题意；
，
，故选项C不合题意；
∵，
，故选项D不合题意．
故选：B．
9．
【分析】本题考查同类项的定义，合并同类项，代数式求值．注意同类项定义中的两个“相同”：相同字母的指数相同，是易混点．根据“同类项是所含字母相同且相同字母的指数也相同的两个单项式”，可得、的值，再代入求值，即可解答．
【详解】解：与的和为单项式，
与是同类项，
，，
，
故答案为：．
10．5或9
【分析】根据绝对值的定义结合可得或，再计算有理数的减法即可．
【详解】解：因为，，，
所以，，，
因为，
所以或，
当时，；
当时，；
故答案为：5或9．
【点睛】本题考查了有理数的绝对值和减法运算，正确分类、掌握有理数的运算法则是解题的关键．
11．/105度
【分析】根据方向角的定义即可作出判断．
【详解】解：如图，

由题意，得，，
∴．
故答案为：．
【点睛】本题主要考查了方向角的定义，用方向角描述方向时，通常以正北或正南方向为角的始边，以对象所处的射线为终边．
12．0
【分析】本题主要考查了正方体相对两个面上的文字，代数式求值，根据正方体的表面展开图，相对的面之间一定相隔一个正方形，得到、的值是解决问题的关键．
【详解】解：这是一个正方体的平面展开图，共有六个面，
其中面“”与面“1”相对，面“”与面“2”相对，面“”与面“”相对，
根据题意得， ，，
∴．
故答案为：0．
13．66
【分析】考查了角的概念，解决改题的关键是找到规律．分别找出各图形中锐角的个数，找出规律解题．
【详解】解：∵在锐角内部，画出1条射线，可以画出个锐角，
画出2条不同的射线，可以画出个锐角；
画出3条不同的射线，画条不同的射线，
……
∴从一个角的内部引出n条射线所得到的锐角的个数是
，
∴画10条不同射线，可得锐角．
故答案为：66．
14．
【分析】本题考查的是含乘方的有理数的混合运算，先计算乘方，绝对值，再计算除法运算，最后计算加减运算即可，掌握运算顺序是解本题的关键．
【详解】解：
；
15．，
【分析】本题主要考查了整式化简求值，解题的关键是熟练掌握去括号合并同类项法则，注意括号前面为负号时，将括号和负号去掉后，括号内每一项的符号要发生改变．
【详解】解：
，
当，时，原式．
16．(1)15
(2)或12
【分析】本题考查与线段中点有关的计算．
（1）中点平分线段求出的长，再利用，计算即可；
（2）分点在点左侧和右侧两种情况，进行求解即可．
正确的识图，找准线段之间的和差关系，是解题的关键．
【详解】（1）解：∵线段，是线段的中点，
∴，
∵是线段的中点，
∴，
∴；
（2）∵，
∴，
当点在点左侧时：；
当点在点右侧时：．
综上：或12．
17．(1)；
(2)或．
【分析】（）根据绝对值的概念求解即可；
（）将，，分别代入计算即可；
此题考查了有理数的有关概念及运算，代数式求值，解题的关键是正确理解绝对值，相反数和倒数的概念．
【详解】（1）∵，
∴；
（2）∵和互为倒数, 和互为相反数，
∴，，
分类讨论如下：
当时，，
当时，，
∴原式的值为或．
18．
【分析】本题主要考查了角平分线的定义，根据角平分线的定义求出以及的度数是解题的关键．直接利用角平分线的性质结合已知角得出以及的度数，进而得出答案．
【详解】解：因为，，
所以
因为平分，平分，
所以，．
所以．
19．(1)画图见解析
(2)
【分析】本题考查从不同方向看几何体．堆砌图形的表面积，由从上面看小正方形内的数字，可知从正面看的列数与从上面看的列数相同，且每列小正方形数目为从上面看到的该列小正方形数字中的最大数字．从左边看的列数与从上面看的行数相同，且每列小正方形数目为从上面看到的相应行中正方形数字中的最大数字．
（1）由已知条件可知，从正面看有3列，每列小正方形数目分别为3、2、3，从左边看有2列，每列小正方形数目分别为3、3．据此可画出图形即可．
（2）由从三个方向可看到的正方形数量，从而可得表面积．
【详解】（1）解：如图所示：
（2）该几何体的表面积为.
20．(1)
(2)2
【分析】本题主要考查整式的加减运算和解一元一次方程，
将3代入，去括号后按照整式的加减运算即可；
设“⊕”为数字a，将代数式整理后，结合题意可得求解即可．
【详解】（1）解∶当“⊕”猜测成数字3时，
；
（2）设“⊕”为数字a，
则，
∵代数式A的值只与y有关，
∴，
∴．
21．(1)
(2)
(3)，理由见解析
【分析】本题考查了角的和与差，能够根据图形正确表示两个角的和与差是解题关键．
（1）根据和的度数，求得的度数，再根据求得的度数；
（2）根据和的度数，求得的度数，再根据求得的度数；
（3）根据以及，进行计算即可得出结论．
【详解】（1）解：由题意可得：，
∵，
∴，
∵，
∴；
故答案为：；
（2）解：∵，
∴，
∴；
（3）解：猜想：，
理由如下：
∵，
又∵，
∴，
即．
22．(1)打好整个包装需用丝带总长度为（3x＋3y＋3z）cm；
(2)丝带的总费用为4.41元．
【分析】（1）根据把长方体礼品盒打上包装在长方体表面上与宽同长度的丝带有2段，与长同长的丝带也有2段，与高同长的丝带有4段，再加上打结丝带长就是所用丝带的总长度，由整式的加减计算即可；
（2）根据（1）中计算的总长度再乘以丝带的单价即可．
【详解】（1）解：由题意得打好整个包装需用丝带总长度为
2x＋4y＋2z＋（x－y＋z）
＝2x＋4y＋2z＋x－y＋z
＝（3x＋3y＋3z）cm，
答：打好整个包装需用丝带总长度为（3x＋3y＋3z）cm．
（2）解：当，，时，
3x＋3y＋3z
＝3×25＋3×14＋3×10
＝147（cm）
147cm＝1.47米，
所需费用为1.47×3＝4.41元，
答：丝带的总费用为4.41元．
【点睛】此题考查了列代数式、整式的加减及化简求值等知识，熟练掌握整式的加减是解题的关键．
23．(1)599
(2)26
(3)工人这一周的工资总额是元
【分析】（1）本题考查了正数和负数的应用，解答本题的关键在于需要明确“+”是比计划多，“-”是比计划少，根据表格信息将前三天产量相加即可解答本题．
（2）本题考查了有理数以及有理数的加减混合运算，解答本题的关键在于从表格中获得产量最多和最少的信息，再进行相减即可求解．
（3）本题考查了有理数以及有理数的加、减、乘混合运算，工资总额包括生产量乘以60元，再加上超额完成的量乘以15元，两部分相加即可计算工资总额．
【详解】（1）解：根据表格前三天产量为：
（辆）
故答案为：．
（2）一周的产量分别为：，，，，，，，
则产量最多的一天比产量最少的一天多生产：（辆）
故答案为．
（3）超额完成量：
（辆）
总工资：（元）．
答：该厂工人这一周的工资总额是元．
24．；；内错角相等，两直线平行；；两直线平行，内错角相等；；；同位角相等，两直线平行．
【分析】本题主要考查平行线的判定和性质，根据已知利用内错角相等得，则有，等量代换得，结合已知进一步得，利用同位角相等则有．
【详解】证明∶ ∵（已知），
∴（内错角相等，两直线平行），
∴（两直线平行，内错角相等），
∵（已知），
∴（等量代换），
∵（已知），
∴，即，
∴（等量代换），
∴（同位角相等，两直线平行）．
25．(1)0
(2)或1
(3)
【分析】本题考查了绝对值的意义，有理数的加法运算；利用分类讨论的思想解决问题是解题关键．
（1）由题意可知，a、b中一个为正数，一个为负数，根据绝对值的意义化简求值即可；
（2）由题意可知，a，b，c三个有理数都为负数或其中一个为负数，另两个为正数，根据绝对值的意义分别化简求值即可；
（3）由题意可知，a，b，c中一个为负数，另两个为正数，根据绝对值的意义化简求值即可．
【详解】（1）解：当时，a、b中一个为正数，一个为负数，
若，，
则，
若，
则，
故答案为：0；
（2）解：由题意，得a，b，c三个有理数都为负数或其中一个为负数，另两个为正数，
①a，b，c都是负数，即，，时，
则；
②当a，b，c中有一个为负数，另两个为正数时，不妨设，，，
则，
综上所述，值为或；
（3）解：由，可知，a，b，c三个中一个为负数，另两个为正数，
不妨设，，，
则，，，
．
26．（1），理由见解析；（2），理由见解析；[拓展变式]．
【分析】（1）过点作，则，根据平行线的性质可得，进而得出结论；
（2）理由如下：过点作，则，根据平行线的性质可得，，进而得出结论；
（3）过点作，则，根据平行线的性质得出，，进而即可求解．
【详解】解：（1）．理由如下：
过点作，则．

．
，
．
（2）．
理由如下：过点作，则．

，．
，
．
【拓展变式】过点作，则．

，
，
故答案为：．
【点睛】本题考查了平行线的性质与判定，熟练掌握平行线的性质与判定是解题的关键．