2023-2024学年浙江省湖州市吴兴区十校联考数学九上期末质量跟踪监视试题含答案

这是一份2023-2024学年浙江省湖州市吴兴区十校联考数学九上期末质量跟踪监视试题含答案，共7页。试卷主要包含了如图，已知，下列事件中为必然事件的是等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
考生须知：
1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。
一、选择题（每题4分，共48分）
1．已有甲、乙、丙三人，甲说乙在说谎，乙说丙在说谎，丙说甲和乙都在说谎，则（ ）
A．甲说实话，乙和丙说谎B．乙说实话，甲和丙说谎
C．丙说实话，甲和乙说谎D．甲、乙、丙都说谎
2．下列选项的图形是中心对称图形的是（ ）
A．B．C．D．
3．在中， ，则( )．
A．B．C．D．
4．如图：已知，且，则（ ）
A．5B．3C．3. 2D．4
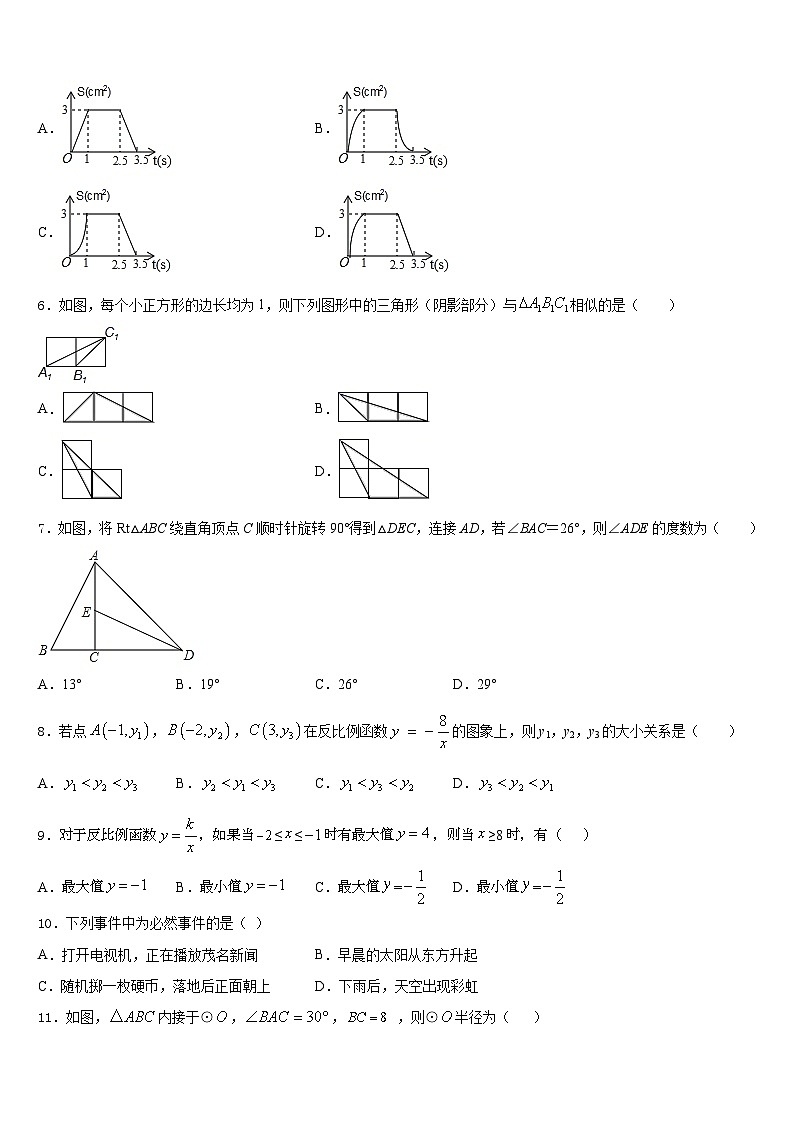
5．已知：如图，矩形ABCD中，AB＝2cm，AD＝3cm．点P和点Q同时从点A出发，点P以3cm/s的速度沿A→D方向运动到点D为止，点Q以2cm/s的速度沿A→B→C→D方向运动到点D为止，则△APQ的面积S（cm2）与运动时间t（s）之间函数关系的大致图象是（ ）
A．B．
C．D．
6．如图，每个小正方形的边长均为1，则下列图形中的三角形（阴影部分）与相似的是（ ）
A．B．
C．D．
7．如图，将Rt△ABC绕直角顶点C顺时针旋转90°得到△DEC，连接AD，若∠BAC＝26°，则∠ADE的度数为（ ）
A．13°B．19°C．26°D．29°
8．若点，，在反比例函数的图象上，则y1，y2，y3的大小关系是（ ）
A．B．C．D．
9．对于反比例函数，如果当≤≤时有最大值，则当≥8时，有（ ）
A．最大值B．最小值C．最大值=D．最小值=
10．下列事件中为必然事件的是（ ）
A．打开电视机，正在播放茂名新闻B．早晨的太阳从东方升起
C．随机掷一枚硬币，落地后正面朝上D．下雨后，天空出现彩虹
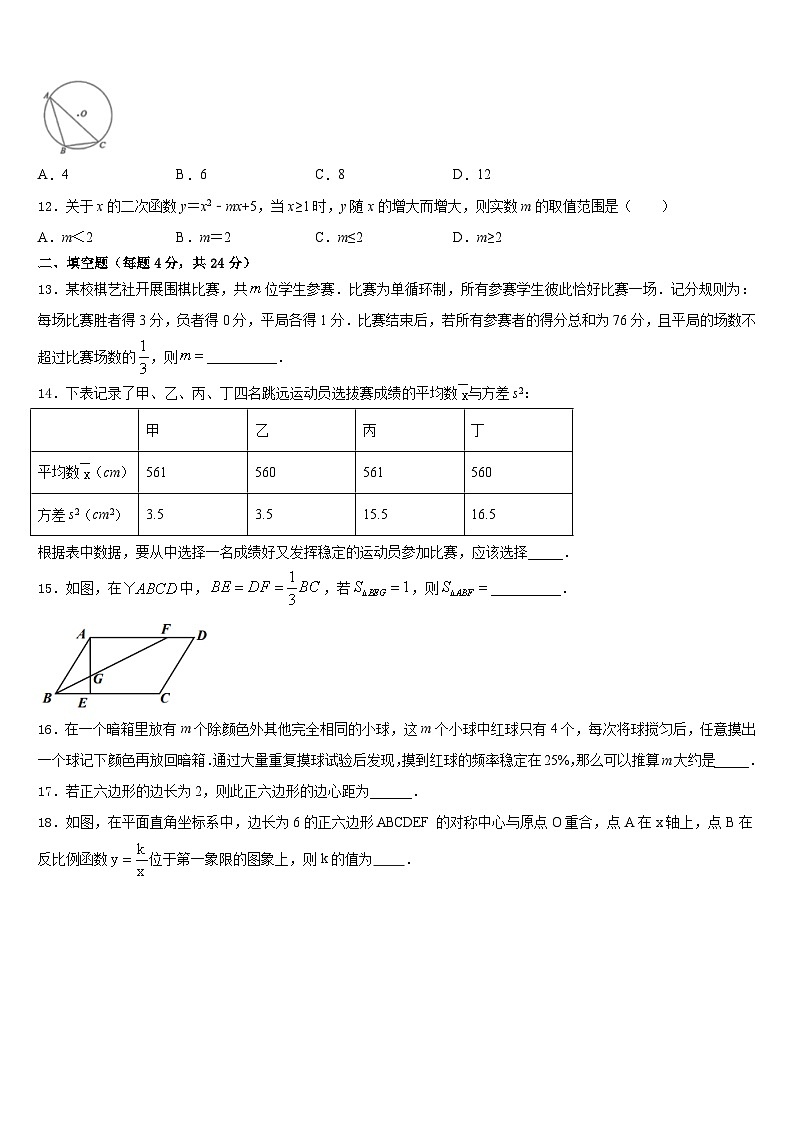
11．如图，内接于⊙，， ，则⊙半径为（ ）
A．4B．6C．8D．12
12．关于x的二次函数y＝x2﹣mx+5，当x≥1时，y随x的增大而增大，则实数m的取值范围是（ ）
A．m＜2B．m＝2C．m≤2D．m≥2
二、填空题（每题4分，共24分）
13．某校棋艺社开展围棋比赛，共位学生参赛．比赛为单循环制，所有参赛学生彼此恰好比赛一场．记分规则为：每场比赛胜者得3分，负者得0分，平局各得1分．比赛结束后，若所有参赛者的得分总和为76分，且平局的场数不超过比赛场数的，则__________．
14．下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差s2：
根据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择_____．
15．如图，在中，，若，则__________．
16．在一个暗箱里放有m个除颜色外其他完全相同的小球，这m个小球中红球只有4个，每次将球搅匀后，任意摸出一个球记下颜色再放回暗箱．通过大量重复摸球试验后发现，摸到红球的频率稳定在25%，那么可以推算m大约是_____．
17．若正六边形的边长为2，则此正六边形的边心距为______．
18．如图，在平面直角坐标系中，边长为6的正六边形ABCDEF的对称中心与原点O重合，点A在x轴上，点B在反比例函数位于第一象限的图象上，则k的值为 ．
三、解答题（共78分）
19．（8分）已知：如图，在菱形ABCD中，E为BC边上一点，∠AED=∠B．
（1）求证：△ABE∽△DEA；
（2）若AB=4，求AE•DE的值．
20．（8分）如图，⊙O的直径AB为10cm，弦BC为6cm，D，E分别是∠ACB的平分线与⊙O，直径AB的交点，P为AB延长线上一点，且PC＝PE．
（1）求AC、AD的长；
（2）试判断直线PC与⊙O的位置关系，并说明理由．
21．（8分）计算：
（1）sin30°-（5- tan75°）0 ； （2） 3 tan230°-sin45°＋sin60°．
22．（10分）光明中学以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨举办首届《诗词大会》，九年级2班的马小梅晋级总决赛，比赛过程分两个环节，参赛选手须在每个环节中各选择一道题目.
第一环节：横扫千军、你说我猜、初级飞花令，（分别用）表示；
第二环节：出口成诗、飞花令、超级飞花令、诗词接龙（分别用表示）.
（1）请用画树状图或列表的方法表示马小梅参加总决赛抽取题目的所有可能结果；
（2）求马小梅参加总决赛抽取题目都是飞花令题目（初级飞花令、飞花令、超级飞花令）的概率.
23．（10分）一个不透明袋子中装有2个白球，3个黄球，除颜色外其它完全相同．将球摇匀后，从中摸出一个球不放回，再随机摸出一球，两次摸到的球颜色相同的概率是______．
24．（10分）如图，已知⊙O的直径AC与弦BD相交于点F，点E是DB延长线上的一点，∠EAB=∠ADB．
（1）求证：AE是⊙O的切线；
（2）已知点B是EF的中点，求证：△EAF∽△CBA；
（3）已知AF=4，CF=2，在（2）的条件下，求AE的长．
25．（12分）如图，抛物线y=ax2+bx+c (a≠0)过点M(-2，3)，顶点坐标为N(-1，4)，且与x轴交于A、B两点，与y轴交于C点．
（1）求抛物线的解析式；
（2）点P为抛物线对称轴上的动点，当PM+PB的值最小时，求点P的坐标；
26．（12分）如图，直线与轴交于点，与轴交于点，抛物线与直线交于，两点，点是抛物线的顶点．

（1）求抛物线的解析式；
（2）点是直线上方抛物线上的一个动点，其横坐标为，过点作轴的垂线，交直线于点，当线段的长度最大时，求的值及的最大值．
（3）在抛物线上是否存在异于、的点，使中边上的高为，若存在求出点的坐标；若不存在请说明理由．
参考答案
一、选择题（每题4分，共48分）
1、B
2、B
3、A
4、C
5、C
6、B
7、B
8、D
9、D
10、B
11、C
12、C
二、填空题（每题4分，共24分）
13、1
14、甲
15、6
16、1
17、.
18、
三、解答题（共78分）
19、（1）见解析；（2）2
20、（1）AC＝8cm；AD＝cm；（2）PC与圆⊙O相切，理由见解析
21、（1）﹣（2）
22、（1）详见解析；（2）
23、
24、（1）证明见解析；（2）证明见解析；（3）．
25、（1）二次函数的解析式为：；（2）点P的坐标为(-1，2)
26、（1）；（2）当时，PM有最大值；（3）存在，理由见解析；，，，
甲
乙
丙
丁
平均数（cm）
561
560
561
560
方差s2（cm2）
3.5
3.5
15.5
16.5