2023-2024学年山东省泰安市新泰市数学九年级第一学期期末统考模拟试题含答案

这是一份2023-2024学年山东省泰安市新泰市数学九年级第一学期期末统考模拟试题含答案，共8页。

学校_______ 年级_______ 姓名_______
考生须知：
1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。
一、选择题（每题4分，共48分）
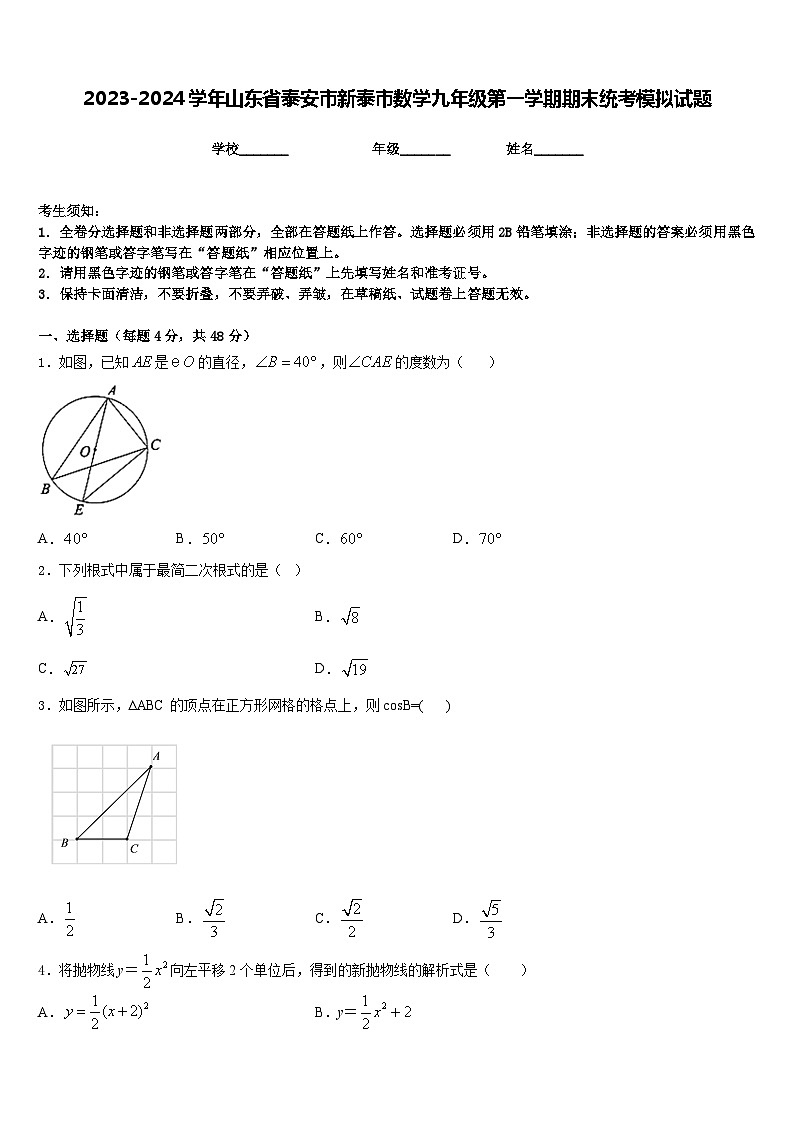
1．如图，已知是的直径，，则的度数为（ ）
A．B．C．D．
2．下列根式中属于最简二次根式的是（ ）
A．B．
C．D．
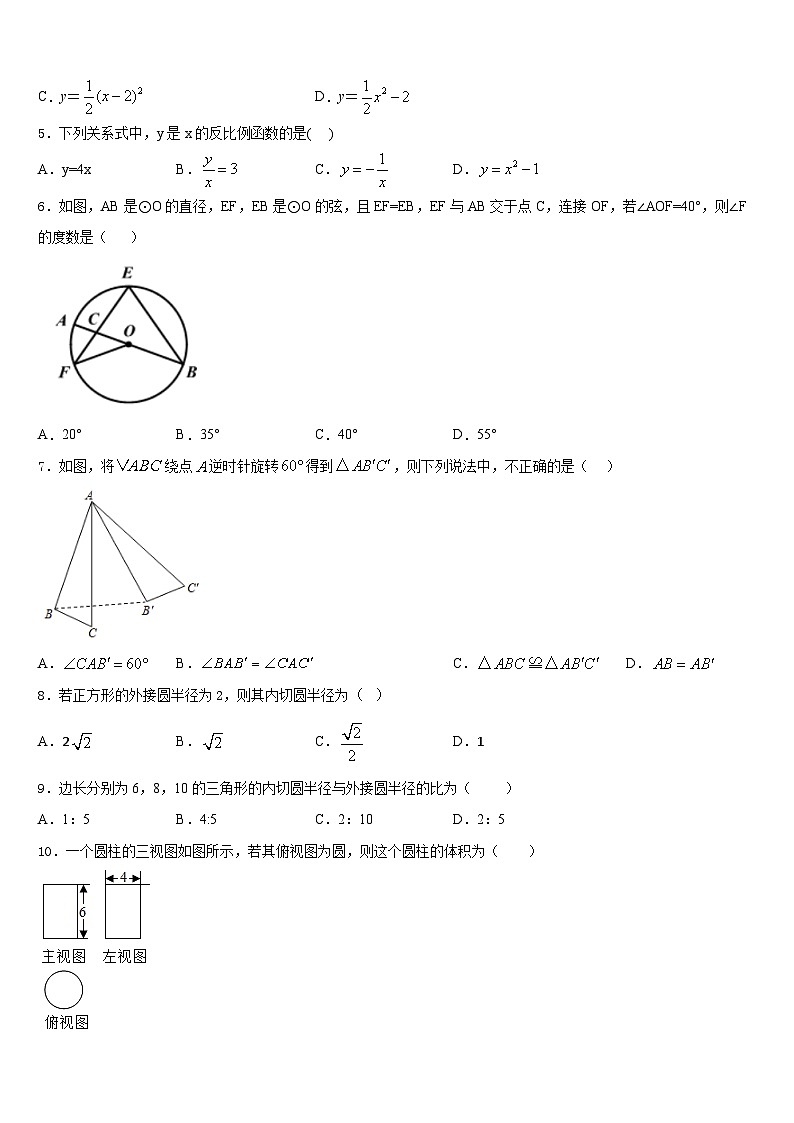
3．如图所示，∆ABC的顶点在正方形网格的格点上，则csB=( )
A．B．C．D．
4．将抛物线y＝向左平移2个单位后，得到的新抛物线的解析式是（ ）
A．B．y＝
C．y＝D．y＝
5．下列关系式中，y是x的反比例函数的是( )
A．y=4xB．C．D．
6．如图，AB是⊙O的直径，EF，EB是⊙O的弦，且EF=EB，EF与AB交于点C，连接OF，若∠AOF=40°，则∠F的度数是（ ）
A．20°B．35°C．40°D．55°
7．如图，将绕点逆时针旋转得到，则下列说法中，不正确的是（ ）
A．B．C．D．
8．若正方形的外接圆半径为2，则其内切圆半径为（ ）
A．2B．C．D．1
9．边长分别为6，8，10的三角形的内切圆半径与外接圆半径的比为（ ）
A．1：5B．4:5C．2：10D．2：5
10．一个圆柱的三视图如图所示，若其俯视图为圆，则这个圆柱的体积为（ ）
A．B．C．D．
11．抛物线y＝3（x+2）2﹣（m2+1）（m为常数）的顶点在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
12．已知点A（1，a）、点B（b，2）关于原点对称，则a+b的值为（ ）
A．3B．-3C．-1D．1
二、填空题（每题4分，共24分）
13．如图，点C是以AB为直径的半圆上一个动点（不与点A、B重合），且AC+BC=8，若AB=m（m为整数），则整数m的值为______．
14．如图，在Rt△ABC中，∠ACB=90º ，将△ABC绕顶点C逆时针旋转得到△A′B′C，M是BC的中点，N是A′B′的中点，连接MN，若BC=2 cm,∠ABC=60°，则线段MN的最大值为_____.
15．已知线段c是线段、的比例中项，且，，则线段c的长度为______．
16．如图，在Rt△ABC中，∠ACB＝90°，∠ABC＝30°，将△ABC绕点C顺时针旋转至△A′B′C，使得点A′恰好落在AB上，则旋转角度为_____．
17．已知扇形的圆心角为120°，弧长为6π，则它的半径为________．
18．如图，矩形ABOC的顶点B、C分别在x轴、y轴上，顶点A在第一象限，点B的坐标为（，0），将线段OC绕点O顺时针旋转60°至线段OD，若反比例函数 （k≠0）的图象进过A、D两点，则k值为_____．
三、解答题（共78分）
19．（8分）问题情境:在综合实践课上，老师让同学们以“菱形纸片的剪拼”为主题开展数学活动，如图（1），将一张菱形纸片ABCD（∠BAD＝60°）沿对角线AC剪开，得到△ABC和△ACD
操作发现:（1）将图（1）中的△ABC以A为旋转中心，顺时针方向旋转角α（0°＜α＜60°）得到如图（2）所示△ABC′，分别延长BC′和DC交于点E，发现CE＝C′E．请你证明这个结论．
（2）在问题（1）的基础上，当旋转角α等于多少度时，四边形ACEC′是菱形？请你利用图（3）说明理由．
拓展探究:（3）在满足问题（2）的基础上，过点C′作C′F⊥AC，与DC交于点F．试判断AD、DF与AC的数量关系，并说明理由．
20．（8分）如图，若是由ABC平移后得到的，且中任意一点经过平移后的对应点为
(1)求点小的坐标．
(2)求的面积．
21．（8分）如图，某城建部门计划在新修的城市广场的一块长方形空地上修建一个面积为1200m2的停车场，将停车场四周余下的空地修建成同样宽的通道，已知长方形空地的长为50m，宽为40m．
（1）求通道的宽度；
（2）某公司希望用80万元的承包金额承揽修建广场的工程，城建部门认为金额太高需要降价，通过两次协商，最终以51.2万元达成一致，若两次降价的百分率相同，求每次降价的百分率．
22．（10分）现有甲、乙、丙三人组成的篮球训练小组，他们三人之间进行互相传球练习，篮球从一个人手中随机传到另外一个人手中计作传球一次，共连续传球三次．
（1）若开始时篮球在甲手中，则经过第一次传球后，篮球落在丙的手中的概率是 ；
（2）若开始时篮球在甲手中，求经过连续三次传球后，篮球传到乙的手中的概率．（请用画树状图或列表等方法求解）
23．（10分）如图，正方形ABCD，将边BC绕点B逆时针旋转60°，得到线段BE，连接AE，CE．
（1）求∠BAE的度数；
（2）连结BD，延长AE交BD于点F．
①求证：DF=EF；
②直接用等式表示线段AB，CF，EF的数量关系．
24．（10分）已知：正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB，DC、DC（或它们的延长线）于点M，N.
（1）当∠MAN绕点A旋转到（如图1）时，求证：BM+DN=MN；
（2）当∠MAN绕点A旋转到如图2的位置时，猜想线段BM，DN和MN之间又有怎样的数量关系呢？请直接写出你的猜想。（不需要证明）
25．（12分）为了解决农民工子女就近入学问题，我市第一小学计划2012年秋季学期扩大办学规模．学校决定开支八万元全部用于购买课桌凳、办公桌椅和电脑，要求购买的课桌凳与办公桌椅的数量比为20:1，购买电脑的资金不低于16000元，但不超过24000元．已知一套办公桌椅比一套课桌凳贵80元，用2000元恰好可以买到10套课桌凳和4套办公桌椅．（课桌凳和办公桌椅均成套购进）
（1）一套课桌凳和一套办公桌椅的价格分别为多少元？
（2）求出课桌凳和办公桌椅的购买方案．
26．（12分）某商场“六一”期间进行一个有奖销售的活动,设立了一个可以自由转动的转盘(如图),并规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
(1)计算并完成上述表格;
(2)请估计当n很大时,频率将会接近__________;假如你去转动该转盘一次,你获得“可乐”的概率约是__________;(结果精确到0.1)
(3)在该转盘中,表示“车模”区域的扇形的圆心角约是多少度?
参考答案
一、选择题（每题4分，共48分）
1、B
2、D
3、C
4、A
5、C
6、B
7、A
8、B
9、D
10、B
11、C
12、B
二、填空题（每题4分，共24分）
13、6或1
14、3 cm
15、6
16、60°
17、1
18、4
三、解答题（共78分）
19、（1）见解析；（2）当α＝30°时，四边形AC′EC是菱形，理由见解析；（3）AD+DF＝AC，理由见解析
20、（1）（-1，5），（-2，3），（-4，4）；（2）三角形面积为2.5；
21、（1）5m，（2）20%
22、（1）经过第一次传球后，篮球落在丙的手中的概率为；（2）篮球传到乙的手中的概率为．
23、 (1) 75°;(2)①见解析②
24、（1）见解析；（2）DN-BM=MN
25、（1）分别为120元、200元（2）有三种购买方案，见解析
26、（1）472，0.596；（2）0.6，0.6；（3）144°.
转动转盘的次数n
100
200
400
500
800
1 000
落在“可乐”区域
的次数m
60
122
240
298
604
落在“可乐”
区域的频率
0.6
0.61
0.6
0.59
0.604