福建省三明市永安市2020-2021学年八年级上学期数学期末考试试卷

这是一份福建省三明市永安市2020-2021学年八年级上学期数学期末考试试卷，共17页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题（共10小题，每小题4分，满分40分）
1．△ABC 中， ∠A 、 ∠B 、 ∠C 的对边分别为a、b、c，若 a2=b2+c2 ，则有（ ）
A．∠A=90°B．∠B=90°C．∠C=90°D．∠C=∠A+∠B
2．下列说法中正确的是（ ）．
A．0.09的平方根是0.3B．16=±4
C．0的立方根是0D．1的立方根是 ±1
3．已知点M（3，﹣2），N（3，﹣1），则线段MN与x轴（ ）
A．垂直B．平行C．相交D．不垂直
4．若 m<27A．3B．4C．5D．6
5．下列运算，结果正确的是（ ）
A．5−3=2B．3+2=32C．6÷2=3D．6×2=23
6．在一次青年歌手比赛中，七位评委为某位歌手打出的分数如下：9.5，9.4，9.6，9.9，9.3，9.7，9.0（单位：分）．若去掉一个最高分和一个最低分，则去掉前与去掉后没有改变的一个统计量是（ ）
A．平均分B．方差C．中位数D．极差
7．《九章算术》是中国古代第一部数学专著，它对我国古代后世的数学家产生了深远的影响，该书中记载了一个问题，大意是：有几个人一起去买一件物品，每人出8元，多3元；每人出7元，少4元，问有多少人？该物品价几何？设有x人，物品价值y元，则所列方程组正确的是（ ）
A．8y+3=x7y−4=xB．8x+3=y7x−4=y
C．8x−3=y7x+4=yD．8y−3=x7y+4=x
8．如图，直线 a⊥b ，在某平面直角坐标系中，x轴 //a ，y轴 //b ，点A的坐标为 (−3,2) ，点B的坐标为 (2,−3) ，则坐标原点为（ ）
A．O1B．O2C．O3D．O4
9．一组数据2，0，1，4，3，这组数据的方差是（ ）
A．2B．4C．1D．3
10．当k取不同的值时，y关于x的函数y=kx+2（k≠0）的图象为总是经过点（0，2）的直线，我们把所有这样的直线合起来，称为经过点（0，2）的“直线束”.那么，下面经过点（﹣1，2）的直线束的函数式是（ ）
A．y=kx﹣2（k≠0）B．y=kx+k+2（k≠0）
C．y=kx﹣k+2（k≠0）D．y=kx+k﹣2（k≠0）
二、填空题（共6小题，每小题4分，满分24分）
11．计算： 3−8 = ．
12．把命题“对顶角相等”改写成“如果…那么…”的形式是 .
13．将一个含 45∘ 的三角尺和一把直尺按如图所示摆放，若 ∠1=20° ，则 ∠2= ∘ ．
14．在如图的方格中，若要使横，竖，斜对角的3个实数相乘都得到同样的结果，则图中m的值为 .
15．已知一次函数 y=2x−1 的图象经过 A(x1，1) ， B(x2，3) 两点，则 x1 x2 （填“ > ”“ < ”或“ = ”）.
16．如图1，点P从△ABC的顶点B出发，沿B→C→A匀速运动到点A，图2是点P运动时，线段BP的长度y随时间x变化的关系图象，其中M为曲线部分的最低点，则△ABC的面积是 ．
三、解答题（共9题，满分86分）
17．计算∶
（1）17−28
（2）(1−3)2−|3−2|
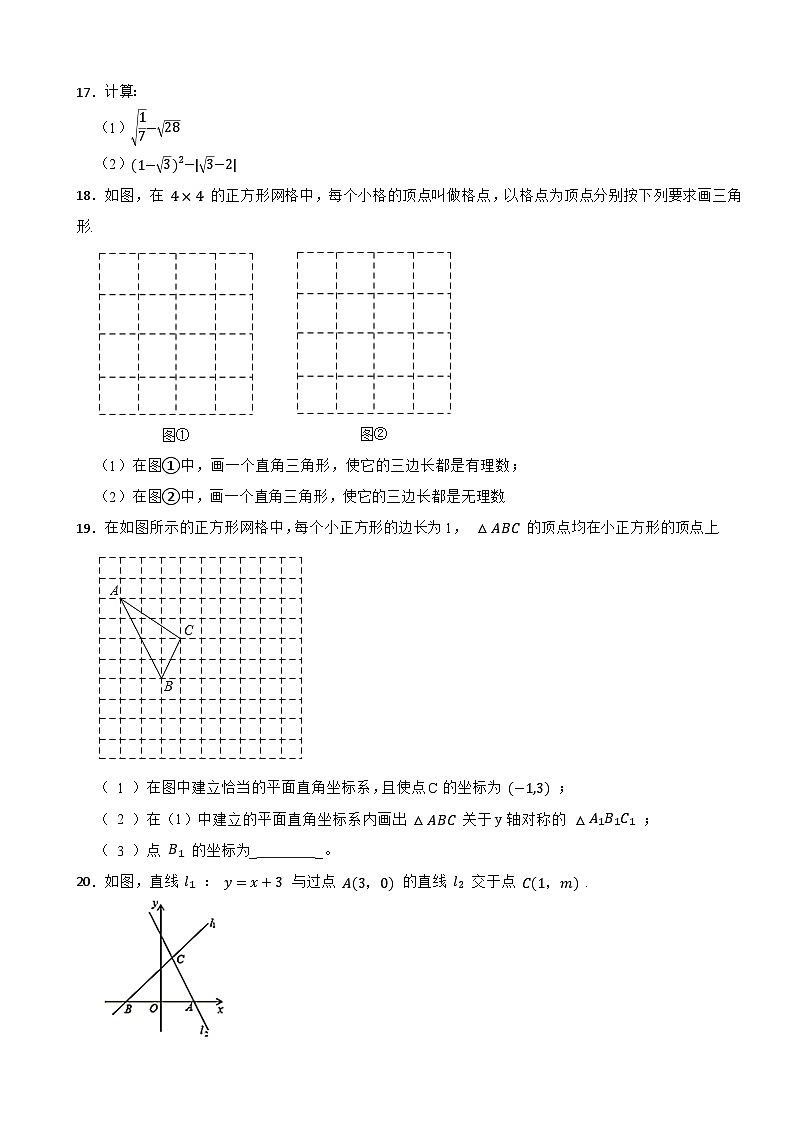
18．如图，在 4×4 的正方形网格中，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形.
（1）在图①中，画一个直角三角形，使它的三边长都是有理数；
（2）在图②中，画一个直角三角形，使它的三边长都是无理数.
19．在如图所示的正方形网格中，每个小正方形的边长为1， △ABC 的顶点均在小正方形的顶点上.
（ 1 ）在图中建立恰当的平面直角坐标系，且使点C的坐标为 (−1,3) ；
（ 2 ）在（1）中建立的平面直角坐标系内画出 △ABC 关于y轴对称的 △A1B1C1 ；
（ 3 ）点 B1 的坐标为_ _。
20．如图，直线 l1 ： y=x+3 与过点 A(3，0) 的直线 l2 交于点 C(1，m) .
（1）求m的值；
（2）求直线 l2 的解析式.
21．某天，一蔬菜经营户从蔬菜批发市场批发了黄瓜和茄子共120千克，到菜市场去卖，黄瓜和茄子当天的批发价和零售价如下表所示∶
（1）若他当天批发两种蔬菜共花去280元，则购进黄瓜和茄子各多少千克？
（2）他当天卖完这些黄瓜和茄子可赚多少元？
22．小江带领村民利用微商平台，在线推广和销售本地特产柑桔.通过一个月的努力跟进，柑桔的销售有了很大的起色，为了了解这个月每户村民的柑桔销售情况，小江随机从A、B两村各抽取20户村民的“柑桔”销量 x （单位∶箱）进行调查，并得到如下统计图表∶
B村柑桔销量统计表
小江在统计中发现，销量低于50箱的具体情况如下∶
A村∶33，40，27，34，49，42，16，48，42，43，48，38
B村∶9，22，40，43，35，48，45，47，30，33，39，30，45
根据上述信息回答下列问题∶
（1）填空∶ a= ， b= .
（2）根据调查数据完成了表中的统计量∶则 m= .
（3）你认为A、B两村中哪个村的柑桔卖得更好？请说明理由.
23．如图，已知∠1+∠2＝180°，∠3＝B，
（1）证明：EF∥AB.
（2）试判断∠AED与∠C的大小关系，并说明你的理由.
24．有些关于方程组的问题，欲求的结果不是每一个未知数的值，而是关于未知数的代数式的值，如以下问题∶
已知实数x、y满足 3x−y=5①， 2x+3y=7②，求 x−4y 和 7x+5y 的值.
本题常规思路是将①②两式联立组成方程组，解得x、y的值再代入欲求值的代数式得到答案，常规思路运算量比较大.其实，仔细观察两个方程未知数的系数之间的关系，本题还可以通过适当变形整体求得代数式的值，如由①−②可得 x−4y=−2 ，由①＋②×2 可得 7x+5y=19 .这样的解题思想就是通常所说的“整体思想”.解决问题∶
（1）已知二元一次方程组 3x+2y=72x+3y=3 则 x−y= ， x+y= .
（2）某班级组织活动购买小奖品，买13支铅笔、5块橡皮、2本日记本共需31元，买25支铅笔、9块橡皮、3本日记本共需55元，则购买3支铅笔、3块橡皮、3本日记本共需多少元？
（3）对于实数x、y，定义新运算∶ x∗y=ax+b+c ，其中a、b、c是常数，等式右边是通常的加法和乘法运算.已知 3∗5=16 ， 2∗3=12 ，那么 5∗9= .
25．已知，在 △ABC 中，点E在边 AB 上，点D是 BC 上一个动点，将 ∠B 沿E、D所在直线进行翻折得到 ∠EFD ，
（1）如图1，若 ∠B=50° ，则 ∠AEF+∠FDC= ；
（2）在图1中细心的小明发现了 ∠AEF ， ∠FDC ， ∠B 之间的关系，请您替小明写出这个数量关系并证明；
（3）小明进一步探索发现∶当 BD= _ _时，有 EF//BD ，请你证明这个结论；
（4）若点D在线段 BC 上运动，问小明发现的 ∠AEF ， ∠FDC ， ∠B 的数量关系会变吗？请你在备用图中画出一个不同于图1的示意图，并直接写出你的结论.
答案解析部分
1．【答案】A
【知识点】勾股定理的逆定理
【解析】【解答】解： ∵a2=b2+c2 ，
∴△ABC 是直角三角形，且 ∠A=90° ，
故答案为：A.
【分析】如果三角形三边长a、b、c满足 a2=b2+c2 ，那么这个三角形是直角三角形，且边a所对的角是直角.
2．【答案】C
【知识点】平方根；算术平方根；立方根及开立方
【解析】【解答】解：A、0.09的平方根是±0.3，不符合题意；
B、 16=4 ，不符合题意；
C、0的立方根是0，符合题意；
D、1的立方根是1，不符合题意；
故答案为：C.
【分析】根据平方根，算术平方根和立方根的定义分别判断即可.
3．【答案】A
【知识点】点的坐标；坐标与图形性质
【解析】【解答】解：∵M（3，﹣2），N（3，﹣1），∴横坐标相同，∴MN⊥x轴，
故答案为：A．
【分析】根据平面直角坐标系中点的坐标特点，当点的横坐标相同时，线段与y轴平行，与x轴垂直即可解答.
4．【答案】C
【知识点】无理数的估值
【解析】【解答】解： 27=28 ，
∵25<28<36 ，
∴5<27<6 ，
又∵m<27∴m=5，
故答案为：C.
【分析】利用27介于5和6之间求解.
5．【答案】D
【知识点】二次根式的乘除法；二次根式的加减法
【解析】【解答】解：A. 5 与 3 不是同类二次根式，不能合并，此选项错误；
B.3与 2 不是同类二次根式，不能合并，此选项错误；
C. 6÷2=6÷2=3 ，此选项错误；
D. 6×2=3×2×2=23 ，此选项计算正确.
故答案为：D.
【分析】（1）由同类二次根式的定义可知5与3不是同类二次根式，所以不能合并；
（2）同理可知不能合并；
（3）由二次根式的除法法则可得原式=3；
（4）由二次根式的乘法法则可得原式=6×2=23.
6．【答案】C
【知识点】中位数
【解析】【解答】将该歌手的分数按从小到大进行排序为9.0，9.3，9.4，9.5，9.6，9.7，9.9
则去掉前其中位数为9.5分
去掉一个最高分和一个最低分，该歌手的分数为9.3，9.4，9.5，9.6，9.7
则去掉后其中位数为9.5分
因此，去掉前与去掉后没有改变的一个统计量是中位数
故答案为：C．
【分析】根据中位数的定义即可得．
7．【答案】C
【知识点】二元一次方程组的应用-古代数学问题
【解析】【解答】根据题意相等关系：①8×人数-3=物品价值，②7×人数+4=物品价值，可列方程组： 8x−3=y7x+4=y ，
故答案为：C.
【分析】 设有x人，物品价值y元 ，根据每人出8元的钱数比物价多出3元及每人出7元的钱数比物价少出4元，列出方程组。
8．【答案】C
【知识点】坐标与图形性质；一次函数的图象
【解析】【解答】解：设过A、B的直线解析式为y=kx+b，
∵点A的坐标为（-3，2），点B的坐标为（2，-3），
∴2=−3k+b−3=2k+b ，
解得 k=−1b=−1 ，
∴直线AB为 y=−x−1 ，
∴直线AB经过第二、三、四象限，
如图，由A、B的坐标可知，沿CD方向为x轴正方向，沿CE方向为y轴正方向，
故将点A沿着CD方向平移3个单位，再沿着EC方向平移2个单位，即可到达原点位置，将点B沿着CE方向平移3个单位，再沿着DC方向平移2个单位，即可到达原点位置，
则原点为点O3.
故答案为：C.
【分析】利用点A的坐标为 (−3,2) ，点B的坐标为 (2,−3) ， 求出直线AB为 y=−x−1 ，经过第二、三、四象限，再估计坐标轴和原点位置即可.
9．【答案】A
【知识点】方差
【解析】【解答】解：∵平均数= 15 ×（2+0+1+4+3）=2，
s2= 15 ×[（2-2）2+（0-2）2+（1-2）2+（4-2）2+（3-2）2]=2.
故选：A．
【分析】先求出这组数据的平均数，然后代入公式求出方差即可．
10．【答案】B
【知识点】一次函数的图象
【解析】【解答】解：在y=kx﹣2中，当x=﹣1时，y=﹣k﹣2≠2，故A选项不合题意；
在y=kx+k+2中，当x=﹣1时，y=﹣k+k+2=2，故B选项符合题意；
在y=kx﹣k+2中，当x=﹣1时，y=﹣k﹣k﹣2=﹣2k﹣2≠2，故C选项不合题意；
在y=kx+k﹣2中，当x=﹣1时，y=﹣k+k﹣2=﹣2≠2，故D选项不合题意.
故答案为：B.
【分析】把x=-1分别代入每一个函数解析式，算出对应的函数值，将该函数值与2进行比较即可得出答案.
11．【答案】﹣2
【知识点】立方根及开立方
【解析】【解答】解： 3−8 =﹣2，
故答案为：﹣2．
【分析】根据立方根的定义，一个数的立方等于-8，则这个数就是-8的立方根。
12．【答案】如果两个角是对顶角，那么这两个角相等
【知识点】定义、命题及定理的概念
【解析】【解答】解：题设为：两个角是对顶角，结论为：这两个角相等，
故写成“如果…那么…”的形式是：如果两个角是对顶角，那么这两个角相等，
故答案为：如果两个角是对顶角，那么这两个角相等．
【分析】命题中的条件是两个角是对顶角，放在“如果”的后面，结论是这两个角相等，应放在“那么”的后面．
13．【答案】25
【知识点】平行线的性质
【解析】【解答】解：如图，
∵AB∥CD，
∴∠3=∠1=20°，
∵三角形是一个含 45∘ 的三角尺，
∴∠2=45°-∠3=25°，
故答案为：25．
【分析】利用平行线的性质可求出∠3的度数；再根据∠2=45°-∠3，可求出∠2的度数.
14．【答案】6
【知识点】一元一次方程的其他应用
【解析】【解答】解：由题意得 1×m×6=3×6×2，
解得： m=6 .
故答案为： 6.
【分析】根据横，竖，斜对角的3个实数相乘都得到同样的结果可以令第二行三个数的积 等于第三列的三个数的积，据此列出方程，求解即可.
15．【答案】<
【知识点】一次函数的性质
【解析】【解答】解：当y=1时， 2x1−1=1 ，
解得： x1=1 ；
当y=3时， 2x2−1=3 ，
解得： x2=2 .
又∵1<2 ，
∴x1故答案为： < .
【分析】将两个点的纵坐标分别代入函数解析式，算出对应的自变量的值，即可比较得出答案.
16．【答案】12
【知识点】函数的图象
【解析】【解答】解：根据图象可知点P在BC上运动时，此时BP不断增大，
由图象可知：点P从B向A运动时，BP的最大值为5，
即BC=5，
由于M是曲线部分的最低点，
∴此时BP最小，
即BP⊥AC，BP=4，
∴由勾股定理可知：PC=3，
由于图象的曲线部分是轴对称图形，
∴PA=3，
∴AC=6，
∴△ABC的面积为： 12 ×4×6=12
故答案为：12
【分析】根据图象可知点P在BC上运动时，此时BP不断增大，而从C向A运动时，BP先变小后变大，从而可求出BC与AC的长度．
17．【答案】（1）解： 17−28
=77−27
=−1377 ；
（2）解： (1−3)2−|3−2|
=1−23+3−(2−3)
=4−23−2+3
=2−3 .
【知识点】实数的运算；二次根式的加减法
【解析】【分析】（1）根据二次根式的性质分别化简，再合并同类二次根式即可；
（2）第一项利用完全平方公式去括号，第二项利用绝对值的意义化简，进而再合并同类项即可.
18．【答案】（1）解：如图①中，△ABC即为所求；
（2）解：如图②中，△ABC即为所求.
【知识点】勾股定理；勾股定理的逆定理
【解析】【分析】（1）利用勾股数3，4，5画图即可；
（2）利用方格纸的特点结合勾股定理得出AB=22，AC=2，BC=10，这时三边满足勾股定理的逆定理且都是无理数.
19．【答案】解：（1）平面直角坐标系如图所示；（2）如图：△A1B1C1为所画图形；（3）如图， B1(2，1) ,
【知识点】点的坐标；作图﹣轴对称
【解析】【分析】（1）将点C向右平移一个单位，再向下平移3个单位后的对应点作为坐标原点，建立平面直角坐标系；
（2）利用网格纸的特点及轴对称的性质，分别作出点A、B、C关于y轴的对称点A1、B1、C1再顺次连接即可；
（3）直接根据点的位置得出其坐标.
20．【答案】（1）解：∵点C（1，m）在一次函数y=x+3的图象上，
∴m=1+3=4；
（2）解：设一次函数图象 l2相应的函数表达式为y=kx+b，
把点A（3，0），C（1，4）代入得
3k+b=0k+b=4 ，
解得 k=−2b=6
∴直线 l2 的解析式为 y=−2x+6 .
【知识点】一次函数的图象；待定系数法求一次函数解析式
【解析】【分析】（1）点在直线上，点的坐标满足表达式，把 C（1，m）代入y=x+3即可得出答案；
（2）用待定系数法求表达式.
21．【答案】（1）解：设购进黄瓜x千克，茄子y千克，
根据题意得： x+y=1202.4x+2.2y=280 ，
解得： x=80y=40 ，
答：购进黄瓜80千克，茄子40千克；
（2）解： 80×(3.6−2.4)+40×(3−2.2)=128 ，
答：卖完这些黄瓜和茄子可赚128元.
【知识点】二元一次方程组的实际应用-销售问题
【解析】【分析】（1） 设购进黄瓜x千克，茄子y千克，利用等量关系“ 黄瓜质量+茄子质量=120 ”“黄瓜钱数+茄子钱数=280 ”，列方程组求解；
（2）由利润=质量×（ 零售价-批发价 ）即可算出答案.
22．【答案】（1）7；2
（2）48
（3）解：我认为A村的柑桔卖得更好，因为A村平均数，中位数与众数都比B村好.
【知识点】统计表；扇形统计图；中位数；分析数据的集中趋势
【解析】【解答】解：（1）由题意得B村销量低于50箱的共13户，
∴a=13-6=7，b=20-13-5=2，
故答案为：7，2；
（2）A村共抽取了20组数据，故中位数m为排序后第10、11个数据的平均数，将A村低于50箱的数据排序为：16，27，33，34，38，40， 42，42，43，48，48，49，
∴m= 48+482=48 ，
故答案为：48；
【分析】(1) B村销量低于50箱的共13户，利用40≤x＜50的6人，求出a=7，再用20减去销量低于60箱的数量即可算出b的值；
(2)将一组数据按照由小到大（或由大到小）的顺序排列，如果数据的个数是奇数，则称处于中间位置的数为这组数据的中位数；如果数据的个数是偶数，则称中间两个数据的平均数为这组数据的中位数，据此即可得出m的值；
(3) 利用平均数，中位数与众数综合评价即可.
23．【答案】（1）证明：∵∠1+∠DFE＝180°（平角定义），∠1+∠2＝180°（已知），
∴∠2＝∠DFE，
∴EF∥AB（内错角相等，两直线平行）；
（2）解：∠AED与∠C相等.
∵EF∥AB，
∴∠3＝∠ADE（两直线平行，内错角相等），
∵∠3＝∠B（已知），
∴∠B＝∠ADE（等量代换），
∴DE∥BC（同位角相等，两直线平行），
∴∠AED＝∠C（两直线平行，同位角相等）.
【知识点】平行线的判定与性质
【解析】【分析】（1）根据同角的补角相等，可得∠2＝∠DFE，根据内错角相等，两直线平行即证结论；
（2）∠AED与∠C相等. 理由： 根据两直线平行，内错角相等，可得∠3＝∠ADE，由等量代换，可得∠B＝∠ADE，根据同位角相等，两直线平行，可得DE∥BC，根据两直线平行，同位角相等，可得∠AED＝∠C.
24．【答案】（1）4；2
（2）解：设购买1支铅笔x元、1块橡皮y元、1本日记本z元，
根据题意得 13x+5y+2z=31①25x+9y+3z=55②
①×2−②得： x+y+z=7 ，
∴3x+3y+3z=21 ，
答：购买3支铅笔、3块橡皮、3本日记本共需21元.
（3）24
【知识点】解二元一次方程组；三元一次方程组解法及应用
【解析】【解答】解：（1） 3x+2y=7①2x+3y=3②
①-②得 x−y=4 ，
①+②得 5x+5y=10 ，
∴x+y=2 ；
故答案为：4，2；
（3） ∵3∗5=16 ， 2∗3=12 ， x∗y=ax+b+c
∴3a+5b+c=16①2a+3b+c=12②
①-②得 a+2b=4 ，
②×3-①×2得 c−b=4 ，
∴c=b+4 ，
∴5∗9=5a+9b+c=5a+10b+4=5(a+2b)+4=5×4+4=24 .
【分析】（1）方程组中2个方程分别相加、相减即可得出答案；
（2）设购买1支铅笔x元、1块橡皮y元、1本日记本z元 ，利用共需31元和55元列方程组，求得3x+3y+3z=21即可得出答案；
（3） 利用新定义运算 ，得方程组3a+b+c=162a+b+c=12,求得a=4b+c=4,进而结合新定义运算即可5∗9的值.
25．【答案】（1）100°
（2）解： ∠AEF+∠FDC=2∠B .
证明如下：连接 BF ，
∵∠AEF 是 △BFE 的一个外角， ∠FDC 是 △BDF 的一个外角，
∴∠AEF=∠EBF+∠BFE ， ∠FDC=∠BFD+∠FBD ，
由翻折知： ∠EFD=∠ABC ，
∴∠AEF+∠FDC
=∠EBF+∠BFE+∠BFD+∠FBD
=∠EFD+∠ABC
=2∠ABC ；
（3）解：当 BD=BE 时，有 EF//BD .
证明如下：∵BD=BE ，
∴∠BED=∠BDE ，
由翻折知 ∠BED=∠DEF ，
∴∠BDE=∠DEF ，
∴EF//BD ；
（4）∠AEF+2∠B=∠FDC
【知识点】三角形的外角性质；翻折变换（折叠问题）
【解析】【解答】解：（1）∵∠B=50° ，
∴∠BED+∠BDE=130°，
∵△BDE翻折得到△FDE，
∴∠FED+∠FDE=130°，
∴∠AEF+∠FDC=360°−130°−130°=100° ；
故答案为：100°；
（4） ∠AEF+2∠B=∠FDC ；
证明：如图：
∵∠BMD为△EFM外角，
∴∠BMD=∠AEF+∠F，
∵∠FDC为△DMB外角，
∴∠FDC=∠B+∠BMD=∠B+∠F+∠AEF，
∵△BDE翻折得到△FDE，
∴∠F=∠B，
∴∠AEF+2∠B=∠FDC .
【分析】（1）利用三角形的内角和定理算出∠BED+∠BDE=130°，由翻折得∠FED+∠FDE=130°，进而根据平角的定义得出∠AEF+∠FDC=100°；
（2）连接BF，利用三角形的外角等于与它不相邻的两个内角的和得∠AEF=∠EBF+∠BFE， ∠FDC=∠BFD+∠FBD，根据翻折的性质得出 ∠EFD=∠ABC，∠BFD=∠FBD，进行即可得出答案；
（3）当BD=BE时，利用等边对等角得出∠BED=∠BDE，再利用翻折得∠BDE=∠DEF，故可得出∠BDE=∠DEF，然后根据平行线的判定定理即可得出结论；
（4） 数量关系会变，结论：∠AEF+2∠B=∠FDC，理由如下：根据三角形外角的性质得出∠BMD=∠AEF+∠F，∠FDC=∠B+∠BMD=∠B+∠F+∠AEF，根据翻折的性质得出∠F=∠B，从而即可得出结论.32
2
3
1
m
6

3
2
品名
黄瓜
茄子
批发价/（元/千克）
2.4
2.2
零售价/（元/千克）
3.6
3
x（单位：箱）
x<40
40≤x<50
50≤x<60
x≥60
B村村民户数
a
6
5
b
村名
平均数
中位数
众数
A村
48.8
m
59
B村
47.4
45
56