高中数学人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式备课ppt课件

这是一份高中数学人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式备课ppt课件，共28页。PPT课件主要包含了导入新课，精彩课堂，实数根，x10，应用举例，课堂练习，课堂总结等内容，欢迎下载使用。

1.探索与发现问题 什么是一元二次不等式?一般地,我们把只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式.一元二次不等式的一般形式是ax2+bx+c >0或ax2+bx+c <0,其中a,b,c均为常数,a≠0.
探究1 一元二次不等式 x2-12x+20<0的解法(1)解方程2x-7=0;(2)画出函数y=2x-7的图象;(3)解不等式2x-7>0.零点:一元一次方程的解就是相应一次函数的零点,也是一次函数图象与x 轴交点的横坐标.
你能看出这三个题目之间的关系吗?
你能根据一次函数的图象直接看出相应一元一次不等式的解集吗?不等式的解集为函数图象在x轴上方部分对应的横坐标的集合.以上结论能推广到一般的一元一次方程、一次函数、一元一次不等式吗?(1)直线y=ax+b与x轴的交点的横坐标x0是方程ax+b=0的解.(2)作出函数y=ax+b的图象,当a>0时,根据图象得出ax+b>0的解集为{x|x>x0};当a<0时,根据图象得出ax+b>0的解集为{x|x解一元二次不等式 x2-12x+20<0:(1)求一元二次方程 x2-12x+20=0的________, x1=___, x2=____;(2)画函数 y=x2-12x+20的图象;(3)当__________ 时,函数图象位于x轴下方,此时y<0,即x2-12x+20<0.所以,一元二次不等式 x2-12x+20<0的解集为{x|2探究2 二次函数与一元二次方程、不等式的解的对应关系
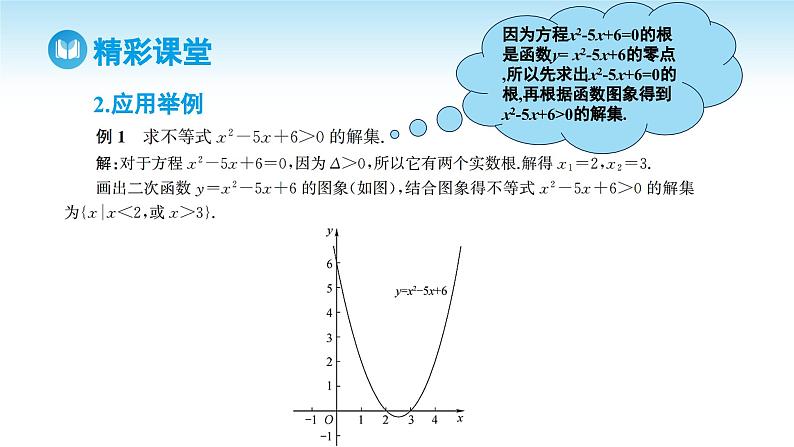
因为方程x2-5x+6=0的根是函数y= x2-5x+6的零点,所以先求出x2-5x+6=0的根,再根据函数图象得到x2-5x+6>0的解集.
你能通过上面三个题目的求解过程,总结一元二次不等式的解题步骤吗?(1)检查二次项系数的符号,将原不等式化成ax2+bx+c>0(a>0)的形式.(2)计算判别式 Δ=b2-4ac的值.如果 Δ≥0,求方程ax2+bx+c=0的根;如果 Δ<0,说明方程ax2+bx+c=0无实数根.(3)画出二次函数y=ax2+bx+c的图象,结合图象得出不等式的解集.
3.利用一元二次不等式解决实际问题
你能总结利用一元二次不等式解决实际问题的一般步骤吗?
(1)由题意列出一元二次不等式; (2)求解一元二次不等式; (3)用求出的结果解释实际问题.
{x|x<-1或 x>5}
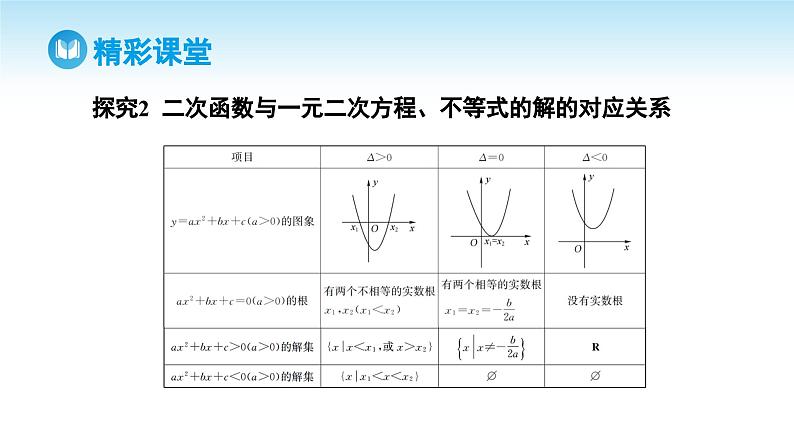
回顾本节课的学习内容并回答下列问题:(1)我们是如何研究解一元二次不等式的?(2)当a>0时,函数y=ax2+bx+c与方程ax2+bx+c=0、不等式ax2+bx+c>0之间有什么关系?(3)请简单说明如何解一元二次不等式ax2+bx+c>0(a>0).(4)利用不等式解决实际问题的一般步骤是什么?(5)利用不等式解决实际问题时应注意哪些问题?