数学选择性必修 第二册1.3 导数在研究函数中的应用同步达标检测题

这是一份数学选择性必修 第二册1.3 导数在研究函数中的应用同步达标检测题，共5页。


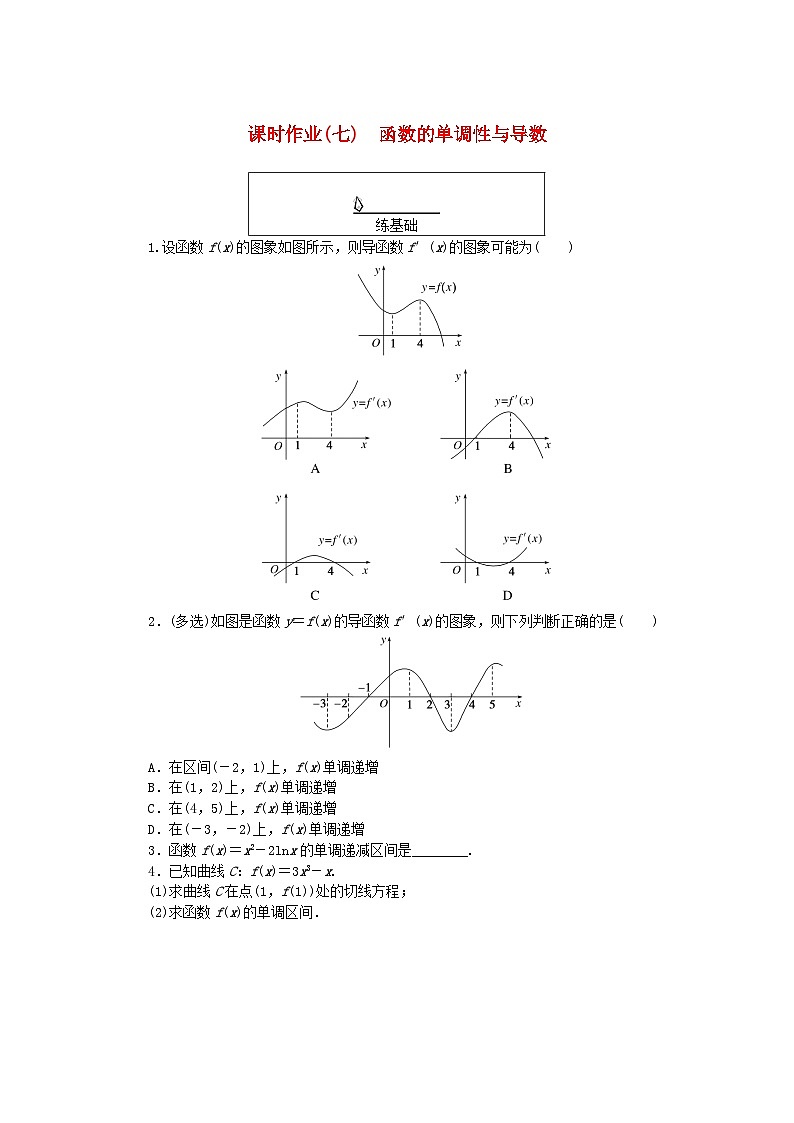
2．(多选)如图是函数y＝f(x)的导函数f′(x)的图象，则下列判断正确的是( )
A．在区间(－2，1)上，f(x)单调递增
B．在(1，2)上，f(x)单调递增
C．在(4，5)上，f(x)单调递增
D．在(－3，－2)上，f(x)单调递增
3．函数f(x)＝x2－2lnx的单调递减区间是________.
4．已知曲线C：f(x)＝3x3－x.
(1)求曲线C在点(1，f(1))处的切线方程；
(2)求函数f(x)的单调区间．
5.(多选)对于函数f(x)＝eq \f(x,lnx)，下列说法错误的是( )
A．f(x)在(1，e)上单调递减，在(e，＋∞)上单调递增
B．f(x)在(0，1)上单调递增，在(1，＋∞)上单调递增
C．f(x)在(0，e)上单调递减，在(e，＋∞)上单调递增
D．f(x)在(0，1)上单调递减，在(e，＋∞)上单调递增
6．在同一坐标系中作出三次函数f(x)＝ax3＋bx2＋cx＋d(a≠0)及其导函数的图象，下列可能正确的序号是( )
A．①②B．①③
C．③④D．①④
7．若函数f(x)＝(x2＋mx)ex的单调递减区间是[－eq \f(3,2)，1]，则实数m的值为________，函数f(x)的单调递增区间是________________．
8．设函数f(x)＝ex－ax－2，求f(x)的单调区间．
9．已知函数f(x)＝x＋eq \f(a,x)＋b(x≠0)，其中a，b∈R.
(1)若曲线y＝f(x)在点P(2，f(2))处的切线方程为y＝3x＋1，求a，b的值；
(2)若函数f(x)在(1，2)上为单调函数，求实数a的取值范围．
10.函数f(x)在x>0上可导且满足xf′(x)－f(x)>0，则下列一定成立的为( )
A．eq \f(f（π）,π)>eq \f(f（e）,e)B．f(π)C．eq \f(f（π）,π)f(e)
11．已知函数f(x)＝lnx＋ax(a∈R).
(1)当a＝1时，求曲线y＝f(x)在x＝1处的切线方程；
(2)求函数f(x)的单调区间．
课时作业(七) 函数的单调性与导数
1．解析：∵f(x)在(－∞，1)，(4，＋∞)上单调递减，在(1，4)上是单调递增，
∴当x＜1或x＞4时，f′(x)＜0；
当1＜x＜4时，f′(x)＞0.
答案：C
2．解析：由题图知当x∈(－2，1)时，f′(x)有正有负，故f(x)在(－2，1)上不单调，故A错误；当x∈(1，2)，x∈(4，5)时，f′(x)>0，所以在(1，2)，(4，5)上，f(x)是单调递增，故B、C正确；当x∈(－3，－2)时，f′(x)<0，所以在(－3，－2)上，f(x)是单调递减，故D错误．
答案：BC
3．解析：函数f(x)＝x2－2lnx的定义域为(0，＋∞)，由f′(x)＝2x－eq \f(2,x)＝eq \f(2x2－2,x)<0，可得0答案：(0，1)
4．解析：(1)由f(x)＝3x3－x，可得f′(x)＝9x2－1，
故由f(x)在点(1，f(1))处切线的斜率k＝f′(1)＝8，
又f(1)＝2，
所以所求切线方程为y－2＝8(x－1)，即8x－y－6＝0.
(2)因为f′(x)＝9x2－1，
令f′(x)＝9x2－1>0，则x<－eq \f(1,3)或x>eq \f(1,3)，
令f′(x)＝9x2－1<0，则－eq \f(1,3)故f(x)的单调增区间为(－∞，－eq \f(1,3))，(eq \f(1,3)，＋∞)；单调减区间为(－eq \f(1,3)，eq \f(1,3)).
5．解析：f′(x)＝eq \f(lnx－1,（lnx）2)＝0，x>0且x≠1，得x＝e，
当x∈(0，1)∪(1，e)时，f′(x)<0，所以函数f(x)的单调递减区间是(0，1)和(1，e)，
当x∈(e，＋∞)时，f′(x)>0，函数f(x)的单调递增区间是(e，＋∞).
答案：BC
6．解析：根据f′(x)>0时，y＝f(x)递增，f′(x)<0时，y＝f(x)递减可得，①②中函数的图象的增减趋势与导函数的正负区间是吻合的，可能正确；而③中导函数为负的区间内相应的函数不为递减，故错误，④中导函数为负的区间内相应的函数不为递减，故错误．
答案：A
7．解析：f′(x)＝[x2＋(m＋2)x＋m]ex，
因为f(x)的单调递减区间是[－eq \f(3,2)，1]，
所以f′(x)＝0的两个根分别为x1＝－eq \f(3,2)，x2＝1，
即eq \b\lc\{(\a\vs4\al\c1(f′\b\lc\(\rc\)(\a\vs4\al\c1(－\f(3,2)))＝0，,f′（1）＝0，))解得m＝－eq \f(3,2).
由f′(x)＝(x2＋eq \f(1,2)x－eq \f(3,2))ex＝eq \f(1,2)(x－1)(2x＋3)ex，
得f′(x)>0时，x<－eq \f(3,2)或x>1.
答案：－eq \f(3,2) (－∞，－eq \f(3,2))，(1，＋∞)
8．解析：f(x)的定义域为(－∞，＋∞)，f′(x)＝ex－a.
若a≤0，则f′(x)>0，所以f(x)在(－∞，＋∞)上单调递增．
若a>0，则当x∈(－∞，lna)时，f′(x)<0；当x∈(lna，＋∞)时，f′(x)>0.
所以f(x)在(－∞，lna)上单调递减，在(lna，＋∞)上单调递增．
综上所述，当a≤0时，函数f(x)在(－∞，＋∞)上单调递增；
当a>0时，f(x)在(－∞，lna)上单调递减，在(lna，＋∞)上单调递增．
9．解析：(1)f′(x)＝1－eq \f(a,x2)，由导数的几何意义得f′(2)＝3⇒1－eq \f(a,4)＝3，
于是a＝－8，
由切点P(2，f(2))在直线y＝3x＋1上可得－2＋b＝7，解得b＝9.
(2)∵函数f(x)在(1，2)上为单调函数，
①若f(x)在(1，2)上为单调递增函数，则f′(x)≥0.当x∈(1，2)恒成立，∴x2－a≥0，即a≤x2；当x∈(1，2)恒成立，∴a≤1；
②若f(x)在(1，2)上为单调递减函数，则f′(x)≤0.当x∈(1，2)恒成立，∴x2－a≤0，即a≥x2；当x∈(1，2)恒成立，a≥4.
综上所述，a≤1或a≥4.
10．解析：令F(x)＝eq \f(f（x）,x)，则F′(x)＝eq \f(xf′（x）－f（x）,x2)，根据题意，当x>0时，xf′(x)－f(x)>0，即F′(x)>0，故F(x)在(0，＋∞)上单调递增，则F(π)>F(e)，即eq \f(f（π）,π)>eq \f(f（e）,e).
答案：A
11．解析：(1)a＝1时，f(x)＝lnx＋x，
则f′(x)＝eq \f(1,x)＋1，f(1)＝1，f′(1)＝2，
故切线方程为y－1＝2(x－1)，即2x－y－1＝0.
(2)函数f(x)＝lnx＋ax(a∈R)的定义域为(0，＋∞)；
f′(x)＝eq \f(1＋ax,x)，
①当a≥0时，f′(x)＝eq \f(1＋ax,x)>0，
则函数f(x)＝lnx＋ax(a∈R)在(0，＋∞)上单调递增；
②当a<0时，x∈(0，－eq \f(1,a))时，f′(x)>0，
则函数f(x)＝lnx＋ax(a∈R)在(0，－eq \f(1,a))上单调递增；
x∈(－eq \f(1,a)，＋∞)时，f′(x)<0，
则函数f(x)＝lnx＋ax(a∈R)在(－eq \f(1,a)，＋∞)上单调递减．
综上所述，当a≥0时，函数f(x)的单调递增区间为(0，＋∞)；
当a<0时，函数f(x)的单调递增区间为(0，－eq \f(1,a))；单调递减区间为(－eq \f(1,a)，＋∞).
练基础
提能力
培优生