





人教版九年级下册28.1 锐角三角函数备课课件ppt
展开互余的两角之间的三角函数值之间的关系: 若∠A +∠B = 90°,则 sinA csB,csA sinB, tanA · tanB = .
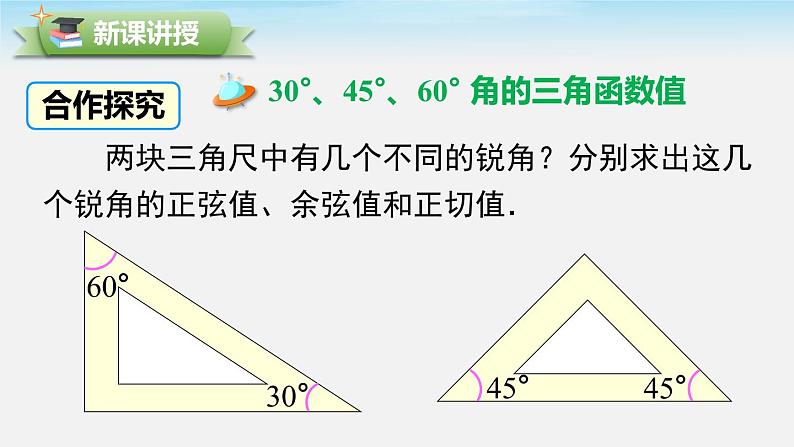
30°、45°、60° 角的三角函数值
两块三角尺中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
如图,设 30° 角所对的直角边长为 a,那么斜边长为 2a,
如图,设两条直角边长为 a,则斜边长为
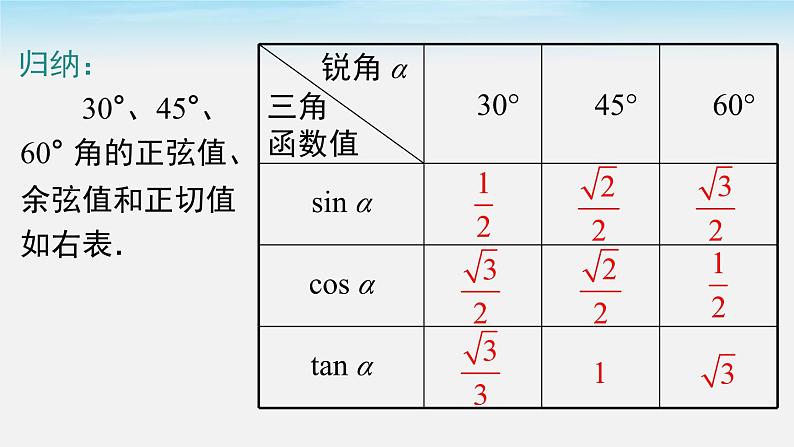
30°、45°、60° 角的正弦值、余弦值和正切值如右表.
例 1 求下列各式的值:
提示:cs260° 表示(cs60°)2,即 (cs60°)×(cs60°).
解:cs260° + sin260°
(1) cs260° + sin260°;
计算:(1) sin30° + cs45°;
(2) sin230° + cs230°-tan45°.
求满足下列条件的锐角 α .
(1) 2sinα - = 0; (2) tanα-1 = 0.
(2) tanα =1, ∴ α = 45°.
例 3 已知 △ABC 中的∠A 与锐角∠B 满足 (1-tanA)2 +|sinB- |=0,试判断 △ABC 的形状.
∴ tanA=1,sinB=∴∠A=45°,锐角∠B=60°.∴∠C=180°-45°-60°=75°.∴△ABC 是锐角三角形.
∴ tanB= ,sinA= .∴∠B=60°,∠A=60°.
2. 已知 α 为锐角,且 tanα 是方程 x2 + 2x -3 = 0 的一 个根,求 2sin2α + cs2α - tan(α + 15°) 的值.
解:解方程 x2 + 2x-3 = 0,得 x1 = 1,x2 =-3. ∵ α 为锐角,tanα>0,∴ tanα = 1. ∴ α = 45°. ∴ 2sin2α + cs2α - tan (α + 15°) = 2sin245° + cs245°- tan60°
1. tan (α + 20°)=1,锐角 α 的度数应是 ( ) A. 40° B. 30° C. 20° D. 10°
A. csA = B. csA =C. tanA = 1 D. tanA =
3. 在 △ABC 中,若 ,则 ∠C = °.
4. 如图,以 O 为圆心,任意长为半径 画弧,与射线 OA 交于点 B,再以 B 为圆心,BO 长为半径画弧,两弧交 于点 C,画射线 OC,则 sin∠AOC 的值为 .
5. 求下列各式的值: (1) 1-2 sin30°cs30°; (2) 3tan30°-tan45° + 2sin60°; (3) ; (4)
解:过点 C 作 CD⊥AB 于点 D.
∴ AB = AD + BD = 3 + 2 = 5.
数学九年级下册28.2 解直角三角形及其应用课文课件ppt: 这是一份数学九年级下册28.2 解直角三角形及其应用课文课件ppt,共16页。PPT课件主要包含了情境引入,新知探究,新知学习,特殊角的三角函数值,例题讲解,巩固提高,总结提升,布置作业等内容,欢迎下载使用。
人教版九年级下册28.1 锐角三角函数教学ppt课件: 这是一份人教版九年级下册28.1 锐角三角函数教学ppt课件,共15页。PPT课件主要包含了教学目标,教学重难点,教学设计,活动4例题与练习,求下列各式的值,解在图中,活动5等内容,欢迎下载使用。
人教版九年级下册28.1 锐角三角函数教课内容ppt课件: 这是一份人教版九年级下册28.1 锐角三角函数教课内容ppt课件,共22页。PPT课件主要包含了复习引入,sinA,cosA,tanA,合作探究,另一条直角边长为,典例精析,练一练,解原式,通过三角函数值求角度等内容,欢迎下载使用。













