期河南省南阳市南召县2023-2024学年数学八年级第一学期期末复习检测模拟试题含答案

这是一份期河南省南阳市南召县2023-2024学年数学八年级第一学期期末复习检测模拟试题含答案，共6页。试卷主要包含了点P，不等式﹣2x＞的解集是，若，则的值是等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
一、选择题（每题4分，共48分）
1．以二元一次方程组的解为坐标的点在平面直角坐标系的（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
2．下列命题是假命题的是
A．同旁内角互补，两直线平行
B．若两个数的绝对值相等，则这两个数也相等
C．平行于同一条直线的两条直线也互相平行
D．全等三角形的周长相等
3．在平面直角坐标系中，直线与直线交与点，则关于，的方程组的解为（ ）‘
A．B．C．D．
4．不能判定一个四边形是平行四边形的条件是（ ）
A．两组对边分别平行B．一组对边平行，另一组对边相等
C．一组对边平行且相等D．两组对边分别相等
5．点P（﹣1，2）关于x轴对称点的坐标为（ ）
A．（1，﹣2） B．（﹣1，2） C．（1，2） D．（﹣1，﹣2）
6．不等式﹣2x＞的解集是（ ）
A．x＜﹣B．x＜﹣1C．x＞﹣D．x＞﹣1
7．下列四个图案中，是轴对称图形的是（ ）
A．B．C．D．
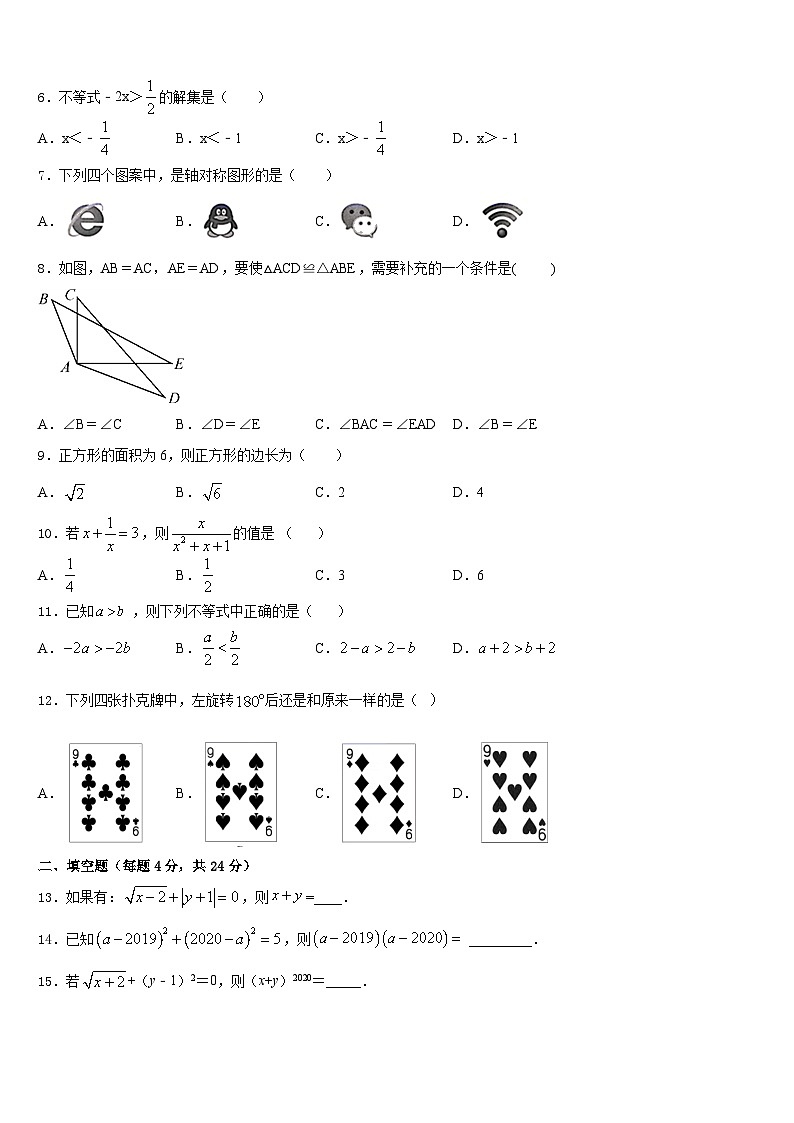
8．如图，AB＝AC，AE＝AD，要使△ACD≌△ABE，需要补充的一个条件是( )
A．∠B＝∠CB．∠D＝∠EC．∠BAC＝∠EADD．∠B＝∠E
9．正方形的面积为6，则正方形的边长为（ ）
A．B．C．2D．4
10．若，则的值是 （ ）
A．B．C．3D．6
11．已知 ，则下列不等式中正确的是（ ）
A．B．C．D．
12．下列四张扑克牌中，左旋转后还是和原来一样的是（ ）
A．B．C．D．
二、填空题（每题4分，共24分）
13．如果有：，则=____．
14．已知，则 _________．
15．若+（y﹣1）2＝0，则（x+y）2020＝_____．
16．已知，则的值为____．
17．甲、乙二人做某种机械零件,己知甲每小时比乙多做6个，甲做90个零件所用的时间与乙做60个零件所用的时间相等．设甲每小时做x个零件，依题意列方程为_________．
18．______；_____.
三、解答题（共78分）
19．（8分）分解因式：
（1）ax2﹣9a；
（2）4ab2﹣4a2b﹣b1．
20．（8分）如图，在长方形ABCO中，点O为坐标原点，点B的坐标为（8，6），点A，C在坐标轴上，直线y=2x+b经过点A且交x轴于点F．
（1）求b的值和△AFO的面积；
（2）将直线y=2x+b向右平移6单位后交AB于点D，交y轴于点E；
①求点D，E的坐标；
②动点P在BC边上，点Q是坐标平面内第一象限内的点，且在平移后的直线上，若△APQ是等腰直角三角形，求点Q的坐标．
21．（8分）阅读以下材料：
对数的创始人是苏格兰数学家纳皮尔（J.Napier，1550-1617年），纳皮尔发明对数是在指数书写方式之前，直到18世纪瑞士数学家欧拉（Euler，1707-1783年）才发现指数与对数之间的联系，对数的定义：一般地，若，那么x叫做以a为底N的对数，记作：，比如指数式可以转化为，对数式可以转化为，我们根据对数的定义可得到对数的一个性质： )，理由如下：
设则
∴，由对数的定义得
又∵，
所以，解决以下问题：
（1）将指数转化为对数式____；计算___；
（2）求证：
（3）拓展运用：计算
22．（10分）如图，已知BD是△ABC的角平分线，点E、F分别在边AB、BC上，ED∥BC，EF∥AC．求证：BE=CF．
23．（10分）大石桥市政府为了落实“暖冬惠民工程”，计划对城区内某小区的部分老旧房屋及供暖管道和部分路段的人行地砖、绿化带等公共设施进行全面更新改造．该工程乙队单独完成所需天数是甲队单独完成所需天数的1.5倍 ， 若甲队先做10天，剩下两队合作30天完成．
（1）甲乙两个队单独完成此项工程各需多少天？
（2）已知甲队每天的施工费用为8.4万元，乙对每天的施工费用为5.6万元，工程施工的预算费用为500万元，为了缩短工期并高效完成工程，拟预算的费用是否够用？若不够用，需追加预算多少万元？请说明理由．
24．（10分）如图，在长方形纸片中，．将其折叠，使点与点重合，点落在点处，折痕交于点，交于点．
（1）求线段的长．
（2）求线段的长．
25．（12分）如图1，两个不全等的等腰直角三角形和叠放在一起，并且有公共的直角顶点.
（1）在图1中，你发现线段的数量关系是______．直线相交成_____度角．
（2）将图1中绕点顺时针旋转90°，连接得到图2，这时（1）中的两个结论是否成立？请作出判断说明理由．
26．（12分）某汽车制造厂生产一款电动汽车，计划一个月生产200辆．由于抽调不出足够的熟练工来完成电动汽车的安装，工厂决定招聘一些新工人，他们经过培训后上岗，也能独立进行电动汽车的安装．生产开始后，调研部门发现：1名熟练工和2名新工人每月可安装8辆电动汽车；2名熟练工和3名新工人每月可安装14辆电动汽车．
（1）每名熟练工和新工人每月分别可以安装多少辆电动汽车？
（2）若工厂现在有熟练工人30人，求还需要招聘多少新工人才能完成一个月的生产计划？
参考答案
一、选择题（每题4分，共48分）
1、A
2、B
3、A
4、B
5、D
6、A
7、D
8、C
9、B
10、A
11、D
12、C
二、填空题（每题4分，共24分）
13、1
14、1
15、1
16、1
17、＝
18、5 2
三、解答题（共78分）
19、（1）a（x+1）（x﹣1）；（2）﹣b（2a﹣b）2．
20、（1）b=6，S△ADO=×3×6=；（2）①D(6，6)，E(0，-6)；②点Q的坐标可以为(,)，(4，2)，(，).
21、（1），3；（2）证明见解析；（3）1
22、证明见解析．
23、（1）甲队单独完成此项工程需要1天，乙队单独完成此项工程需要2天；（2）工程预算的施工费用不够用，需追加预算4万元．
24、（1）1；（2）1．
25、 (1)AC=BD，直线相交成90°；(2)结论成立,详见解析.
26、（1）每名熟练工每月可以按装4辆电动汽车，每名新工人每月可以按装2辆电动汽车；（2）1名