

(期末押题卷)期末解决问题-广东省广州市2023-2024学年六年级上学期数学高频易错期末预测必刷卷(人教版)
展开2.甲数是乙数的34,丙数是甲数的25,那么丙数是乙数的几分之几?
3.防疫站给学校捐赠49箱防疫口罩,其中47是儿童型口罩,儿童型口罩有多少箱?
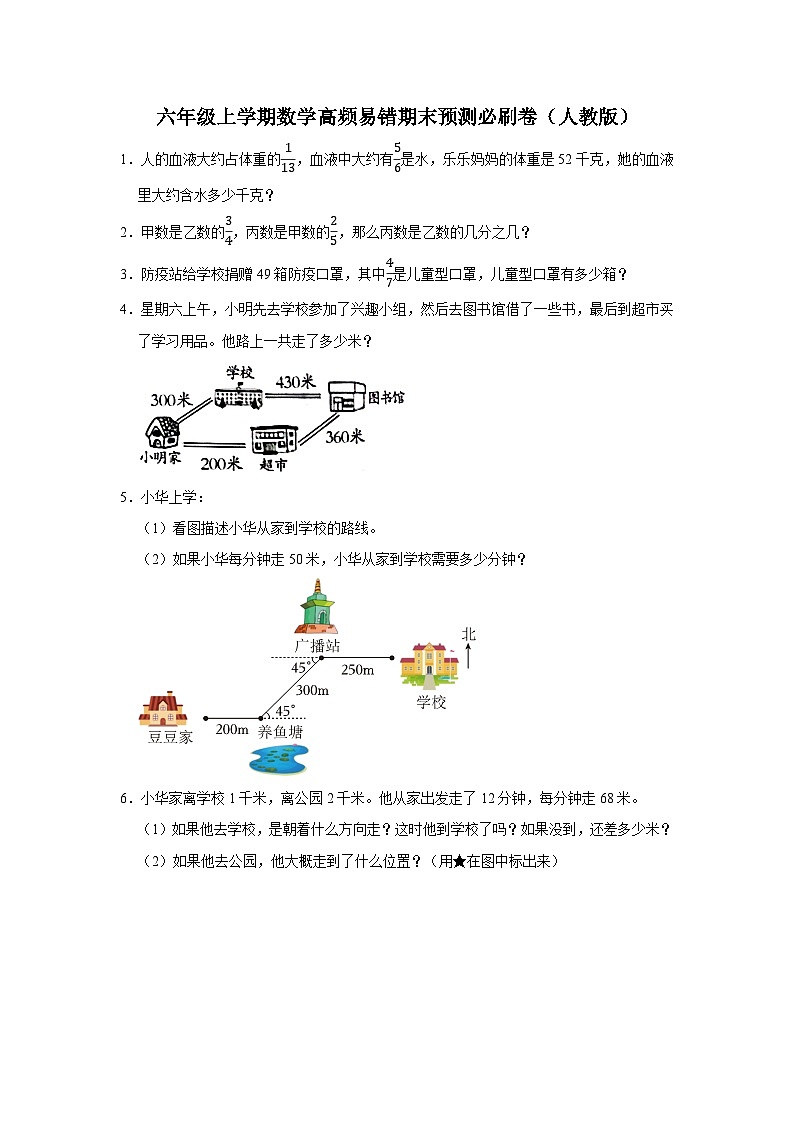
4.星期六上午,小明先去学校参加了兴趣小组,然后去图书馆借了一些书,最后到超市买了学习用品。他路上一共走了多少米?
5.小华上学:
(1)看图描述小华从家到学校的路线。
(2)如果小华每分钟走50米,小华从家到学校需要多少分钟?
6.小华家离学校1千米,离公园2千米。他从家出发走了12分钟,每分钟走68米。
(1)如果他去学校,是朝着什么方向走?这时他到学校了吗?如果没到,还差多少米?
(2)如果他去公园,他大概走到了什么位置?(用★在图中标出来)
7.工程队要种400棵树苗,如果让甲队单独做需要8天,如果让乙队单独做需要10天。现在要求5天完成,两队合种,能完成吗?
8.某工程队要修一条1200米长的公路。若甲队单独修需要24天完成,乙队单独修需要20天完成,两队一起合修,需要几天完成?
9.工程队要修一条长975米的公路,已经修了15天,还剩下45米没有修,平均每天修多少米?
10.修路队修一条公路,前3天修了22.5千米,照这样计算,再有8天可以完工,这条路全长多少千米?
11.加工一批零件,师傅单独做完要6小时,徒弟单独做完要8小时。照这样计算,师徒两人同时合作,需要多少小时完成?
12.甲工程队5.4小时修路126.9m,乙工程队3.5小时修路97.3m。哪个工程队修得快一些?每小时多修多少米?
13.六年级一班男女生人数比是9:7,,已知男生比女生多6人,六年级一班一共有多少人?
14.甲、乙两地相距690千米,一列快车和一列慢车同时从两地相向而行,3小时相遇。两车的速度比是12:11,快车和慢车每小时各行多少千米?
15.小强一家假期去北京旅游,第一天行了总路程的25,第二天行了90千米,已经行的路程与剩下的路程的比是5:3。那么小强他们从家到北京全程有多少千米?
16.甲、乙两筐苹果共重135千克,甲、乙两筐苹果的质量比是5:4。甲、乙两筐苹果各有多少千克?
17.向阳小学进行书法比赛,比赛的学生共有125人。低年级人数是中年级的58,中年级与高年级人数比是2:3,中年级参加书法比赛的有多少人?
18.小明看一本连环画,上午看了14,下午又看了21页,这时已看的页数与未看的页数比是3:2,这本连环画一共有多少页?
19.一张圆形桌面的直径是12dm,它的周长是多少分米?它的面积是多少平方分米?
20.量得圆形羊圈的周长是188.4米。这个羊圈的面积是多少平方米?
21.军军在探究圆的面积计算公式时,用到了下面的方法:先将圆平均分成32分,再拼成一个近似的长方形(如图所示)。军军量得这个长方形的宽是3厘米,请你帮军军计算出这个圆的面积。
22.王大妈用篱笆靠墙围了一个菜地,它由一个正方形和一个半圆形组成(如图)。篱笆长多少米?这个菜地的占地面积是多少平方米?
23.公园里有一个半径是10m的圆形人工湖,现要在这个人工湖的周围修一条宽为2m的环形小路,这条小路的面积是多少平方米?
24.如图是表示王大伯家三种蔬菜种植情况的统计图。其中青菜种了90平方米。请计算出王大伯家萝卜种植了多少平方米?
25.近年来,各地“广场舞”噪音干扰的问题倍受关注。相关人员对本地区15~65岁年龄段的市民进行了随机调查,并制作了如下相应的统计图。市民对“广场舞”噪音干扰的态度有以下五种:A.没影响B.影响不大C.有影响,建议做无声运动D.影响很大,建议取缔E.不关心这个问题。
根据以上信息解答下列问题:
(1)根据统计图填空:m= 。
(2)在此次调查中,“不关心这个问题”的有25人,请问一共调查了 人。
(3)在此次调查中,持“影响不大”态度的人比持“没影响”态度的人多百分之 。
26.小强家6月份生活开支情况如图,如果水电支出200元,那么:
(1)赡养老人支出多少元?
(2)食品支出多少元?
27.华地商场根据2021年冰箱销售情况绘制了以下两幅不完整的统计图:
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)华地商场2021年一共销售冰箱 台。
(2)补全条形统计图中第二季度和第四季度的信息。
(3)经过市场调查,一般购买冰箱的消费者大多为将要结婚的夫妇。今年5月,华地商场收集了如下信息:
据官方统计,2022年5月20日当天,全国婚姻登记机构共计办理结婚登记31.25万对。《结婚产业观察》整理汇编了山东、四川、广东、湖北、湖南、江苏等18个省市的数据,截止5月21日13点,5月20日单日累计办理结婚登记近20万对。
如果你是华地商场经理,打算2023年要搞一次冰箱销售促销活动,请你结合以上数据信息,把明年商场促销方案的两个信息补充完整。
华地商场2023年冰箱销售促销方案(部分)
促销时间:
说明选择这个时间的理由:
备货数量:
说明预估这些数量的理由:
28.如图所示:下面是配制某种混凝土时,所需要的材料质量情况统计图,现有3.6吨的水泥。
(1)能配制多少吨这样的混凝土?
(2)河沙比石子少多少吨?
29.某校调查全校学生视力情况,三个学段学生近视人数占全校近视总人数百分比如图。该校学生总数为800人,全校近视的学生是360人。
(1)低年级学段学生近视人数占全校学生近视人数的 %。
(2)高年级近视学生有多少人?
(3)全校学生近视率是多少?
30.一张桌子可以坐6个人,两张桌子拼起来可以坐10个人,那么9张桌子像这样拼起来可以坐多少人?
31.小明用面积为1cm2的正方形卡纸拼摆图形.
(1)像这样拼下去,第(5)个图形要用多少张小正方形卡纸?
(2)如果要在第n个图形的外围用铁丝镶上一圈边框,至少需要多少厘米铁丝?
32.用小棒按照如图的方式摆图形.
(1)摆1个五边形需要 根小棒,摆2个五边形需要 根小棒,摆3个五边形需要 根小棒.
(2)照这样摆下去,
①摆5个五边形需要多少根小棒?摆10个呢?
②用61根小棒可以摆出多少个五边形?
33.按照前两组的规律填数,你知道第三组的“?”处应该填几吗?
34.修一条水渠,第一天修的与未修的比是2:7,如果再修50米,正好修完了一半,这条水渠长多少米?
35.一批零件,平均分给师徒两人加工,师傅和徒弟每小时加工零件个数的比是8:5,当师傅完成任务时,徒弟还有75个没有完成。这批零件一共有多少个?
36.实验小学即将隆重举行“喜迎元旦暨十周年校庆”活动,六(6)班也在紧锣密鼓地筹备班级活动。六名女生负责布置本班教室环境,其中小月和小玉负责挂彩带。小月单独挂彩带需要20分钟,小玉单独挂彩带需要30分钟。两人合作同时挂彩带,目前小月已经挂了24根彩带,小玉挂的彩带数量比小月少13,如果两人一共再挂16根彩带,则已挂与剩下的彩带数量比是7:2。经过大家的共同努力,教室环境焕然一新,洋溢着节日喜庆的气氛。
(1)小月和小玉的工作效率的比是 。
(2)如果两人同时挂彩带,一共需要多少分钟才能完成任务?
(3)六(6)教室一共要挂多少根彩带?
37.甲、乙两个仓库所存面粉质量的比是3:7。如果从乙仓库调2500kg面粉存入甲仓库,这时甲仓库面粉的质量是乙仓库的23。甲、乙两个仓库原来各存面粉多少千克?
38.水果超市运来香蕉、苹果和梨一共270千克,香蕉和苹果的质量之比是5:6。梨的质量比苹果的12少10千克。水果超市运来的香蕉、苹果和梨各有多少千克?
39.我国地形复杂多样,既有广阔的平原和低缓的丘陵,也有雄伟的高原和起伏的山地,还有中间低四周高的盆地。我国陆地领土各种地形所占百分比如图。
(1)如果把山地、丘陵和高原的地区统称为山区,那么我国山区的面积占到全国陆地面积的 %。
(2)已知我国平原的面积约115.2万平方千米,我国陆地领土面积约多少万平方千米?
六年级上学期数学高频易错期末预测必刷卷(人教版)
参考答案与试题解析
1.【答案】103千克。
【分析】将乐乐妈妈的体重看作单位“1”,先用52乘113,求出乐乐妈妈体内血液的千克数;再乘56,即可求出她的血液里大约含水多少千克。
【解答】解:52×113×56
=4×56
=103(千克)
答:她的血液里大约含水103千克。
【点评】求一个数的几分之几是多少,用乘法计算。
2.【答案】310。
【分析】根据题意,把乙数看作单位“1”,甲数是乙数的34,丙数是甲数的25,可以分别求出甲数和乙数,再根据求一个数是另一个数的几分之几用除法,即可解答。
【解答】解:把乙数看作单位“1”,甲数是乙数的34,丙数是甲数的25
所以甲数:1×34=34
丙数:34×25=310
310÷1=310
答:丙数是乙数的310。
【点评】熟练掌握求一个数是另一个数的几分之几用除法是解题的关键。
3.【答案】28箱。
【分析】把学校捐赠防疫口罩箱数看作单位“1”,总箱数乘儿童型口罩对应的分率即可求解。
【解答】解:49×47=28(箱)
答:儿童型口罩有28箱。
【点评】本题主要考查了分数乘法的应用题,解题的关键是找出单位“1”及对应分率。
4.【答案】1090米。
【分析】将小明家到学校的距离加上学校到图书馆的距离,再加上图书馆到超市的距离,即可解答。
【解答】解:300+430+360
=730+360
=1090(米)
答:他路上一共走了1090米。
【点评】本题考查千以内加法的计算及应用。理解题意,找出数量关系,列式计算即可。
5.【答案】(1)小华从家出发,先向东走200米到养鱼塘,然后向东偏北45°走300米到广播站,再向东走250米到学校。
(2)15分钟。
【分析】(1)根据上北下南、左西右东的方法辨别方向,利用标出的距离,结合图上所给角度,描述小华从家到学校的路线即可。
(2)计算小华所行路程,然后利用公式:时间=路程÷速度,计算时间即可。
【解答】解:(1)小华从家出发,先向东走200米到养鱼塘,然后向东偏北45°走300米到广播站,再向东走250米到学校。
(2)(200+300+250)÷50
=750÷50
=15(分钟)
答:小华从家到学校需要15分钟。
【点评】本题主要考查线路图,关键是根据图上确定方向的方法确定方向,结合标出的距离,完成线路图的描述。
6.【答案】(1)朝着正东方向走,这时他没到学校,还差184米。
(2)。
【分析】(1)根据平面图上方向的辨别“上北下南,左西右东”,小华如果去学校,朝着正东方向走。根据“路程=速度×时间”,即可求出小华走的路程,根据计算结果即可确定是否到学校,如果没到,进而求出还差的米数。
(2)由(1)计算可知,此题小华走了816米,不到1千米,小华家到公园是2米,他大概的位置不到一半,且接近一半。
【解答】解:(1)如果他去学校,是朝着正东方向走
68×12=816米
1千米=1000米
816米<1000米
这时他没到学校
1000﹣816=184(米)
答:如果他去学校,是朝着正东方向走,这时他没到学校,还差184米。
(2)由以上计算可知,此时小华走了816米,他大概的位置不到一半,且接近一半(下图)。
【点评】此题考查的知识点:路程、速度、时间三者之间的关系;方向;根据方向和距离确定物体的位置等。
7.【答案】能完成。
【分析】把种这批树苗的总数看作单位“1”,则甲队的工作效率是18,乙队的工作效率是110,再根据工作时间=工作总量÷甲乙的工作效率和,求出完成的时间,再与5进行比较即可。
【解答】解:1÷(18+110)
=1÷940
=449(天)
449<5
答:能完成。
【点评】本题考查工程问题的解题方法,解题关键是要把工作总量看作单位“1”,利用工作时间=工作总量÷甲乙的工作效率和,求出完成的时间。
8.【答案】12011天。
【分析】根据“工作效率=工作量÷工作时间”,求出两队的工作效率,再根据“工作时间=工作量÷工作效率和”,即可解答。
【解答】解:1200÷(1200÷24+1200÷20)
=1200÷(50+60)
=1200÷110
=12011(天)
答:两队一起合修,需要12011天完成。
【点评】本题考查的是工程问题,掌握“工作效率=工作量÷工作时间”,“工作时间=工作量÷工作效率和”,是解答关键。
9.【答案】62米。
【分析】用975米减去45米,求出已经修了多少米,再根据工作效率=工作量÷工作时间,即可解答。
【解答】解:(975﹣45)÷15
=930÷15
=62(米)
答:平均每天修62米。
【点评】本题考查的是工程问题,掌握工作效率=工作量÷工作时间是解答关键。
10.【答案】见试题解答内容
【分析】“照这样计算”说明每天的工作效率相同;先用前3天的工作量除以3天,求出工作效率,然后再用工作效率乘上总工作时间11天,解答即可.
【解答】解:22.5÷3×(3+8)
=7.5×11
=82.5(千米)
答:这条路全长82.5千米.
【点评】解答此题的关键是先求得单一量,再由不变的单一量求得总量.
11.【答案】247小时。
【分析】把加工一批零件的工作量看作单位“1”,根据工作效率=工作量÷工作时间,分别求出两人的工作效率,再根据工作时间=工作量÷工作效率和,即可解答。
【解答】解:1÷(16+18)
=1÷724
=247(小时)
答:需要247小时完成。
【点评】本题考查的是工程问题,掌握工作效率=工作量÷工作时间,工作时间=工作量÷工作效率和是解答关键。
12.【答案】乙工程队;每小时多修4.3米。
【分析】修路效率=修路长度÷修路时间,由此计算出两队的修路效率,然后比较大小。
【解答】解:甲工程队:126.9÷5.4=23.5(米/时)
乙工程队:97.3÷3.5=27.8(米/时)
27.8>23.5
27.8﹣23.5=4.3(米/时)
答:乙工程队修得快一些,每小时多修4.3米。
【点评】本题考查的是工程问题的应用。
13.【答案】48人。
【分析】用9﹣7=2(份),求出男生比女生多2份,这个2份就是6人,用6除以2,求出1份是多少,再分别乘份9和7份,分别求出男生和女生人数,再相加即可解答。
【解答】解:9﹣7=2(份)
6÷2=3(人)
3×9=27(人)
3×7=21(人)
27+21=48(人)
答:六年级一班一共有48人。
【点评】本题考查的是比的应用,求出1份是多少是解答关键。
14.【答案】120千米;110千米。
【分析】先用路程除以相遇时间求出快车与慢车的速度和,把速度和按12:11的比分配,即用速度和除以份数和,求出1份的路程,再用1份的路程分别乘各自的份数,即可求出各自的速度。
【解答】解:690÷3=230(千米)
230÷(12+11)
=230÷23
=10(千米)
10×12=120(千米)
10×11=110(千米)
答:快车每小时行120千米;慢车每小时行110千米。
【点评】本题考查的是比的应用,关键是:把比看作分得的份数,先求出总份数,再求出每一份是多少,最后求出各部分相应的具体数量。
15.【答案】400千米。
【分析】根据已经行的路程与剩下的路程的比是5:3可知已经行的路程占总路程的55+3=58,则第二天行驶的路程占了全程的(58−25),则根据第二天行驶的实际路程90,用90除以第二天行驶占全程的分率即可求出全程长。
【解答】解:55+3−25=940
90÷940=400(千米)
答:小强他们从家到北京全程有400千米。
【点评】本题主要考查了比的应用。
16.【答案】甲筐75千克,乙筐60千克。
【分析】用苹果总重乘甲筐的所占的份数即可求出甲筐的质量,用总质量减甲筐的质量即可求出乙筐的质量,据此求解。
【解答】解:135×55+4=75(千克)
135﹣75=60(千克)
答:甲筐苹果有75千克,乙筐苹果有60千克。
【点评】本题主要考查了比的应用。
17.【答案】40人。
【分析】由。低年级人数是中年级的58,可知,底年级人数与中年级人数的比是5:8,把中年级与高年级人数比的前、后项都乘4,即可写出低、中、高年级人数的连比,根据连比求出中年级人数所占的分率,然后根据分数乘法的意义解答。
【解答】解:低、中年级人数的比:58=5:8
中、高年级人数的比:2:3=8:12
底、中、高年级人数的比:5:8:12
125×85+8+12
=125×825
=40(人)
答:中年级参加书法比赛的有40人。
【点评】解答此题的关键是根据题意写出低、中、高三个年级的人数比,再把比转化成分数,然后根据分数乘法的意义解答。
18.【答案】60页。
【分析】设这本连环画一共有x页,用已看的页数:未看的页数=3:2,列出比例,即可解答。
【解答】解:(14x+21):(x−14x﹣21)=3:2
(14x+21)×2=(x−14x﹣21)×3
12x+42=94x﹣63
74x=105
x=60
答:这本连环画一共有60页。
【点评】本题考查的是比的应用,掌握用已看的页数:未看的页数=3:2,列出比例是解答关键。
19.【答案】37.68分米,113.04平方分米。
【分析】圆的半径=直径÷2,圆的周长=3.14×直径,圆的面积=3.14×半径×半径,结合题中数据计算即可。
【解答】解:圆的半径:12÷2=6(分米)
3.14×12=37.68(分米)
3.14×6×6=113.04(平方分米)
答:它的周长是37.68分米,面积是113.04平方分米。
【点评】本题考查的是圆的周长、面积公式的应用。
20.【答案】2826平方米。
【分析】根据圆的周长公式:C=2πr,那么r=C÷π÷2,据此求出半径,再根据圆的面积公式:S=πr2,把数据代入公式解答。
【解答】解:3.14×(188.4÷3.14÷2)2
=3.14×302
=3.14×900
=2826(平方米)
答:这个羊圈的面积是2826平方米。
【点评】此题主要考查圆的周长公式、面积公式的灵活运用,关键是熟记公式。
21.【答案】28.26平方厘米。
【分析】由题意可知,长方形的宽就是圆的半径,利用圆的面积公式计算即可。
【解答】解:3.14×3×3
=3.14×9
=28.26(平方厘米)
答:这个圆的面积是28.26平方厘米。
【点评】本题考查的是圆的面积公式的应用。
22.【答案】71.4米,557平方米。
【分析】(1)篱笆长,就是这个直径20米圆周长的一半加上正方形的2条边长,据此利用公式计算即可解答;
(2)菜地的面积,就是这个直径20米圆的面积一半加上正方形的面积,据此即可解答。
【解答】解:(1)20×2+3.14×20÷2
=40+31.4
=71.4(米)
(2)20×20+3.14×(20÷2)×(20÷2)÷2
=400+157
=557(平方米)
答:篱笆长71.4米,这个菜地的占地面积是557平方米。
【点评】此题主要考查正方形、圆的周长与面积的计算方法,熟记公式即可解答。
23.【答案】138.16平方米。
【分析】求小路的面积,实际上就是求圆环的面积,即用外圆的面积减内圆的面积即可;内圆的直径和外圆与内圆半径之差(即小路的宽)已知,即可分别求出内外圆的面积,问题得解。
【解答】解:小路的面积:3.14×(2+10)2﹣3.14×102
=3.14×(122﹣1002)
=3.14×(144﹣100)
=3.14×44
=138.16(平方米)
答:小路的面积是138.16平方米。
【点评】解答此题的关键是明白:求小路的面积,实际上就是求圆环的面积,即用外圆的面积减内圆的面积即可。
24.【答案】78.75平方米。
【分析】用青菜的种植面积除以青菜占总面积的百分率求出总面积,由扇形统计图可知,白菜的种植面积占总面积的90°÷360°×100%=25%,用1减去青菜和白菜占的百分率即可求出萝卜占总面积的百分率,萝卜的面积=总面积×萝卜占总面积的百分率。
【解答】解:90÷40%
=90÷0.4
=225(平方米)
90°÷360°×100%
=0.25×100%
=25%
225×(1﹣40%﹣25%)
=225×35%
=78.75(平方米)
答:王大伯家萝卜种植了78.75平方米。
【点评】解决本题关键是从图中读出数据,找出单位“1”,再根据基本的数量关系求解。
25.【答案】(1)32%;
(2)500;
(3)六十五。
【分析】(1)调查的总人数看作单位“1”,根据减法的意义,用减法解答。
(2)调查的总人数看作单位“1”,“不关心这个问题”的有25人,占调查总人数的5%,根据已知一个数的百分之几是多少,求这个数,用除法解答。
(3)把持“没影响”态度的人数看作单位“1”,先用减法求出持“影响不大”态度的人比持“没影响”态度的人多占总人数百分之几,然后根据求一个数是另一个数的百分之几,用除法解答。
【解答】解:1﹣(10%+5%+20%+33%)
=1﹣68%
=32%
答:m=32%。
(2)25÷5%
=25÷0.05
=500(人)
答:一共调查了500人。
(3)(33%﹣20%)÷20%
=0.13÷0.2
=0.65
=65%
答:持“影响不大”态度的人比持“没影响”态度的人多65%。
故答案为:32%;500;六十五。
【点评】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
26.【答案】(1)320元;
(2)720元。
【分析】(1)用200除以对应的百分率,即可求出6月份的总开支,再乘赡养老人占总开支的百分率,即可求出赡养老人支出多少元。
(2)用200除以对应的百分率,即可求出6月份的总开支,再乘食品支出占总开支的百分率,即可求出食品支出多少元。
【解答】解:(1)200÷10%×16%
=2000×16%
=320(元)
答:赡养老人支出320元。
(2)200÷10%×36%
=2000×36%
=720(元)
答:食品支出720元。
【点评】本题考查百分数的计算及应用。理解题意,找出数量关系,列式计算即可。
27.【答案】(1)800;
(2)
(3)5月20日,据官方统计,2022年5月20日当天,单日累计办理结婚登记近20万对(18个省市的数据);200台,一般购买冰箱的消费者大多为将要结婚的夫妇,5月20日这天办理结婚登记的人数比较多(答案不唯一)。
【分析】(1)把全年的销售量看作单位“1”,其中第三季度的销售量是280台,占全年销售量的35%,根据已知一个数的百分之几是多少,求这个数,用除法求出全年的销售量。
(2)把全年的销售量看作单位“1”,根据求一个数的百分之几是多少,用乘法求出第四季度的销售量,再用减法求出第二季度的销售量,据此完成统计图。
(3)促销时间定为:5月20日;选择这个时间的理由是:据官方统计,2022年5月20日当天,单日累计办理结婚登记近20万对(18个省市的数据)。备货数量:200台;预估这些数量的理由是:一般购买冰箱的消费者大多为将要结婚的夫妇,5月20日这天办理结婚登记的人数比较多(答案不唯一)。
【解答】解:(1)280÷35%
=280÷0.35
=800(台)
答:华地商场2021年一共销售冰箱800台。
(2)800×40%=240(台)
800﹣(180+280+240)
=800﹣700
=100(台)
作图如下:
(3)促销时间定为:5月20日;选择这个时间的理由是:据官方统计,2022年5月20日当天,单日累计办理结婚登记近20万对(18个省市的数据)。备货数量:200台;预估这些数量的理由是:一般购买冰箱的消费者大多为将要结婚的夫妇,5月20日这天办理结婚登记的人数比较多(答案不唯一)。
故答案为:800;5月20日,据官方统计,2022年5月20日当天,单日累计办理结婚登记近20万对(18个省市的数据);200台,一般购买冰箱的消费者大多为将要结婚的夫妇,5月20日这天办理结婚登记的人数比较多(答案不唯一)。
【点评】此题考查的目的是理解掌握条形统计图、扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
28.【答案】(1)18;
(2)3.6。
【分析】(1)混凝土的质量看作单位“1”,其中水泥占20%,水泥有3.6吨,根据已知一个数的百分之几是多少,求这个数,用除法解答。
(2)先求出河沙比石子少占混凝土质量的百分之几,再根据一个数乘百分数的意义,用乘法解答。
【解答】解:(1)3.6÷20%
=3.6÷0.2
=18(吨)
答:能配制18吨这样的混凝土。
(2)18×(50%﹣30%)
=18×0.2
=3.6(吨)
答:河沙比石子少3.6吨。
【点评】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
29.【答案】(1)10;
(2)234人;
(3)45%。
【分析】(1)把全校近视的学生人数看作单位“1”,根据减法的意义,用减法解答。
(2)根据求一个数的百分之几是多少,用乘法解答。
(3)把全校学生人数看作单位“1”,根据求一个数是另一个数的百分之几,用除法解答。
【解答】解:(1)1﹣65%﹣25%=10%
答:低年级学段学生近视人数占全校学生近视人数的10%。
(2)360×65%=234(人)
答:高年级近视学生有234人。
(3)360÷800
=0.45
=45%
答:全校学生近视率是45%。
故答案为:10。
【点评】此题考查目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
30.【答案】38。
【分析】由一张桌子坐6人,两张桌子坐10人,三张桌子坐14人,可以发现每多一张桌子多4个人,由此用字母表示这一规律,然后代值计算。
【解答】解:1张桌子可坐2×1+4=6(人)
2张桌子拼在一起可坐2×4+2=10(人)
3张桌子拼在一起可坐4×3+2=14(人)
…
所以五张桌子坐4×5+2=22(人)
…
那么n张桌子坐(4n+2)人
当n=9时,
4×9+2
=36+2
=38(人)
答:这样共9张桌子拼起来可以坐38人。
【点评】此题考查图形的变化规律,找出规律,利用规律解决问题。
31.【答案】见试题解答内容
【分析】(1)像这样拼下去,所用小正方形卡纸的张数是8、10、12……8=6+2×1、10=6+2×2、12=6+2×3……第5个图用的张数是6+2×5,第n个用的张数是6+2n.
(2)面积为1cm2的正方形边长为1cm.在第n个图形的外围用铁丝镶上一圈边框,也就求第n个图形的周长.像这样拼下去,各图形的周长分别是12、14、16……12=10+2×1、14=10+2×2、16=10+2×3……第n个图形的周长是10+2n.
【解答】解:(1)由分析可知,第(5)个图形要用多少张小正方形卡纸是:
6+2×5
=6+10
=16(张)
答:第(5)个图形要用16张小正方形卡纸.
(2)由分析可知,第n个图形的周长是10+2n
因此,如果要在第n个图形的外围用铁丝镶上一圈边框,至少需要(10+2n)厘米铁丝
答:至少需要(10+2n)厘米铁丝.
【点评】解答此题的关键是根据这些图形找出图形的序数与所用小正方形卡纸的张数、拼成图形的周长之间的关系,这也是本题的难点.
32.【答案】见试题解答内容
【分析】(1)根据图示可知,摆一个五边形需要5根小棒,摆2个五边形需要9根小棒,也可以写成5+4×1=9(根)小棒,摆3个五边形需要13根小棒,也可以写成5+4×2=13(根)小棒…以后每增加一个五边形,需要的小棒个数就会增加4根,由此可得摆n个五边形需要5+4(n﹣1)=4n+1根小棒.
(2)①根据(1)中推理的推论,摆5个五边形需要4×5+1=21根小棒,摆10个五边形需要4×10+1=41根小棒.
②根据(1)中的推理的推论,设4n+1=61,可求出n的值既是所需摆出的五边形的个数.
【解答】解:(1)根据图示可知,摆1个五边形需要5根小棒,摆2个五边形需要5+4×1=9(根)小棒,
摆3个五边形需要5+4×2=13(根)小棒.
(2)①根据(1)中推理可得:摆n个五边形需要5+4(n﹣1)=4n+1根小棒,
摆5个五边形为:4×5+1=21(根),则摆5个五边形需要21根小棒;
摆10个五边形为:4×10+1=41(根),则摆10个五边形需要41根小棒.
②当4n+1=61时,可得4n=60,最终解得:n=15,所以用61根小棒可以摆出15个五边形.
故答案为:5,9,13.
【点评】本题考查了图形变化类,解决本题的关键是观察图形找到规律,并最终进行求解.
33.【答案】
【分析】左下角、右下角以及中间这三个数的和等于最上面那个数,据此求解即可。
【解答】解:35+18+30
=53+30
=83
【点评】解答此题的关键是,根据所给出的数列的数的特点,找出规律,再根据规律解决问题。
34.【答案】180米。
【分析】根据分数与比的关系,可以把本题转化为分数问题来解答。这条水渠的全长是一个不变的量,转化过程中要把这条水渠的全长看作单位“1”。第一天修的与未修的比是2:7,也就是第一天修的占全长的22+7。再修50米,此时修完的占全长的12。说明50米相当于单位“1”的(12−22+7)。单位“1”的量未知,根据已知量÷已知量占单位“1”的几分之几=单位“1”的量,可以求出这条水渠的总长度。
【解答】解:50÷(12−22+7)
=50÷(12−29)
=50÷(918−418)
=50÷518
=50×185
=180(米)
答:这条水渠长180米。
【点评】在把关于比的问题转化为分数问题时,通常把题中不变量看作单位“1”。
35.【答案】400个。
【分析】把这批零件的个数看作单位“1”,已知师傅和徒弟每小时加工零件个数的比是8:5,当师傅完成任务时,徒弟还有75个没有完成,也就是徒弟已经加工的个数是师傅加工个数的58,那么75个相当于师傅加工个数的(1−58),根据已知一个数的几分之几是多少,求这个数,用除法求出师傅加工了多少个,然后乘2即可求出这批零件一共有多少个。
【解答】解:75÷(1−58)×2
=75÷38×2
=75×83×2
=200×2
=400(个)
答:这批零件一共有400个。
【点评】此题解答关键是确定单位“1”,重点的求出75个占师傅加工数量的几分之几,然后根据已知一个数的几分之几是多少,求这个数,用除法解答。
36.【答案】(1)3:2;(2)12分;(3)72根。
【分析】(1)把挂彩带的工作量看作“1”,用“工作量÷工作时间=工作效“的关系式,求出各自的工作效率,写出比并化简即可;
(2)用工作量除以他俩的工作效率的和,即可解答;
(3)根据题意可得,小月挂的彩带数量×(1−13)=小玉挂的彩带数量,据此关系式求出小玉挂的彩带数量,小月、小玉挂的彩带根数和16根一共是7份,求出1份几根,要挂的彩带是7+2=9(份),据此解答所求问题。
【解答】解:(1)1÷20=120
1÷30=130
120:130=3:2
答:小月和小玉的工作效率的比是3:2。
(2)1÷(120+130)
=1÷112
=12(分)
答:如果两人同时挂彩带,一共需要12分钟才能完成任务。
(3)24×(1−13)
=24×23
=16(根)
24+16+16=56(根)
56÷7×(7+2)
=8×9
=72(根)
答:六(6)教室一共要挂72根彩带。
故答案为:3:2
【点评】本题考查的是比的应用,灵活掌握工作量、工作效率和工作时间这三个数量之间的关系,根据比找到各数量所占的份数是解答的关键。
37.【答案】7500千克;17500千克。
【分析】根据题意,原来的两个仓库面粉和等于现在的两个仓库的面粉和,原来的甲仓库面粉是甲乙两仓库面粉和的33+7=310,现在的甲仓库面粉是甲乙两仓库面粉和的22+3=25,2500千克是甲乙两仓库面粉和的(25−310),据此列出数量关系式,求出甲乙两个仓库的面粉综合,再根据原来的甲乙两仓库的面粉比,按比分配,进而列式解答。
【解答】解:3+7=10
2500÷(25−310)
=2500÷110
=25000(千克)
25000÷(3+7)
=2500(千克)
2500×3=7500(千克)
2500×7=17500(千克)
答:甲仓库原来有7500千克面粉,乙仓库原来有17500千克面粉。
【点评】本题考查的是比的应用,找不变量为标准作单位“1”,分别算出比较量变化前与变化后各占标准量的几分之几,算出已知数量的对应分率,进而求出标准量,再按比分配求得各自的数量。
38.【答案】香蕉100千克,苹果120千克,梨50千克。
【分析】依据题意可设香蕉是5x千克,则苹果是6x千克,梨是(12×6x﹣10)千克,利用香蕉、苹果和梨一共270千克,列方程计算运来的香蕉、苹果和梨各有多少千克。
【解答】解:设香蕉是5x千克,则苹果是6x千克,梨是(12×6x﹣10)千克,由题意得:
12×6x﹣10+5x+6x=270
3x﹣10+5x+6x=270
14x=280
x=20
5×20=100(千克)
6×20=120(千克)
270﹣100﹣120=50(千克)
答:香蕉100千克,苹果120千克,梨50千克。
【点评】本题考查的是比的应用。
39.【答案】(1)69,(2)960万平方千米。
【分析】(1)把山地、丘陵和高原的地区占到全国陆地面积的分率相加即可解答;
(2)求我国陆地领土面积,根据已知一个数的几分之几是多少,求这个数,用我国平原的面积除以我国平原的面积占全国陆地面积的分率即可解答。
【解答】解:(1)33%+10%+26%
=43%+26%
=69%
答:我国山区的面积占到全国陆地面积的69%。
(2)115.2÷12%=960(万平方千米)
答:我国陆地领土面积约960万平方千米。
故答案为:69。
【点评】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
(期末押题卷)广东省广州市2023-2024学年六年级上学期数学高频易错期末预测必刷卷(人教版): 这是一份(期末押题卷)广东省广州市2023-2024学年六年级上学期数学高频易错期末预测必刷卷(人教版),共17页。试卷主要包含了选择题,填空题,判断题,计算题,作图题,解答题等内容,欢迎下载使用。
(期末押题卷)广东省2023-2024学年六年级上学期数学高频易错期末预测必刷卷(人教版): 这是一份(期末押题卷)广东省2023-2024学年六年级上学期数学高频易错期末预测必刷卷(人教版),共17页。试卷主要包含了选择题,填空题,判断题,计算题,作图题,解答题等内容,欢迎下载使用。
(期末押题卷)期末解决问题-重庆市2023-2024学年六年级上学期数学高频易错期末预测必刷卷(人教版): 这是一份(期末押题卷)期末解决问题-重庆市2023-2024学年六年级上学期数学高频易错期末预测必刷卷(人教版),共21页。试卷主要包含了根据如图说说冬冬上学的路线,路线图,植树队要种200棵数等内容,欢迎下载使用。













