安徽省马鞍山市第二中学2022-2023学年高二下学期期中考试数学试卷(含答案)

这是一份安徽省马鞍山市第二中学2022-2023学年高二下学期期中考试数学试卷(含答案)，共13页。试卷主要包含了选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。


一、选择题
1、从1,2,3,4,5这5个数中任取3个不同的数,可组成不同的等差数列的个数为( )
A.2B.4C.6D.8
2、若,则( )
A.2B.1C.D.
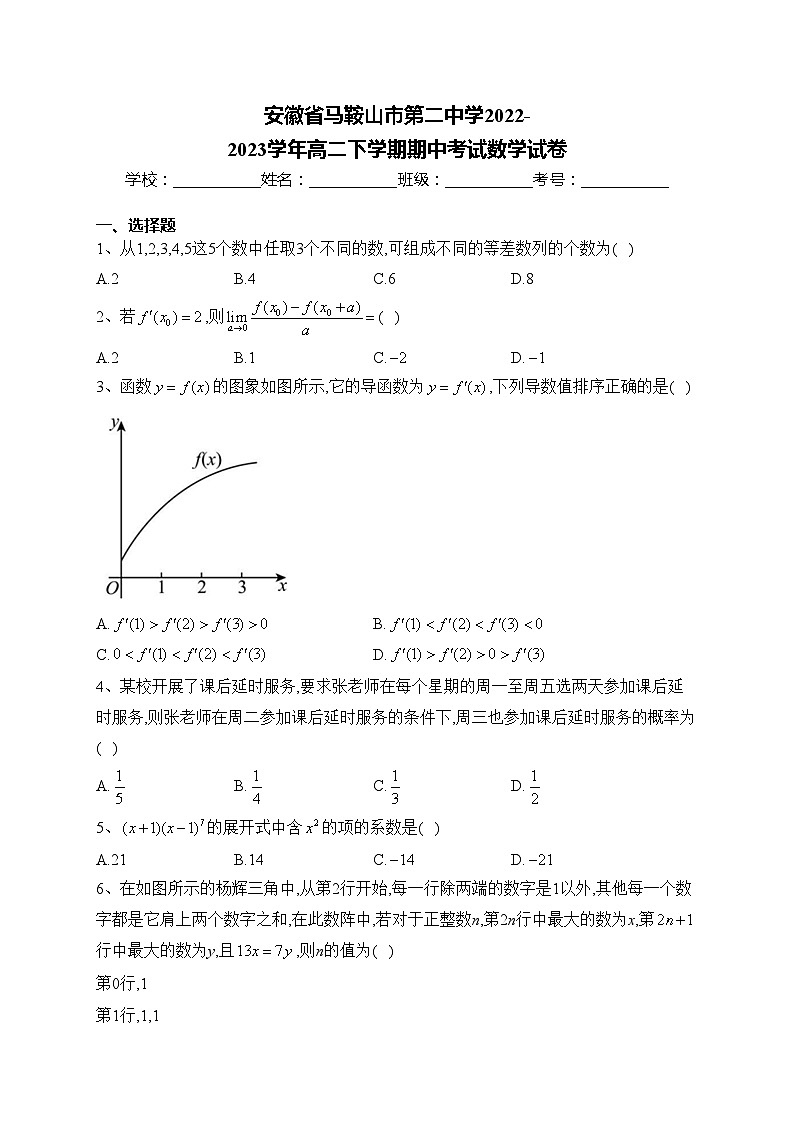
3、函数的图象如图所示,它的导函数为,下列导数值排序正确的是( )
A.B.
C.D.
4、某校开展了课后延时服务,要求张老师在每个星期的周一至周五选两天参加课后延时服务,则张老师在周二参加课后延时服务的条件下,周三也参加课后延时服务的概率为( )
A.B.C.D.
5、的展开式中含的项的系数是( )
A.21B.14C.D.
6、在如图所示的杨辉三角中,从第2行开始,每一行除两端的数字是1以外,其他每一个数字都是它肩上两个数字之和,在此数阵中,若对于正整数n,第2n行中最大的数为x,第行中最大的数为y,且,则n的值为( )
第0行,1
第1行,1,1
第2行,1,2,1
第3行,1,3,3,1
第4行,1,4,6,4,1
第5行,1,5,10,10,5,1
第6行,1,6,15,20,15,6,1
A.5B.6Ｃ.7Ｄ.8
7、已知数列的前n项和为,,,则( )
A.675B.674C.1384D.2023
8、若存在,使得不等式成立,则实数m的最大值为( )
A.4B.C.D.
二、多项选择题
9、已知A,B是两个随机事件,,则下列说法正确的是( )
A.若A,B相互独立,则B.若事件,则
C.若A,B是对立事件,则D.若A,B是互斥事件,则
10、已知在等比数列中,,公比,则( )
A.数列是等比数列B.数列是等差数列
C.数列是等比数列D.数列是等差数列
11、已知的展开式的第5项与第7项的二项式系数相等,且展开式的各项系数之和为1024,则下列说法正确的是( )
A.展开式中奇数项的二项式系数之和为256
B.展开式中第6项的系数最大
C.展开式中存在常数项
D.展开式中含的项的系数为45
12、已知,且,其中e为自然对数的底数,则下列选项中正确的是( )
A.B.C.D.
三、填空题
13、某学生参与一种答题游戏,需要从A,B,C三道试题中选出一道进行回答,回答正确即可获得次品.若该学生选择A,B,C的概率分别为0.3,0.4,0.3,答对A,B,C的概率分别为0.4,0.5,0.6,则其获得奖品的概率为________.
14、已知数列为等比数列,是其前n项和,若,,则________.
15、2023年春节期间,电影院上映《流浪地球2》《潢江红》《熊出没伴我“熊芯”》等多部电影,某居委会有6张不同的电影票,奖励给甲,乙,丙三户“五好文明家庭”,其中一户1张,一户2张,一户3张,则共有________种不同的分法.
16、已知函数,,,则mn的最小值是________.
四、解答题
17、已知数列中,,.
（1）求证:是等比数列;
（2）若数列满足,求数列的前n项和.
18、（1）3名男生和4名女生站成一排,男生站在一起,女生站在一起,有多少种不同的排队方法?
（2）3名男生和4名女生站成一排,男生彼此不相邻,有多少种不同的排队方法?
（3）把6个人平均分成3个小组,有多少种不同的分法?
19、周末李梦提出和父亲,母亲,弟弟进行羽毛球比赛,李梦与他们三人各进行一场比赛,共进行三场比赛,而且三场比赛相互独立.根据李梦最近分别与你父亲,母亲,弟弟比赛的情况,得到如下统计表:
以上表中的频率作为概率,求解下列问题:
（1）若李梦胜一场得1分,负一场得0分,设李梦的得分为X,求X的分布列,期望和方差;
（2）如果李梦赢一场比赛能得到5元的奖励资金,请问李梦所得资金的期望和方差.
20、已知函数,且满足的导数的最小值为.
（1）求a的值;
（2）若函数在区间上的最大值与最小值的和为7,求b的值.
21、已知函数.
（1）当时,求的单调区间与极值;
（2）当时,证明:只有一个零点.
22、证明:当时,.
参考答案
1、答案：D
解析：按公差正负可分两类:第一类,公差大于0,有1,2,3;2,3,4;1,3,5;3,4,5,共4个等差数列;第二类,公差小于0,有3,2,1;4,3,2;5,3,1;5,4,3,共4个等差数列,根据加法原理,共可组成个不同的等差数列.
故选D.
2、答案：C
解析：根据导数的定义,得.
故选C.
3、答案：A
解析：由图象可知,函数在上单调递增,所以当时,,即
,,,又因为曲线在点处切线的斜率随着x的增大而减小,即导函数单调递减,故.
故选A.
4、答案：B
解析：记事件A表示“张老师在周二参加课后延时服务”,事件B表示“张老师在周三参加课后延时服务”,则,,所以.
故选B.
5、答案：C
解析：因为展开式的通项为,所以展开式中含的项的系数为,
故选C.
6、答案：B
解析：由题意知,,,故,即,
,,解得.
故选B.
7、答案：A
解析：
.
故选A.
8、答案：D
解析：若存在,使得不等式成立,等价于存在,使得不等式成立,设,则.
因为,当时,,当时,,
所以在上单调递减,在上单调递增,又,,
且,所以.
故选D.
9、答案：ABD
解析：对于A,若随机事件A,B相互独立,则,所以,
A正确;
对于B,若事件,则,,B正确;
对于C,因为A,B是对立事件,所以,所以,所以C不正确;对于D,因为A,B是互斥事件,所以,所以,D正确.
故选ABD.
10、答案：CD
解析：在等比数列中,,公比,故.
对于A,,
数列是由0构成的常数列,不是等比数列,故A错误;
对于B,,故数列是等比数列,B错误;
对于C,,所以数列是等比数列,C正确;
对于D,,所以数列是等差数列,D正确.
故选CD.
11、答案：BCD
解析：由二项式的展开式的第5项与第7项的二项式系数相等可知,所以,又展开式的各项系数之和为1014,即当时,,可得,所以二项式为,则展开式中奇数项的二项式系数之和为,故A错误;
由可知展开式共有11项,中间项的二项式系数最大,即第6项的二项式系数最大,因为与的系数均为1,所以该二项展开式的系数与二项式系数相同,所以展开式中第6项的系数最大,故B正确;的展开式的通项为,令,解得,即展开式中存在常数项,故C正确;令,解得,所以展开式中含的项的系数为,故D正确.
故选BCD.
12、答案：BC
解析：因为,所以,令,,
则,由,得,
由,得,所以在单调递增,在上单调递减,
因为,由有:,故A错误.
因为,所以,由得,,故D错误;
因为,所以,,
因为,所以,所以,故C正确;
令,
则,当时,恒成立,所以在单调递增,由得,,所以,即,又,所以,因为,
所以,因为在内单调递减,所以,即,故B正确.故选BC.
13、答案：0.5
解析：该学生获得奖品的概率为.
14、答案：12
解析：设等比数列的公比为q,,由得,因为,所以,
由,得,所以.
15、答案：360
解析：从6张电影票中任选1张,有种选法,从余下的5张中任选2张有种选法,最后余下3张选3张有种选法,由于甲,乙,丙是不同的三户“五好文明家庭”,因此共有种不同的分法.
16、答案：
解析：由函数,,,得,所以,,
令,,则,当时,,当时,,所以函数在上单调递减,在上单调递增,所以的最小值为,
即mn的最小值为.
17、答案：（1）见解析
（2）见解析
解析：（1）证明:因为,所以,
又 ,所以,所以是以1为首项,2为公比的等比数列.
（2）由（1）知,则,
,
,
两式相减,得,所以.
18、答案：（1）288
（2）1440
（3）15
解析：（1）男生全排列的排法有种,再把女生看成一个整体,女生全排列有种,再把这两个整体全排列,共有(种)排法;
（2）先排女生,有种排法,排好后有5个空位,让男生插入5个空位中,有种排法,故共有(种)排法;
（3）有(种)不同的分法.
19、答案：（1）见解析
（2）见解析
解析：（1）李梦与爸爸比赛获胜的概率为;与妈妈比赛获胜的概率为;
与弟弟比赛获胜的概率为;
X的可能取值为0,1,2,3.
则;
;
;
.
故分布列为:
,;
（2）,.
20、答案：（1）
（2）
解析：（1）,则的最小值为,
由题意可得:.
（2）由（1）可得,,则,
由,解得或;由,解得;
所以在上单调递增,在上单调递减,在上单调递增,
又,,,,
且,
所以函数在区间上的最大值为,最小值为.
又因为函数在区间上的最大值与最小值的和为7,
所以,解得.
21、答案：（1）见解析
（2）见解析
解析：（1）当时,,,
则,
当时,,当时,,
所以在上单调递增,在上单调递减,
所以在处取得极大值,无极小值.
（2）因为,
所以,
①当时,,在上单调递增,
因为,,即,
所以在上有唯一零点;
②当时,由,得或,且,
由,解得或,由,解得,
所以在上单调递增,在上单调递减,在上单调递增,
又,,
所以,故上有唯一零点,
综上,当时,只有一个零点.
22、答案：（1）见解析
（2）见解析
解析：（1）证明:当时,,
不等式等价于,
令,,
则,
因为当时,,所以,
于是.
所以在上单调递增,所以.
（2）当时,,,所以.
综上,当时,即成立.
父亲
母亲
弟弟
比赛次数
50
60
40
李梦获胜次数
10
30
32
X
0
1
2
3
P