河南省驻马店市平舆县2023-2024学年九年级上学期12月月考数学模拟试题（含答案）

这是一份河南省驻马店市平舆县2023-2024学年九年级上学期12月月考数学模拟试题（含答案），共10页。

注意事项：
1．本试卷共6页，三个大题，满分120分，考试时间100分钟。
2．答卷前请将装订线内的项目填写清楚。
一、选择题（每小题3分，共30分）下列各小题均有四个选项，其中只有一个是正确的，将正确答案的代号字母填在题后括号内．
1．2023年11月，河南智慧交通产业博览会举办，旨在助推交通产业高质量发展，谋划新时代智慧交通新格局．下列“智慧交通”的首字母中，是中心对称图形的共有（）
A．1个B．2个C．3个D．4个
2．下列不能由抛物线平移得到的是（）
A．B．C．D．
3．如图，四边形是的内接四边形，，则（）
A．B．C．D．
4．某淘宝商家为“双11大促”提前进行了预热抽奖，通过后台的数据显示转盘指针落在“10元优惠券”区域的统计数据如下表．若随机转动转盘一次，得到“10元优惠券”的概率为（精确到0.01）（）
A．0.32B．0.31C．0.30D．0.29
5．如图，点是的外接圆的圆心，若，则（）
A．B．C．D．
6．如图，点为反比例函数的图象上一点，过点作轴．垂足为．若的面积为4，则的值为（）
A．4B．C．8D．
7．如图，与是位似图形，点为位似中心，已知，则（）
A．B．C．2:1D．
8．如图，直线，直线和被所截，，则的长为（）
A．0.4B．1.4C．2D．2.4
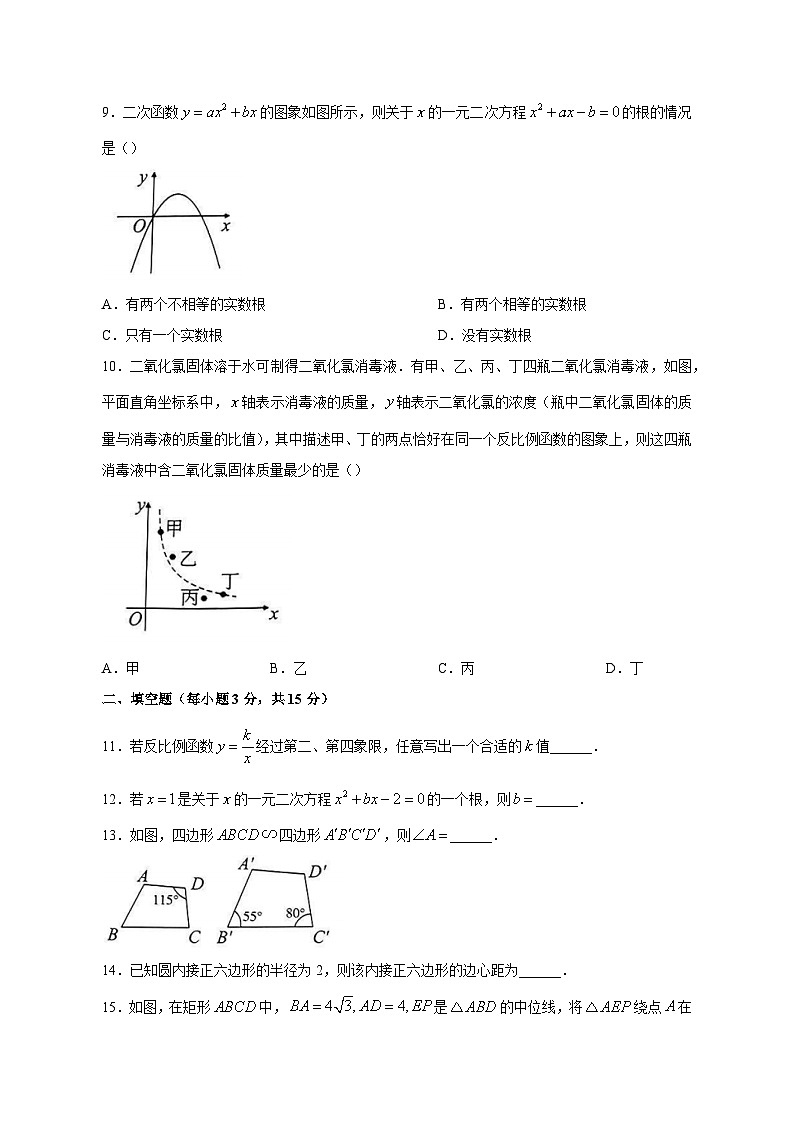
9．二次函数的图象如图所示，则关于的一元二次方程的根的情况是（）
A．有两个不相等的实数根B．有两个相等的实数根
C．只有一个实数根D．没有实数根
10．二氧化氯固体溶于水可制得二氧化氯消毒液．有甲、乙、丙、丁四瓶二氧化氯消毒液，如图，平面直角坐标系中，轴表示消毒液的质量，轴表示二氧化氯的浓度（瓶中二氧化氯固体的质量与消毒液的质量的比值），其中描述甲、丁的两点恰好在同一个反比例函数的图象上，则这四瓶消毒液中含二氧化氯固体质量最少的是（）
A．甲B．乙C．丙D．丁
二、填空题（每小题3分，共15分）
11．若反比例函数经过第二、第四象限，任意写出一个合适的值______．
12．若是关于的一元二次方程的一个根，则______．
13．如图，四边形四边形，则______．
14．已知圆内接正六边形的半径为2，则该内接正六边形的边心距为______．
15．如图，在矩形中，是的中位线，将绕点在平面内自由旋转，当三点在同一条直线上时，的长为______．
三、解答题（本大题共8个小题，共75分）
16．（10分）解方程:（1）；（2）．
17．（9分）某外企公司招聘员工，考核内容有三项，包括基础知识测验、专业知识测验和外语能力测验．其中，专业知识测验为必测科目，基础知识测验可从“企业管理常识”和“计算机操作”中二选一，外语能力测验可从“英语口语”和“书面翻译”中二选一．
（1）针对每一名应聘人员共有______种选择方案；
（2）请用画树状图或列表的方法，求同时来应聘的嘉嘉与淇淇选择同一种方案的概率．
18．（9分）郑州二七纪念塔作为郑州的城市地标，坐落在距离郑州火车站不远的二七广场，共14层，为仿古联体双塔，是中国最年轻的全国重点文物保护单位．郑州某初中数学兴趣小组为测量其高度，设计了如下方案，请据此求出二七纪念塔高度．
19．（9分）已知二次函数．
（1）求出该二次函数的对称轴；
（2）在所给的坐标系中画出这个函数的大致图象；（直接画图即可）
（3）当时，求的取值范围．
20．（9分）如图，在平面直角坐标系中，直线经过原点，且与反比例函数交于点、点，分别以为圆心，1为半径作和，分别切轴于两点．
（1）求反比例函数的解析式；
（2）填空：①当时，的取值范围是______；
②图中阴影部分的面积是______（结果保留）．
21．（9分）如图，为的直径，过圆外一点作切线交于点和点，
连接和．
（1）求证：；
（2）填空：①当______时，四边形为菱形；
②当______时，四边形为正方形．
22．（10分）如图，在平面直角坐标系中，点在轴上，球网与轴的水平距离，
球网高度，击球点在轴上，且．吊球时羽毛球的飞行高度
与水平距离满足二次函数关系．
（1）羽毛球离地的最大高度为______m；
（2）求；
（3）通过计算说明羽毛球能否过网，并计算落地点到球网的距离．
23．（10分）综合与实践
综合与实践课上，老师让同学们以“正方形的折叠”为主题开展数学活动．
（1）操作猜想
操作一：如图1，对折正方形纸片，使与重合，得到折痕，把纸片展平；
操作二：如图2，继续沿折叠，使点落在正方形内部点处，把纸片展平，连接、；
根据以上操作，在图2中，写出一个与相等的角______．
（2）探究证明
①如图3，延长交于点，连接，则与的大小关系是______；线段之间的数量关系是______；
②判断点在上的位置，并说明理由．
（3）拓展延伸
如图4，若正方形的边长为，直接写出点到线段的距离．
九年级数学答案
1－5BDCCC6－10DACAC11．（不唯一）12．113．11014．
15．或
16．解:（1）原方程的解是；（2）原方程的解是．
17．解:（1）4；参考：每名应聘人员可选择：专业知识测验、企业管理常识、英语口语（用表示）；专业知识测验、计算机操作、书面翻译（用表示）；专业知识测验、企业管理常识、书面翻译（用表示）；专业知识测验、计算机操作、英语口语（用表示）．共有4种选择方案．故4
（2）用代表四种选择方案
用列表法分析如下：
两人选择的方案共有16种等可能的结果，其中选择同种方案的结果有4种，所以嘉嘉与淇淇选择同种方案的概率．
18．解：由题意得，，
，将数据代入，解得．
19．解：（1）对称轴为
（2）如右图．
（3）根据函数图象可知：当时，有最大值：4，当时，，故的取值范围是．
20．解:（1）反比例函数过点、点，
解得：反比例函数的解析式为：；
（2）①或②
21．解:（1）证明：为的切线，，
，又，
；
（2）①30②45
22．解:（1）3.2；
（2）将代入，可解得：；
（3）当时，，故羽毛球能过网；
另，即，解得：或（舍去）
故落地点到球网的距离是：
23．解：（1）（不唯一）
（2）①
②点是线段的三等分点且靠近点的位置。（注：若没有写出判断结果，但后续理由正确，不扣分）
理由：四边形是正方形，，
由翻折的性质可知，，
RtRt，
，
设正方形纸片的边长为，则，设，则
在Rt中，根据勾股定理可知:，
解得点是线段的三等分点且靠近点的位置
（3）转动转盘的次数
200
600
1000
1600
2000
落在“10元优惠券”区域的次数
64
186
300
472
602
落在“10元优惠券”区域的频率
0.320
0.310
0.300
0.295
0.301
主题
测量二七纪念塔高度
工具
测角仪、皮尺等
人员
组长:；组员:
实物及
示意图
方案
说明
1．．
2．点在一条水平线上．
3．平面镜的大小和厚度忽略不计．
组员在点处放置一个平面镜，站在处恰好
能从平面镜中看到塔的顶端，分别测出：
组员到平面镜距离、
平面镜到塔底部中心的距离
组员眼睛到地面距离．
数据
评价
嘉嘉
淇淇