2022-2023学年河南省南阳市卧龙区新时代精英学校八年级（上）期末数学试卷（含解析）

这是一份2022-2023学年河南省南阳市卧龙区新时代精英学校八年级（上）期末数学试卷（含解析），共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.在实数：3.14159，364，1.010 010001， 7，π，27中，无理数有( )
A. 1个B. 2个C. 3个D. 4个
2.已知图中的两个三角形全等，则∠α等于( )
A. 72°B. 60°C. 58°D. 50°
3.如图，在△ABC中，AB的垂直平分线分别交AB、BC于点D、E，连接AE，若AE=4，EC=2，则BC的长是( )
A. 8
B. 6
C. 4
D. 2
4.3的算术平方根是( )
A. 9B. −9C. 3D. ± 3
5.我们经常将调查、收集得来的数据用各类统计图进行整理与表示．下列统计图中，能凸显由数据所表现出来的部分与整体的关系的是( )
A. 条形图B. 扇形图C. 折线图D. 频数分布直方图
6.如图．△ABC中，∠ACB=90°，将△ABC绕点C顺时针旋转得到△EDC，使点B的对应点D恰好落在AB边上，AC、ED交于点F.若∠BCD=α，则∠EFC的度数是(用含α的代数式表示)( )
A. 90°+12αB. 90°−12αC. 180°−32αD. 32α
7.如图，在△ABC中，分别以点B和点C为圆心，大于12BC长为半径画弧，两弧相交于点M，N.作直线MN，交AC于点D，交BC于点E，连接BD.若AB=7，AC=12，BC=6，则△ABD的周长为( )
A. 25B. 22C. 19D. 18
8.观察下列作图痕迹，所作线段CD为△ABC的角平分线的是( )
A. B.
C. D.
9.如图，已知△ABC中，∠CAB=20°，∠ABC=30°，将△ABC绕A点逆时针旋转50°得到△AB′C′，以下结论：①BC=B′C，②AC//C′B′，③C′B′⊥BB′，④∠ABB′=∠ACC′，正确的有( )
A. ①②③
B. ①②④
C. ①③④
D. ②③④
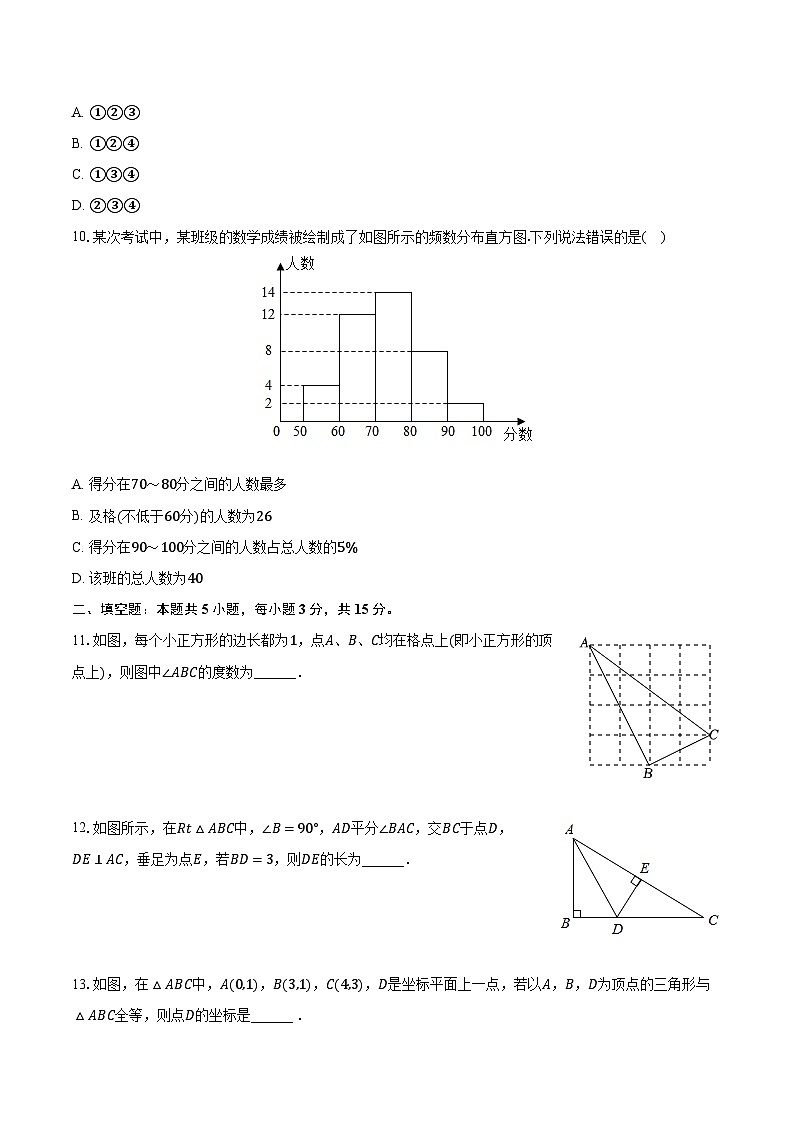
10.某次考试中，某班级的数学成绩被绘制成了如图所示的频数分布直方图.下列说法错误的是( )
A. 得分在70～80分之间的人数最多
B. 及格(不低于60分)的人数为26
C. 得分在90～100分之间的人数占总人数的5%
D. 该班的总人数为40
二、填空题：本题共5小题，每小题3分，共15分。
11.如图，每个小正方形的边长都为1，点A、B、C均在格点上(即小正方形的顶点上)，则图中∠ABC的度数为______．
12.如图所示，在Rt△ABC中，∠B=90°，AD平分∠BAC，交BC于点D，DE⊥AC，垂足为点E，若BD=3，则DE的长为______．
13.如图，在△ABC中，A(0,1)，B(3,1)，C(4,3)，D是坐标平面上一点，若以A，B，D为顶点的三角形与△ABC全等，则点D的坐标是______ ．
14.如图，已知在△ABD和△ABC中，∠DAB=∠CAB，点A、B、E在同一条直线上，若使△ABD≌△ABC，则还需添加的一个条件是 .(只填一个即可)
15.如图，△ABC的边CB关于CA的对称线段是CB′，边CA关于CB的对称线段是CA′，连结BB′，若点A′落在BB′所在的直线上，∠ABB′=56°，则∠ACB=______度．
三、解答题：本题共8小题，共75分。解答应写出文字说明，证明过程或演算步骤。
16.(本小题8分)
先化简，再求值：(x+1)2+(2+x)(2−x)，其中x=1．
17.(本小题8分)
如图，B是线段AC的中点，AD/​/BE，BD//CE.求证：△ABD≌△BCE．
18.(本小题8分)
先化简，再求值：2(x−2y)2−(2y+x)(−2y+x)，其中x=−1，y=−2．
19.(本小题8分)
已知：如图，△ABC中，∠ABC=70°，点D，E分别在AB，AC上，BD=BC，连接BE，将线段BE绕点B按逆时针方向旋转70°得到线段BF，连接DF．
求证：△BCE≌△BDF．
20.(本小题9分)
如图，已知AB=AD，AE=AC，∠DAB=∠EAC.求证：△ACD≌△AEB．
21.(本小题9分)
长清的园博园广场视野开阔，阻挡物少，成为不少市民放风筝的最佳场所，某校七年级(1)班的小明和小亮学习了“勾股定理”之后，为了测得风筝的垂直高度CE，他们进行了如下操作：①测得水平距离BD的长为15米；②根据手中剩余线的长度计算出风筝线BC的长为25米；③牵线放风筝的小明的身高为1.6米．
(1)求风筝的垂直高度CE；
(2)如果小明想风筝沿CD方向下降12米，则他应该往回收线多少米？
22.(本小题12分)
对于结论：当a+b=0时.a3+b3=0也成立.若将a看成a3的立方根，b看成b3的立方根.由此得出结论：“如果两数的立方根互为相反数，那么这两个数也互为相反数”
(1)举一个具体的例子进行验证；
(2)若37−y和32y−5互为相反数，且x−3的平方根是它本身，求x+y的立方根．
23.(本小题13分)
已知：如图，AB/​/CD，∠ABD=90°，∠AED=90°，BD=DE.求证：∠AFC=2∠ADC．
答案和解析
1.【答案】B
【解析】解：364=4，
无理数有 7，π，共有2个，
故选：B．
根据无理数的意义判断即可．
本题考查了无理数，算术平方根，立方根，掌握无限不循环小数是无理数是解题的关键，注意0.1010010001是有限小数，属于有理数．
2.【答案】D
【解析】解：∵图中的两个三角形全等，
∴∠α=50°．
故选：D．
直接利用全等三角形的性质得出对应角进而得出答案．
本题主要考查了全等三角形的性质，正确找出对应角是解题关键．
3.【答案】B
【解析】解：∵DE是AB的垂直平分线，
∴BE=AE=4，
∴BC=BE+EC=4+2=6，
故选：B．
根据线段的垂直平分线的性质得到BE=AE=4，结合图形计算即可．
本题考查的是线段的垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．
4.【答案】C
【解析】解：3的算术平方根是 3．
故选：C．
如果一个正数x的平方等于a，即x2=a，那么这个正数x叫做a的算术平方根．记为 a，由此即可得到答案．
本题考查算术平方根，关键是掌握算术平方根的定义．
5.【答案】B
【解析】解：统计图中，能凸显由数据所表现出来的部分与整体的关系的是扇形图，
故选：B．
根据统计图的特点判定即可．
本题考查了统计图的选择，熟练掌握各统计图的特点是解题的关键．
6.【答案】C
【解析】解：由旋转的性质可知，BC=CD，∠B=∠EDC，∠A=∠E，∠ACE=∠BCD，
∵∠BCD=α，
∴∠B=∠BDC=180°−α2=90°−α2，∠ACE=α，
∵∠ACB=90°，
∴∠A=90°−∠B=α2．
∴∠E=α2．
∴∠EFC=180°−∠ECF−∠E=180°−32α.
故选：C．
由旋转的性质可知，BC=CD，∠B=∠EDC，∠A=∠E，∠ACE=∠BCD，因为∠BCD=α，所以∠B=∠BDC=180°−α2=90°−α2，∠ACE=α，由三角形内角和可得，∠A=90°−∠B=α2.所以∠E=α2.再由三角形内角和定理可知，∠EFC=180°−∠ECF−∠E=180°−32α.
本题主要考查旋转的性质，三角形内角和等相关内容，由旋转的性质得出∠E和∠ECF的角度是解题关键．
7.【答案】C
【解析】解：由题意可得，
MN垂直平分BC，
∴DB=DC，
∵△ABD的周长是AB+BD+AD，
∴AB+BD+AD=AB+DC+AD=AB+AC，
∵AB=7，AC=12，
∴AB+AC=19，
∴△ABD的周长是19，
故选：C．
根据题意可知MN垂直平分BC，可得到DB=DC，然后得到AB+BD+AD=AB+DC+AD=AB+AC，从而可以求得△ABD的周长．
本题考查线段垂直平分线的性质，三角形的周长，解答本题的关键是明确题意，利用数形结合的思想解答．
8.【答案】C
【解析】解：根据基本作图，A、D选项中为过C点作AB的垂线，B选项作AB的垂直平分线得到AB边上的中线CD，C选项作CD平分∠ACB．
故选：C．
根据基本作图的方法对各选项进行判断．
本题考查了作图−基本作图：熟练掌握基本作图(作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线).也考查了三角形的角平分线、中线和高．
9.【答案】B
【解析】解：①∵△ABC绕A点逆时针旋转50°得到△AB′C′，
∴BC=B′C′，故①正确；
②∵△ABC绕A点逆时针旋转50°，
∴∠BAB′=50°．
∵∠CAB=20°，
∴∠B′AC=∠BAB′−∠CAB=30°．
∵∠AB′C′=∠ABC=30°，
∴∠AB′C′=∠B′AC．
∴AC//C′B′，故②正确；
③在△BAB′中，
AB=AB′，∠BAB′=50°，
∴∠AB′B=∠ABB′=12(180°−50°)=65°．
∴∠BB′C′=∠AB′B+∠AB′C′=65°+30°=95°．
∴C′B′与BB′不垂直，故③不正确；
④在△ACC′中，
AC=AC′，∠CAC′=50°，
∴∠ACC′=12(180°−50°)=65°．
∴∠ABB′=∠ACC′，故④正确．
∴①②④这三个结论正确．
故选：B．
根据旋转的性质可得，BC=B′C′∠C′AB′=∠CAB=20°，∠AB′C′=∠ABC=30°，再根据旋转角的度数为50°，通过推理证明对①②③④四个结论进行判断即可．
本题考查了旋转性质的应用，图形的旋转只改变图形的位置，不改变图形的形状与大小．
10.【答案】B
【解析】解：A.得分在70～80分之间的人数最多，有14人，此选项正确，不符合题意；
B.及格(不低于60分)的人数为12+14+8+2=36(人)，此选项错误，符合题意；
C.∵总人数为4+12+14+8+2=40(人)，
∴得分在90～100分之间的人数占总人数的百分比为240×100%=5%，此选项正确，不符合题意；
D.该班的总人数为40，此选项正确，不符合题意；
故选：B．
根据频数分布直方图得出各分数段内的人数，再据此对各选项逐一判断即可．
本题考查频数分布直方图，解题的关键是读懂图象信息，属于中考常考题型．
11.【答案】90°
【解析】解：由题意得：
AB2=22+42=20，
CB2=22+12=5，
AC2=32+42=25，
∴AB2+BC2=AC2，
∴△ABC是直角三角形，
∴∠ABC=90°，
故答案为：90°．
先利用勾股定理求出AB2，BC2，AC2，再利用勾股定理的逆定理证明△ABC是直角三角形，即可解答．
本题考查了勾股定理的逆定理，勾股定理，熟练掌握勾股定理的逆定理，以及勾股定理是解题的关键．
12.【答案】3
【解析】解：∵AD平分∠BAC交BC于点D，DE⊥AC，DB⊥AB，
∴DE=DB=3．
故答案为：3．
直接根据角平分线的性质求解．
本题考查了角平分线的性质：角的平分线上的点到角的两边的距离相等．
13.【答案】(−1,3)或(−1,−1)或(4,−1)
【解析】解：如图，满足条件的点D有三个，D(−1,3)，D′(−1,−1)，D″(4,−1)．
故答案为：(−1,3)或(−1,−1)或(4,−1)．
根据对称性画出图形可得结论．
本题考查全等三角形的性质，坐标与图形性质等知识，解题的关键是正确画出图形解决问题．
14.【答案】AD=AC(答案不唯一)
【解析】【分析】
利用全等三角形的判定方法添加条件．
本题考查了全等三角形的判定：熟练掌握全等三角形的5种判定方法，选用哪一种方法，取决于题目中的已知条件．
【解答】
解：∵∠DAB=∠CAB，AB=AB，
∴当添加AD=AC时，可根据“SAS”判断△ABD≌△ABC；
当添加∠D=∠C时，可根据“AAS”判断△ABD≌△ABC；
当添加∠ABD=∠ABC时，可根据“ASA”判断△ABD≌△ABC．
当添加∠DBE=∠CBE时，可根据“ASA”判断△ABD≌△ABC．
故答案为AD=AC(答案不唯一)．
15.【答案】28
【解析】解：连接BA′，AC与BB′交点为O，如图：
∵CB关于CA的对称线段是CB′，
∴BB′⊥AC，
∵∠ABB′=56°，
∴∠BAC=34°，
∵边CA关于CB的对称线段是CA′，
∴△A′CB≌△ACB，
∴∠BA′C=∠BAC=34°，
∴∠ACA′=2∠ACB=56°，
∴∠ACB=28°．
根据对称性可判断出BB′⊥AC，先求出∠BAC=34°，再根据对称的性质判断△A′CB≌△ACB，最后根据∠ACA′=2∠ACB即可求解．
本题主要考查轴对称的性质，及三角形全等的判定及性质，熟练掌握轴对称的性质是解答本题的关键．
16.【答案】解：(x+1)2+(2+x)(2−x)
=x2+2x+1+4−x2
=2x+5，
当x=1时，原式=2+5=7．
【解析】先根据完全平方公式和平方差公式进行计算，再合并同类项，最后代入求出答案即可．
本题考查了整式的化简求值，能熟记乘法公式是解此题的关键．
17.【答案】证明：∵点B为线段AC的中点，
∴AB=BC，
∵AD/​/BE，
∴∠A=∠EBC，
∵BD/​/CE，
∴∠C=∠DBA，
在△ABD与△BCE中，
∠A=∠EBCAB=BC∠DBA=∠C，
∴△ABD≌△BCE(ASA)．
【解析】根据ASA判定定理直接判定两个三角形全等．
本题主要考查了全等三角形的判定，熟练掌握全等三角形的判定定理是解题的关键．
18.【答案】解：2(x−2y)2−(2y+x)(−2y+x)
=2(x2−4xy+4y2)−(x2−4y2)
=2x2−8xy+8y2−x2+4y2
=x2−8xy+12y2，
当x=−1，y=−2时，原式=(−1)2−8×(−1)×(−2)+12×(−2)2
=1−16+48
=33．
【解析】先去括号，再合并同类项，然后把x，y的值代入化简后的式子进行计算即可解答．
本题考查了整式的混合运算−化简求值，准确熟练地进行计算是解题的关键．
19.【答案】证明：∵将线段BE绕点B按逆时针方向旋转70°得到线段BF，
∴BE=BF，∠EBF=70°，
∵∠ABC=70°，
∴∠EBF=∠ABC，
∴∠DBF=70°−∠ABE=∠CBE，
在△BCE与△BDF中，
BE=BF∠CBE=∠DBFBC=BD，
∴△BCE≌△BDF(SAS)．
【解析】由旋转的性质知BE=BF，∠EBF=70°，再利用SAS即可证明结论．
本题主要考查了旋转的性质，全等三角形的判定与性质，熟练掌握旋转前面对应边相等是解题的关键．
20.【答案】证明：∵∠DAB=∠EAC，
∴∠DAB+∠BAC=∠EAC+∠BAC，
即∠DAC=∠BAE，
在△ACD和△AEB中，
AD=AB∠DAC=∠BAEAC=AE，
∴△ACD≌△AEB(SAS)．
【解析】先证明∠DAC=∠BAE，然后根据“SAS”可判断△ACD≌△AEB．
本题考查了全等三角形的判定：熟练掌握全等三角形的5种判定方法是解决问题的关键，选用哪一种方法，取决于题目中的已知条件．
21.【答案】解：(1)在Rt△CDB中，
由勾股定理得，CD2=BC2−BD2=252−152=400，
所以，CD=20(负值舍去)，
所以，CE=CD+DE=20+1.6=21.6(米)，
答：风筝的高度CE为21.6米；
(2)由题意得，CM=12米，
所以DM=8米，
所以BM= DM2+BD2= 82+152=17(米)，
所以BC−BM=25−17=8(米)，
所以他应该往回收线8米．
【解析】(1)利用勾股定理求出CD的长，再加上DE的长度，即可求出CE的高度；
(2)根据勾股定理即可得到结论．
本题考查了勾股定理的应用，熟悉勾股定理，能从实际问题中抽象出勾股定理是解题的关键．
22.【答案】解：(1)如：38+3−8=2+(−2)=0，则(38)3+(3−8)3=8+(−8)=0，即8和−8互为相反数，
∴”如果两数的立方根互为相反数，那么这两个数也互为相反数“的结论成立；
(2)∵37−y和32y−5互为相反数，
∴37−y+32y−5=0，
∴(37−y)3+(32y−5)3=0，
7−y+2y−5=0，
y=−2，
∵0的平方根是它本身，x−3的平方根是它本身，
∴x−3=0，x=3，
∴x+y=−2+3=1，
∴x+y的立方根是1．
【解析】(1)根据已知条件，举出一个例子，通过计算进行验证即可；
(2)根据已知条件的结论，列出关于y的方程，求出y，再根据平方根是它本身的数是0，列出关于x的方程，求出x，从而求出x+y，最后求出答案即可．
本题主要考查了平方根和立方根，解题关键是理解已知条件中的结论，并能够进行验证．
23.【答案】证明：在Rt△ABD与Rt△AED中，
AD=ADBD=ED,
∴Rt△ABD≌Rt△AED(HL)，
∴∠BAD=∠EAD，
∵AB/​/CD，
∴∠BAD=∠ADC，
∴∠EAD=∠ADC，
∵∠AFC=∠EAD+∠ADC，
∴∠AFC=2∠ADC．
【解析】本题考查了全等三角形的判定与性质，平行线的性质，三角形外角的性质，熟练掌握全等三角形的判定与性质是解题的关键．
根据HL证明Rt△ABD≌Rt△AED，得出∠BAD=∠EAD，再由AB/​/CD可推出∠EAD=∠ADC，最后根据三角形的外角的性质即可得出结论．