

专题7可能性(统计与概率)-2023-2024学年五年级上册数学寒假专项提升(北师大版)
展开一、选择题
1.(2022上·陕西西安·五年级统考期末)花生猴从一个装有红、黄两种颜色球的盒子里任意摸一个球,摸了100次,摸到红球63次,黄球37次,下列说法正确的是( )。
A.盒子里装了100个球B.盒子里的红球多的可能性大
C.盒子里的红球一定多D.盒子里的红球和黄球一样多
2.(2022上·四川成都·五年级统考期末)奇思和妙想做摸球游戏,每次任意摸一个球,然后放回再摇匀,每人摸10次。摸到白球妙想得1分,摸到黄球奇思得1分,摸到其他颜色的球二人都不得分。你认为从( )个口袋里摸球是公平的。
A.B.
C.D.
3.(2021上·广东揭阳·五年级统考期末)一个正方体的六个面上标有1,2,3,4,5,6。甲、乙两人任意掷出正方体后,若朝上的数字大于3,则甲获胜;若朝上的数字小于3,则乙获胜。这个游戏( )。
A.公平B.不公平C.可能性一样D.无法确定
4.五年级45名同学玩摸球游戏(每人摸一次,然后放回摇匀),摸球结果如下表。箱子里最有可能装有( )。
A.8个白球和2个黄球B.5个白球和5个黄球
C.2个白球和8个黄球D.21个白球和19个黄球
5.(2022上·陕西延安·五年级校考期中)纸袋中有黑白两种颜色的棋子,从中摸40次(摸出一个棋子后再放回去摇匀),有35次摸到白棋子,5次摸到黑棋子,纸袋中( )。
A.黑棋子一定少B.白棋子一定多
C.白棋子可能多D.以上都不对
6.(2022上·山西运城·五年级统考期末)盒中装有黑、白两种颜色的球(除了颜色不同,其他都相同),笑笑每次从中摸出一个球,记录下它的颜色,再放回去摇匀,重复40次,试验结果如图。笑笑最有可能是用下面( )盒做的试验。
A. B. C. D.
二、填空题
7.(2022上·河南鹤壁·五年级统考期末)清幽别苑在开盘当天,举行了摸球赢大奖活动。购房者凭购房发票可摸四次,每次摸一个球,只要摸到写有“清幽别苑”4个字的球,便可赢得一辆小轿车。乐乐在摸奖箱旁随机调查了50人,这50人共摸了200次,情况如下:
根据调查数据推测,奖箱中写有“( )”字的球可能最多,写有“( )”字的球可能最少,( )赢得一辆小轿车(填“容易”或“不容易”)。
8.(2023上·陕西宝鸡·五年级统考期中)在一个袋子中装有同样大小的棋子,其中红色的有5枚,白色的有3枚,黑色的有2枚。
(1)任意摸出一枚,( )棋子的可能性最大,( )棋子的可能性最小。
(2)一次性摸出6枚,其中一定有( )棋子。
9.(2023上·山西吕梁·五年级统考期中)某奶茶店准备设计100张抽奖券进行促销。老板想让抽到“免费品尝”的可能性最小,抽到“立减1元”的可能性最大,抽到“第二杯半价”和“立减5元”的可能性相同。如果请你设计这100张奖券,你会怎样分配?把你的想法填在如表中。
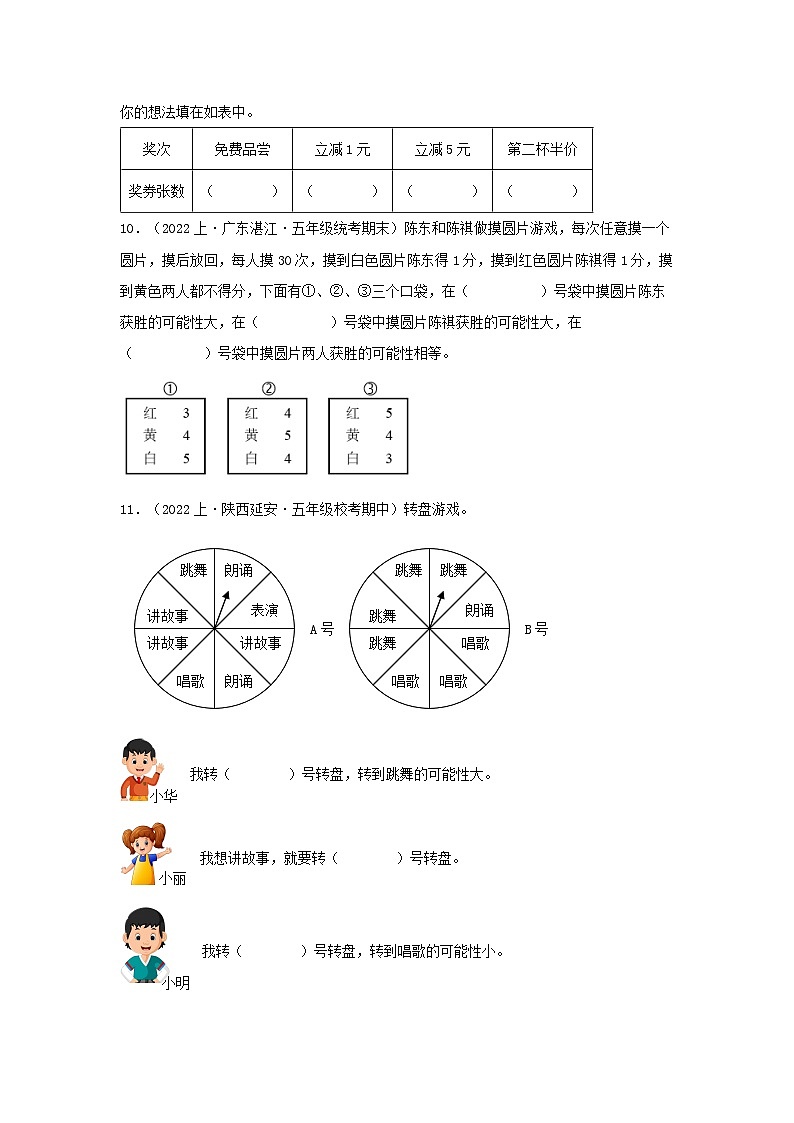
10.(2022上·广东湛江·五年级统考期末)陈东和陈祺做摸圆片游戏,每次任意摸一个圆片,摸后放回,每人摸30次,摸到白色圆片陈东得1分,摸到红色圆片陈祺得1分,摸到黄色两人都不得分,下面有①、②、③三个口袋,在( )号袋中摸圆片陈东获胜的可能性大,在( )号袋中摸圆片陈祺获胜的可能性大,在( )号袋中摸圆片两人获胜的可能性相等。
11.(2022上·陕西延安·五年级校考期中)转盘游戏。
A号B号
我转( )号转盘,转到跳舞的可能性大。
我想讲故事,就要转( )号转盘。
我转( )号转盘,转到唱歌的可能性小。
12.下面的游戏规则公平吗?在括号里填上“公平”或“不公平”。
(1)投骰子,点数为奇数,小红赢;点数为偶数,小枫赢。( )
(2)投骰子,每人投一次,谁投的点数大谁赢,如果点数相同则重新投。( )
(3)选出扑克牌中同一花色的13张牌,反扣在桌面上,任意摸一张,点数大于10,小红赢;点数小于10,小刚赢。( )
三、连线题
13.从每个纸箱里任意摸出一个球,结果可能是什么?连一连。
四、作图题
14.(2023上·山西吕梁·五年级统考期中)按要求涂色或标字。
(1)涂色:使图①摸出的一定是黑色小球。
(2)标字:使图②摸出红色小圆柱的可能性最大,摸出蓝色小圆柱与黄色小圆柱的可能性相等且不为0。
(3)标字:使图③指针只可能停在红色、蓝色或绿色区域,并且停在红色区域的可能性最大,停在蓝色区域的可能性最小。
五、解答题
15.(2022上·陕西咸阳·五年级统考期末)某小学举办了主题为“小学生要不要参加课外实践活动”的辩论比赛,张老师通过抽下面的数字卡片来决定三(1)班和三(2)班谁是正方。张老师抽到卡片上的数是奇数,三(1)班是正方;抽到卡片上的数是偶数,三(2)班是正方,这个游戏公平吗?为什么?如果不公平,请你设计一个对双方都公平的游戏规则。
16.与同桌玩“石头、剪子、布”游戏,总共玩40次。
(1)记录并统计游戏结果。
(2)这个游戏究竟公平不公平呢?我们可以这样想。
我如果出“石头”,结果会有( )种可能。因为:
如果同桌出“石头”,平;
如果同桌出“布”,输;
如果同桌出“剪子”,赢。
同样,我如果出“布”,结果有( )种可能;如果出“剪子”,结果有( )种可能。
因此,结果一共有( )种可能,每一种结果出现的可能性相等,因此,游戏是公平的。
17.明明和乐乐一起玩跳棋,由莹莹设计规则决定他们谁先走。这个规则公平吗?为什么?
18.(2022上·山西运城·五年级统考期末)奇思和妙想玩转盘游戏,他们约定:指针停在白色区域,奇思赢;指针停在阴影区域,妙想赢。
(1)如果玩一次转盘游戏,妙想一定会赢吗?为什么?
(2)请你用下面的转盘,重新设计一个对双方都公平的游戏规则。
19.(2022上·陕西渭南·五年级统考期中)挪硬币。
掷一枚硬币,既可能出现正面朝上,也可能出现反面朝上。出现正面朝上和反面朝上的可能性一样大吗?下表是一些著名的数学家做试验记录的结果。
(1)圈出括号里正确的选项。
通过试验发现:当人们大量重复掷一枚硬币时,正面朝上和反面朝上的次数(很接近、相差很远),所以在足球比赛前采用掷硬币来决定谁开球的规则是(不公平、公平)。
(2)掷一枚硬币,正面朝上的可能性和反面朝上的可能性( )。
20.(2021上·辽宁大连·五年级统考期末)奇思和妙想做摸牌游戏,他们选出点数分别为1,2,3,4的扑克牌各一张,反扣在桌面上。每次摸两张,然后放回去,另一个人再摸。两张牌点数之和大于5,奇思赢;小于5,妙想赢,这个游戏规则公平吗?为什么?(写一写)
参考答案
1.B
【分析】从球的数量上分析,数量最多的,摸到的可能性最大,数量最少的,摸到的可能性最小,数量相等的,摸到的可能性一样。
【详解】A.盒子里球的个数不确定是100个,所以说法错误,故不符合题意;
B.摸到红球次数大于黄球次数,那么盒子里红球多的可能性大,所以说法正确,故符合题意;
C.盒子里红球不一定多,所以说法错误,故不符合题意;
D.盒子里的红球和黄球不一定一样多,所以说法错误,故不符合题意。
故答案为:B。
【分析】本题考查了可能性的大小,摸到哪种颜色球的次数多,则盒子里的哪种颜色球多的可能性大。
2.A
【分析】不论盒子里有几种颜色的球,必须有白球、黄球。要想游戏规则公平,白球、黄球的个数必须相同。
【详解】奇思和妙想做摸球游戏,每次任意摸一个球,然后放回再摇匀,每人摸10次。摸到白球妙想得1分,摸到黄球奇思得1分,摸到其他颜色的球二人都不得分。“我”认为从口袋里摸球是公平的。
故答案为:A
【分析】判断游戏规则是否公平的关键是看参与游戏的各方出现的可能性是否相同,相同规则公平,否则规则不公平。
3.B
【分析】由题意可知,一个正方体掷出的数字一共有6种情况,朝上的数字大于3,则甲获胜,那么甲获胜有3种可能;若朝上的数字小于3,则乙获胜,那么乙获胜有2种可能,由此即可判断。
【详解】朝上的数字大于3的有4、5、6三种可能,朝上的数字小于3的有1、2两种可能,3>2,所以甲获胜的可能性大,游戏不公平。
故答案为:B
【分析】本题主要考查可能性的大小判断,总情况相同的时候,那么谁占的情况种类越多,获胜的可能性越大。
4.C
【分析】不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。所以摸到白球的次数小于黄球的次数,摸到白球的可能性小于摸到黄球的可能性,则白球的个数小于黄球的个数。据此解答。
【详解】10<35
摸到白球的次数小于黄球的次数,则白球的个数小于黄球的个数;
A.8>2
8个白球和2个黄球不符合题意;
B.5=5
5个白球和5个黄球不符合题意;
C.2<8
2个白球和8个黄球符合题意;
D.21>19
21个白球和19个黄球不符合题意。
故答案为:C
【分析】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关。
5.C
【分析】根据数量的多少可以判断可能性,数量越多,摸到的可能性越大,数量越少,摸到的可能性就越小,据此分析做出判断即可。
【详解】纸袋中有黑白两种颜色的棋子,从中摸40次(摸出一个棋子后再放回去摇匀),有35次摸到白棋子,5次摸到黑棋子,35>5,说明白色棋子可能多,因为事件不确定的,所以不能说明黑色棋子一定少,白色棋子一定多,
故答案为:C
【分析】解答本题的关键是要学生理解是的可能性,而不是一定性。
6.C
【分析】从球的数量上分析:数量多的,摸到的可能性大;数量少的,摸到的可能性小;数量相等的,摸到的可能性一样。本题中摸到黑球的次数多,摸到黑球的可能性大,说明盒中黑球的个数多,白球的个数少,据此判断。
【详解】A.盒子中只有白球,没有黑球,不符合题意;
B.盒子中有黑色球有3个,白球有7个,7>3,白球比较多,不符合题意;
C.盒子中有黑色球有8个,白球有2个,8>2,黑球比较多,符合题意;
D.盒子中只有黑球,没有白球,不符合题意。
故答案为:C
【分析】解答本题的关键是掌握可能性大小的判断方法。
7.别 清 不容易
【分析】比较四个字球摸到的数量,哪个字球的数量多,摸到哪个字球的可能性就大,哪个字球数量少,摸到哪个字球的可能性就小,据此解答。
【详解】2<13<35<150,即清<苑<幽<别;“别”字球可能最多,“清”球可能最少。
清幽别苑在开盘当天,举行了摸球赢大奖活动。购房者凭购房发票可摸四次,每次摸一个球,只要摸到写有“清幽别苑”4个字的球,便可赢得一辆小轿车。乐乐在摸奖箱旁随机调查了50人,这50人共摸了200次,情况如下:
根据调查数据推测,奖箱中写有“别”字的球可能最多,写有“清”字的球可能最少,不容易赢得一辆小轿车。
【分析】本题考查可能性大小,在大小形状相同的情况下,哪种求的数量最多,摸到的可能性就越大。
8.(1)红色 黑色
(2)红色
【分析】(1)根据题意,盒子里有三种颜色的棋子,那么任意摸出1个棋子,就有可能摸到这三种颜色中的任何一个,所以三种颜色的棋子都有可能摸到。根据可能性大小的判断方法,比较盒子里三种颜色棋子的数量多少,数量最多的,摸到的可能性最大;数量最小的,摸到的可能性最小。
(2)红色的有5枚,白色的有3枚,黑色的有2枚,摸出6枚时超出黑色和白色的数量之和,要摸6枚,则肯定要有红色的棋子,所以其中一定有红色的棋子,据此解答即可。
【详解】(1)5>3>2
任意摸出一枚,红色棋子的可能性最大,黑色棋子的可能性最小。
(2)3+2=5(枚)
6>5
所以一次性摸出6枚,其中一定有红色棋子。
9.10;50;20;20
【分析】哪种奖券的数量最少,抽到哪种奖券的可能性就最小;哪种奖券的数量最多,抽到哪种奖券的可能性就最大;数量相同的奖券,抽到的可能性相同,据此分析。
【详解】
(答案不唯一)
10.① ③ ②
【分析】①袋子中红色圆片3个,黄色圆片4个,白色圆片5个,摸到白色圆片的可能性大,就是陈东获胜可能性大,②袋子中红色圆片4个,黄色圆片5个,白色圆片4个,摸到红色圆片和白色圆片的可能性一样大,就是两人获胜机会相等;③袋子中红色圆片5个,黄色圆片4个,白色圆片3个,摸到红色圆片的可能性大,就是陈祺获胜可能性大。
【详解】陈东和陈祺做摸圆片游戏,每次任意摸一个圆片,摸后放回,每人摸30次,摸到白色圆片陈东得1分,摸到红色圆片陈祺得1分,摸到黄色两人都不得分,下面有①、②、③三个口袋,在①号袋中摸圆片陈东获胜的可能性大,在③号袋中摸圆片陈祺获胜的可能性大,在②号袋中摸圆片两人获胜的可能性相等。
【分析】此题主要考查对事件可能性大小的理解和运用。
11.B A A
【分析】A号转盘有多种结果,讲故事占其中的,朗诵占,跳舞、唱歌、表演各占,>>,转到讲故事的可能性比较大,转动跳舞、歌唱、表演的可能性较小;
B号转盘有三种结果,跳舞占其中的,唱歌占,朗诵占,>>,转到跳舞的可能性大,转到朗诵的可能性小,据此解答。
【详解】根据分析可知,,我转B号盘,转到跳舞的可能性大。
,我想讲故事,就要转A号盘。
,我转A号转盘,转到唱歌的可能性小。
【分析】本题考查可能性的大小,根据各自占的分率,进行比较解答。
12.(1)公平
(2)公平
(3)不公平
【分析】确定一个游戏是否公平,要先找出事件发生的所有可能,然后看对于游戏双方,获胜的可能性是否相同。若相同,则游戏规则公平;若不相同,则游戏规则不公平。据此解答。
【详解】(1)骰子上有6种点数,其中1、3、5点为奇数,2、4、6点为偶数,奇数和偶数的数量相等,则投出奇数和偶数的可能性相等,即小红和小枫赢的可能性相等,所以这个游戏规则公平。
(2)骰子上有6种点数,每人投一次,投出的点数都有6种可能,这时谁投的点数大谁赢,如果点数相同则重新投,游戏规则公平。
(3)同一花色的13张牌中,大于10的点数有11、12、13,共3张;小于10的点数有1~9,共9张。则摸到大于10和小于10的牌可能性不同,即小红和小刚赢的可能性不相同,这个游戏规则不公平。
【分析】本题考查游戏规则的公平性。找出游戏发生的所有可能结果是解题的关键。
13.见详解
【分析】不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小,数量相同,可能性也相同。
【详解】10个白球不可能摸到红球;
8白2红中,摸到白球的可能性比红球大;
3白7红中,摸到红球的可能性比白球大;
10个红球中,一定能摸到红球。
连线如下:
【分析】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小,数量相同,可能性也相同。
14.见详解
【分析】(1)盒子里全都是黑色小球,摸出的一定是黑色小球,全部涂成黑色即可;
(2)盒子里有红色也有蓝色和黄色小圆柱,红色小圆柱最多,摸出红色小圆柱的可能性就最大,蓝色和黄色小圆柱的数量相等,则摸出蓝色小圆柱与黄色小圆柱的可能性相等,据此涂色;
(3)哪种颜色的区域最多,指针停在哪种颜色区域的可能性最大,哪种颜色的区域最少,指针停在哪种颜色区域的可能性最小,据此涂红色、蓝色和绿色,且涂的红色区域最多,蓝色区域最少即可。
【详解】
(图③涂法不唯一)
15.见详解
【分析】游戏规则的公平性就是指对游戏的双方来说,机会是均等的,也就是双方获胜的可能性的大小相等。确定一个游戏是否公平,要先找出事件发生的所有可能,然后看对于游戏双方,获胜的可能性是否相同。若相同,则游戏规则公平;若不相同,则游戏规则不公平。
观察这组数字可知,共有7个数字,比4的的数有3个,比4小的数有3;所以我设计的游戏规则是:任抽一张,抽出的数小于4,则三(1)班是正方;抽出的数大于4,则三(2)班是正方;抽出的数等于4,则放回重新抽。
【详解】,观察这组数字可知,奇数有4个、偶数有3个,因为:4>3,所以,这个游戏是不公平的。
答:这个游戏是不公平的,因为抽到奇数的机会比抽到偶数的机会大。我设计的游戏规则是:任抽一张,抽出的数小于4,则三(1)班是正方;抽出的数大于4,则三(2)班是正方;抽出的数等于4,则放回重新抽。
【分析】判断游戏规则是否公平的关键是看参与游戏的各方获胜的可能性是否相同。
16.(1)见详解;(2)3;3;3;3
【分析】(1)和同桌玩40次“石头、剪子、布”游戏,如实记录并填表即可。
(2)不论我出什么,同桌只有3种出法,对应3种输赢结果,那么每种结果的可能性是一样的,那么游戏是公平的。
【详解】(1)如表:
记录并统计游戏结果。
(答案不唯一)
(2)我如果出“石头”,结果会有3种可能。因为:
如果同桌出“石头”,平;
如果同桌出“布”,输;
如果同桌出“剪子”,赢。
同样,我如果出“布”,结果有3种可能;如果出“剪子”,结果有3种可能。
因此,结果一共有3种可能,每一种结果出现的可能性相等,因此,游戏是公平的。
【分析】本题考查了可能性,掌握可能性大小的判断方法是解题的关键。
17.不公平;理由见详解
【分析】骰子有1,2,3,4,5,6一共有6个数字,判断游戏是否公平,就看明明和乐乐获胜的机会是否相同,如果获胜的机会相同,游戏公平,否则,就不公平,据此解答。
【详解】骰子有1,2,3,4,5,6一共有6个数字,点数大于4的有5,6一共2个;
点数小于4的1,2,3,一共有3个;
3>2,乐乐获胜的机会大,明明获胜的机会小,游戏不公平。
答:不公平;因为点数大于4的只有2个,点数小于4的有3个,所以不公平。
【分析】本题考查游戏的公平性,只要获胜的机会相同,游戏才公平。
18.(1)见详解
(2)见详解
【分析】(1)根据可能性可知,圆盘有2种颜色,有白色区域和阴影区域,转盘转动,指针停在区域有两种情况,可能停在白色区域,也可能性停在阴影区域,白色区域小于阴影区域,阴影区域赢的可能性大,但不一定会赢,据此解答;
(2)要使游戏公平,则两个人的赢的区域面积应该一样大,据此解答。
【详解】(1)根据分析可知,转盘有两种颜色,指针可能停在白色区域,也可能停在阴影区域,所以如果玩一次转盘游戏,妙想不一定会赢。
(2)转盘一共分成9等份,如果指针转到1,两人谁也不赢,其余剩下的8份其中的4份涂色,4份空白,即游戏公平(答案不唯一)。
【分析】本题主要考查可能性的大小,熟练掌握可能性大小的判断方法并灵活运用。
19.(1)见详解
(2)相等
【分析】抛掷一枚硬币,可能面朝上,也可能面朝下,两种可能性的大小相等;据此解答。
【详解】(1)通过试验发现:当人们大量重复掷一枚硬币时,正面朝上和反面朝上的次数,所以在足球比赛前采用掷硬币来决定谁开球的规则是。
(2)掷一枚硬币,正面朝上的可能性和反面朝上的可能性相等。
【分析】本题考查了可能性,掌握可能性大小的判断方法是解题的关键。
20.公平;理由见详解
【分析】游戏规则的公平性就是指对游戏的双方来说,机会是均等的,也就是双方获胜的可能性的大小相等。确定一个游戏是否公平,要先找出事件发生的所有可能,然后看对于游戏双方,获胜的可能性是否相同。若相同,则游戏规则公平;若不相同,则游戏规则不公平。
【详解】点数为1,2,3,4的扑克牌各1张。两张牌上的点数的和有:1+2=3,1+3=4,1+4=5,2+3=5,2+4=6,3+4=7,1+1=2,2+2=4,3+3=6,4+4=8。这个游戏规则公平理由:其中大于5的有6、6、7、8共四种可能,小于5的有2、3、4、4四种可能,因此,游戏规则是公平的。
【分析】此题主要考查游戏规则的公平性,判断游戏规则是否公平,就要计算每个参与者取胜的可能性,可能性相等就公平,否则就不公平。颜色
白球
黄球
次数
10
35
颜色
记录
黑
正正正正正正
白
正正
摸到的字
清
幽
别
苑
次数
2
35
150
13
奖次
免费品尝
立减1元
立减5元
第二杯半价
奖券张数
( )
( )
( )
( )
结果
输
赢
平
次数/次
试验者
掷硬币次数
正面朝上次数
反面朝上次数
德•摩根
4092
2048
2044
蒲丰
4040
2048
1992
费勒
10000
4979
5021
皮尔逊
24000
12012
11988
罗曼诺夫斯基
80640
39699
40941
摸到的字
清
幽
别
苑
次数
2
35
150
13
奖次
免费品尝
立减1元
立减5元
第二杯半价
奖券张数
10
50
20
20
结果
输
赢
平
次数/次
13
14
13
专题7可能性(统计与概率)-2023-2024学年四年级上册数学寒假专项提升(苏教版): 这是一份专题7可能性(统计与概率)-2023-2024学年四年级上册数学寒假专项提升(苏教版),共13页。试卷主要包含了选择题,填空题,连线题,作图题,解答题等内容,欢迎下载使用。
专题8统计表和条形统计图(二)(统计与概率)-2023-2024学年五年级上册数学寒假专项提升(苏教版): 这是一份专题8统计表和条形统计图(二)(统计与概率)-2023-2024学年五年级上册数学寒假专项提升(苏教版),共25页。试卷主要包含了选择题,填空题,四年级参加兴趣小组人数统计表,解答题等内容,欢迎下载使用。
专题7多边形的面积(图形与几何)-2023-2024学年五年级上册数学寒假专项提升(苏教版): 这是一份专题7多边形的面积(图形与几何)-2023-2024学年五年级上册数学寒假专项提升(苏教版),共12页。试卷主要包含了选择题,填空题,计算题,作图题,解答题等内容,欢迎下载使用。













