

2022-2023学年河南省驻马店市泌阳县九年级(上)期末数学试卷(含解析)
展开1.下面是最简二次根式的是( )
A. a2+1B. 12C. 8D. 27
2.若关于x的一元二次方程ax2+bx+5=0(a≠0)的一个解是x=−1,则2017−a+b的值是( )
A. 2016B. 2018C. 2020D. 2022
3.如图,在△ABC中,DE//BC,若ADAB=35,则AECE的值为( )
A. 3
B. 23
C. 32
D. 53
4.如图所示的是一段索道的示意图.已知A、B两点间的距离为50米,∠BAC=α,则缆车从A点到B点上升的高度(即BC的长)为( )
A. 50sinα米B. 50sinα米C. 50csα米D. 50csα米
5.下列判断正确的是( )
A. 任意掷一枚质地均匀的硬币10次,一定有5次正面向上
B. 天气预报说“明天的降水概率为40%”,表示明天有40%的时间都在降雨
C. “任意购买一张电影票,座位号是3的倍数”为随机事件
D. “概率为0.0001的事件”是不可能事件
6.已知(−2,y1)、(12,y2),(1,y3)是二次函数y=12x2+x+c图象上的三点,则y1、y2、y3的大小关系为( )
A. y3>y2>y1B. y3
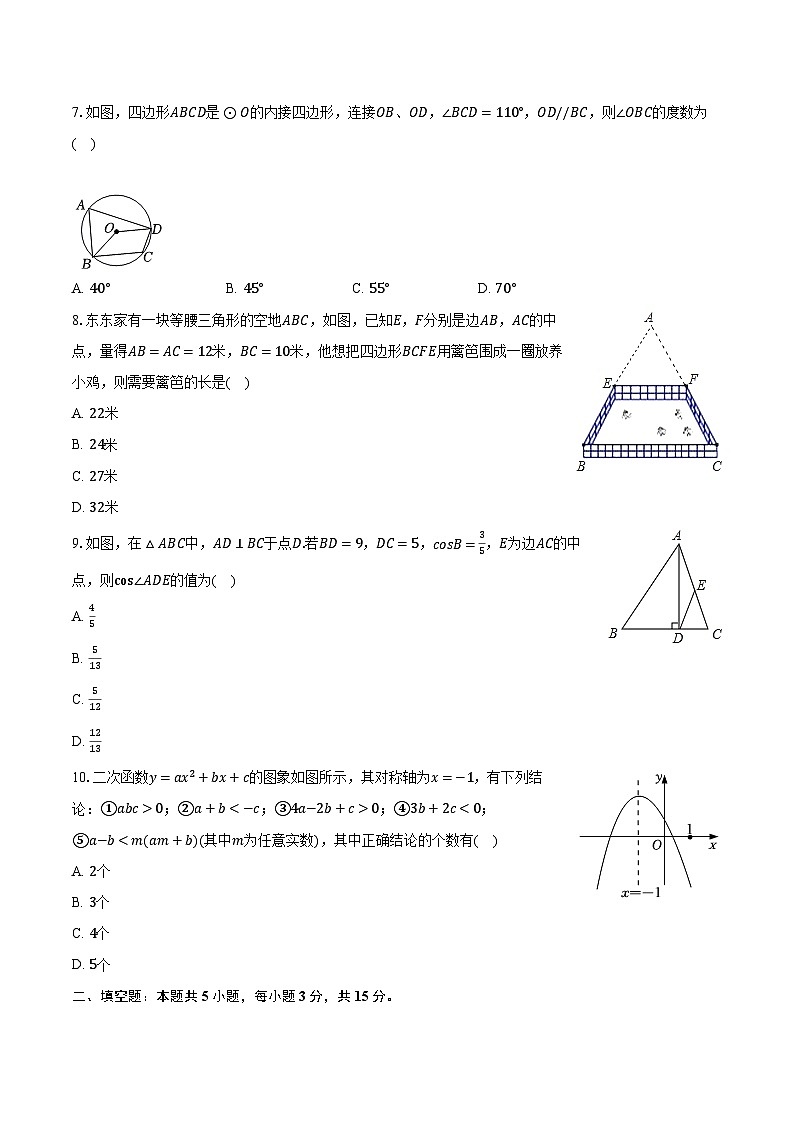
A. 40°B. 45°C. 55°D. 70°
8.东东家有一块等腰三角形的空地ABC,如图,已知E,F分别是边AB,AC的中点,量得AB=AC=12米,BC=10米,他想把四边形BCFE用篱笆围成一圈放养小鸡,则需要篱笆的长是( )
A. 22米
B. 24米
C. 27米
D. 32米
9.如图,在△ABC中,AD⊥BC于点D.若BD=9,DC=5,csB=35,E为边AC的中点,则cs∠ADE的值为( )
A. 45
B. 513
C. 512
D. 1213
10.二次函数y=ax2+bx+c的图象如图所示,其对称轴为x=−1,有下列结论:①abc>0;②a+b<−c;③4a−2b+c>0;④3b+2c<0;⑤a−b
B. 3个
C. 4个
D. 5个
二、填空题:本题共5小题,每小题3分,共15分。
11.已知xy=45,则x+yy=______.
12.如图,在8×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为______.
13.泌阳县因位于泌水之阳(山南水北为阳)而得名,境内自然景观众多,不仅有雄奇险秀的铜山、驻马店市山峰之最的白云山、中原盘古圣地盘古山,还有默默无闻的弥勒佛祖道场罗汉山.某中学九年级学生小明和小华两人计划在寒假期间随机从这四个景点中随机选择一个去爬山游玩,两人恰好选择同一景点的概率是______ .
14.如图所示,抛物线y=ax2+bx+c的顶点为点P(−2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P由(−2,2)移动到P(1,−1),此时抛物线与y轴交于点A′,则AA′的长度为______.
15.如图,在矩形ABCD中,AD=4,AB=6,若E,F分别是AD,DC边上的动点,且AE:DF=3:2,AF与BE交于点P,连接DP.则DP的最小值为______ .
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.(本小题10分)
(1)计算:( 3−1)⋅( 3+1)− 27+6 13;
(2)计算:sin30°⋅tan45°+sin260°−2cs60°.
17.(本小题9分)
某校英语社团举行了“单词听写大赛”,每位参赛选手共听写单词100个.现从参加比赛的男女选手中分别随机抽取部分学生进行调查,对答对的情况进行分组如下:A组:x<60,B组:60≤x<70,C组:70≤x<80,D组:80≤x<90,E组:90≤x≤100.并绘制了如下不完整的统计图:
请根据以上信息解答下列问题:
(1)本次调查共抽取了多少名学生,并将条形统计图补充完整;
(2)求出A组所对的扇形圆心角的度数;
(3)若从D、E两组中分别抽取一位学生进行采访,请用画树状图或列表法求出恰好抽到两位女学生的概率.
18.(本小题9分)
已知关于x的一元二次方程x2+(m+3)x+m+2=0.
(1)求证:无论m取何值,原方程总有两个实数根;
(2)若x1,x2是原方程的两根,且x12+x22=2,求m的值.
19.(本小题9分)
如图,某数学课外活动小组利用课余时间,测量了安装在一幢楼房顶部的公益广告牌的高,如图,DM为楼房的高,且C,D,M三点共线,在楼房的侧面A处,测得点C与点D的仰角分别为45°和37.3°,BM=15米,根据以上测得的相关数据,求这个广告牌的高(CD的长)(结果精确到0.1米,参考数据:sin37.3°≈≈0.7955,tan37.3°≈0.7618)
20.(本小题9分)
为了落实劳动教育,某学校邀请农科院专家指导学生进行小番茄的种植,经过试验,其平均单株产量y千克与每平方米种植的株数x(2≤x≤8,且x为整数)构成一种函数关系.每平方米种植2株时,平均单株产量为4千克;以同样的栽培条件,每平方米种植的株数每增加1株,单株产量减少0.5千克.
(1)求y关于x的函数表达式.
(2)每平方米种植多少株时,能获得最大的产量?最大产量为多少千克?
21.(本小题9分)
如图①,一个可调节高度的喷灌架喷射出的水流可以近似地看成抛物线.图②是喷射出的水流在平面直角坐标系中的示意图,其中喷灌架置于点O处,喷水头的高度(喷水头距喷灌架底部的距离)设置的是1米,当喷射出的水流距离喷水头水平距离为8米时,达到最大高度5米.
(1)求水流运行轨迹的函数解析式;
(2)若在距喷灌架12米处有一棵3.5米高的果树,问:水流是否会碰到这棵果树?请通过计算说明.
22.(本小题10分)
如图,AB是⊙O的直径,C、D为⊙O上的点,且BC//OD,过点D作DE⊥AB于点E.
(1)求证:BD平分∠ABC;
(2)若BC=4,DE=3,求⊙O的半径长.
23.(本小题10分)
感知:
(1)数学课上,老师给出了一个模型:如图1,∠BAD=∠ACB=∠AED=90°,由∠1+∠2+∠BAD=180°,∠2+∠D+∠AED=180°,可得∠1=∠D;又因为∠ACB=∠AED=90°,可得△ABC∽△DAE,进而得到BCAC=______.我们把这个数学模型称为“一线三等角”模型.
应用:
(2)实战组受此模型的启发,将三等角变为非直角,如图2,在△ABC中,点D在边BC上,并且DA=DE,∠B=∠ADE=∠C.若BC=a,AB=b,求CE的长度(用含a,b的代数式表示).
拓展:
(3)创新组突发奇想,将此模型迁移到平行四边形中,如图3,在▱ABCD中,E为边BC上的一点,F为边AB上的一点.若∠DEF=∠B.求证:AB⋅FE=BE⋅DE.
答案和解析
1.【答案】A
【解析】解:A、 a2+1是最简二次根式,故A符合题意.
B、原式= 22,故B不符合题意.
C、原式=2 2,故C不符合题意.
D、原式=3 3,故D不符合题意.
故选:A.
最简二次根式的概念:(1)被开方数不含分母;(2)被开方数中不含能开得尽方的因数或因式.
本题考查最简二次根式,解题的关键是正确理解最简二次根式的概念,本题属于基础题型.
2.【答案】D
【解析】解:把x=−1代入ax2+bx+5=0(a≠0),得
∴a−b+5=0,
∴a−b=−5,
∴原式=2017−(a−b)
=2017−(−5)
=2022.
故选:D.
把x=−1代入原方程可得a−b=−5,然后代入2017−a+b即可求出原式的值.
本题考查一元二次方程的解,解题关键是熟练运用一元二次方程的解的概念,本题属于基础题型.
3.【答案】C
【解析】解:∵DE//BC,
∴AEAC=ADAB=35,
∴AECE=32,
故选:C.
直接利用平分线分线段成比例定理求解.
本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.
4.【答案】A
【解析】解:如图,在Rt△ABC中,∠ACB=90°,∠BAC=α,
∴sinα=BCAB,
∴BC=AB⋅sinα,
∵AB=50米,
∴BC=50sinα米,
故选:A.
在Rt△ABC中,∠ACB=90°,斜边AB是已知边,∠BAC是已知角,而要求的是∠BAC的对边BC的长,所以选择∠BAC的正弦,即可求出结果.
此题考查锐角三角函数、解直角三角形等知识与方法,解题的关键是正确掌握锐角三角函数的定义,选择适当的锐角三角函数模型.
5.【答案】C
【解析】解:A.投掷硬币是随机事件,每次正面的概率是12,但任意掷一枚质地均匀的硬币10次,不一定有5次正面向上,说法错误,故本选项不符合题意;
B.明天的降水概率为40%,只能说明明天有40%的机会降雨,说法错误,故本选项不符合题意;
C.“任意购买一张电影票,座位号是3的倍数”为随机事件,说法正确,故本选项符合题意;
D.“概率为0.0001的事件”是事件事件,说法错误,故本选项不符合题意.
故选:C.
根据概率的意义、随机事件的概念解答即可.
本题考查了概率的意义以及随机事件,概率是频率(多个)的波动稳定值,是对事件发生可能性大小的量的表现.概率取值范围:0≤p≤1.
6.【答案】A
【解析】解:∵y=12x2+x+c,
∴二次函数y=12x2+x+c图象的对称轴为直线x=−12×12=−1,开口向上,
∵点(−2,y1)到直线x=−1的距离最近,点(1,y3)到直线x=−1的距离最远,
∴y3>y2>y1.
故选:A.
先根据二次函数的性质得到抛物线的对称轴为直线x=−1,然后通过比较三个点到对称轴的远近确定函数值的大小.
本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了二次函数的性质.
7.【答案】A
【解析】解:∵四边形ABCD是⊙O的内接四边形,
∴∠A=180°−∠BCD=70°,
∴∠BOD=2∠A=140°,
∵OD//BC,
∴∠BOD+∠OBC=180°,
∴∠OBC=180−∠BOD=180°−140°=40°,
故选:A.
根据圆内接四边形的性质和圆心角与圆周角的关系求出∠BOD,根据平行线的性质即可求出∠OBC的度数.
本题考查的是圆内接四边形的性质,掌握圆内接四边形的对角互补是解题的关键.
8.【答案】C
【解析】解:∵E,F分别是边AB,AC的中点,AB=AC=12米,BC=10米,
∴EF=12BC=5(米),BE=12AB=6(米),CF=12AB=6(米),
∴需要篱笆的长=5+6+6+10=27(米),
故选:C.
根据三角形中位线定理求出EF,根据三角形的中点的概念分别求出BE、CF,计算即可.
本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
9.【答案】D
【解析】解:∵AD⊥BC,BD=9,csB=35,
∴AB=BDcsB=15,
∴AD= AB2−BD2=12,
∵DC=5,
∴AC= AD2+DC2=13,
∵E为边AC的中点,
∴ED=12AC=EA,
∴∠ADE=∠DAE,
∴cs∠ADE=cs∠DAE=ADAC=1213,
故选:D.
根据勾股定理以及余弦值可得AD=12,再由勾股定理可得AC=13,根据直角三角形中斜边上中线等于斜边的一半,可得ED=12AC=EA,由等边对等角可得∠ADE=∠DAE,由此计算角的余弦即可.
本题考查了勾股定理,锐角三角函数解三角形,等腰三角形的判定与性质,利用转化的思想是解题的关键.
10.【答案】C
【解析】解:∵开口向下,
∴a<0,
∵抛物线和y轴的正半轴相交,
∴c>0,
∵对称轴为x=−b2a=−1,
∴b=2a<0,
∴abc>0,故①正确;
当x=1时,y<0,则a+b+c<0,
∴a+b<−c,故②正确;
由图象可知,当x=−2时,y>0,
∴4a−2b+c>0,故③正确;
∵当x=1时,a+b+c<0,b=2a,
∴a=12b,
∴12b+b+c<0,
∴3b+2c<0,故④正确;
∵当x=−1时,二次函数有最大值,
所以当m为任意实数时,有a−b+c≥am2+bm+c,
所以a−b≥m(am+b),故⑤错误.
故选:C.
根据抛物线开口方向,对称轴以及与y轴的交点即可判断①;根据x=1时,y<0即可判断②;根据当x=−2时,y>0,即可判断③;由2a=b,结合当x=1时,a+b+c<0即可判断④;根据x=−1时,函数y=a−b+c的值最大,即可判断⑤.
本题主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换的熟练运用.
11.【答案】95
【解析】解:∵xy=45,
∴可以假设x=4k,y=5k,
∴x+yy=4k+5k5k=95,
故答案为:95.
设x=4k,y=5k,代入式子化简求解即可.
本题考查比例的性质,解题的关键是掌握比例的性质.
12.【答案】13
【解析】解:由图形知:tan∠ACB=26=13,
故答案为:13.
结合图形,根据锐角三角函数的定义即可求解.
题考查了锐角三角函数的定义,属于基础题,关键是掌握锐角三角函数的定义.
13.【答案】14
【解析】解:设雄奇险秀的铜山为A、驻马店市山峰之最的白云山为B、中原盘古圣地盘古山为C,默默无闻的弥勒佛祖道场罗汉山为D,根据题意画出树状图,如图所示:
∵有16种等可能的情况数,其中两人恰好选择同一景点的情况数有4种,
∴两人恰好选择同一景点的概率是:416=14,
故答案为:14.
先根据题意画出树状图,然后根据概率公式进行计算即可.
本题主要考查了用树状图或列表法求等可能事件的概率,方法是用树状图或列表法列举出所有可能出现的结果总数,找出符合条件的结果数,用分数表示即可,注意每种情况发生的可能性相等.
14.【答案】334
【解析】解:∵抛物线y=ax2+bx+c的顶点为P(−2,2),
∴y=a(x+2)2+2,
∵与y轴交于点A(0,3),
∴3=a(0+2)2+2,解得a=14,
∴原抛物线的解析式为:y=14(x+2)2+2,
∵平移该抛物线使其顶点P由(−2,2)移动到P(1,−1),
∴平移后的抛物线为y=14(x−1)2−1,
∴当x=0时,y=−34,
∴A′的坐标为(0,−34),
∴AA′的长度为:3−(−34)=334.
故答案为:334.
先运用待定系数法求出原抛物线的解析式,再根据平移不改变二次项系数,得出平移后的抛物线解析式,求出A′的坐标,进而得出AA′的长度.
本题考查了运用待定系数法求抛物线的解析式,图象平移的规律,二次函数图象上点的坐标特征,难度适中.
15.【答案】2
【解析】解:取AB的中点M,连结MP,MD,PD,如图所示:
∵ABAD=64=32,AEDF=32,
∴ABAD=AEDF,
∵∠BAD=∠ADF=90°,
∴△BAD~△ADF,
∴∠ABE=∠DAF,
∴∠APB=∠DAF+∠AEB=∠ABE+∠AEB=90°,
∵M是AB的中点,
∴MP=12AB=3,
在Rt△MPD中,MD= MA2+AD2=5,
∵∠APB=90°,
∴点P在以AB为直径的⊙M上,
∴PD≤MD−MP,
∴当M,P,D在同一直线上时,DP最小,
DP的最小值为:MD−MP=5−3=2,
故答案为:2.
通过证明相似得出∠APB=90°,再确定点P是在以AB为直径的⊙M上,进而确定当M,P,D在同一直线上时,DP最小,再用直角三角形的性质和勾股定理求解即可.
本题考查了相似三角形的判定和性质,圆周角定理的推论,矩形的性质和直角三角形的性质,确定点P在以AB为直径的⊙M上是解题的关键.
16.【答案】解:(1)原式=3−1−3 3+6× 33
=3−1−3 3+2 3
=2− 3;
(2)原式=12×1+( 32)2−2×12
=12+34−1
=14.
【解析】(1)根据平方差公式进行运算,同时将二次根式化为最简二次根式,再进行实数加减运算,即可求解;
(2)先将特殊角的三角函数值代入式子,再进行实数混合运算,即可求解.
本题主要考查了二次根式混合运算,特殊角三角函数值的混合运算,实数混合运算,掌握二次根式化简方法及特殊角三角函数值是解题的关键.
17.【答案】解:(1)本次调查的学生总人数为(2+4)÷30%=20人,
则B项目中女生人数为20×25%−3=2,E组男生有20−(2+5+6+4+2)=1人,
补全图形如下:
(2)A组所对的扇形圆心角的度数为360°×220=36°;
(3)画树状图如下:
由树状图知共有12种等可能结果,其中恰好抽到两位女学生的有2种结果,
所以恰好抽到两位女学生的概率为212=16.
【解析】(1)由C组所占的百分比和C组有6人即可求得总人数,然后求得B组的女生数和E组的男生数,从而补全条形统计图;
(2)用360°乘A组人数所占比例可得;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与所抽的两位学生恰好是两位女生的情况,再利用概率公式求解即可求得答案.
此题考查了列表法或树状图法求概率,条形统计图,扇形统计图.注意概率=所求情况数与总情况数之比.
18.【答案】解:(1)证明:∵△=(m+3)2−4(m+2)
=(m+1)2,
∵无论m取何值,(m+1)2≥0,
∴原方程总有两个实数根.
(2)∵x1,x2是原方程的两根,
∴x1+x2=−(m+3),x1x2=m+2,
∵x12+x22=2,
∴(x1+x2)2−2x1x2=2,
∴代入化简可得:m2+4m+3=0,
解得:m=−3或m=−1
【解析】(1)根据根的判别式即可求出答案.
本题考查根与系数的关系,解题的关键是熟练运用根与系数的关系,本题属于基础题型.
19.【答案】解:作AN⊥CM于点N.则四边形ABMN是矩形,AN=BM=15(米).
在直角△ANC中,tan∠CAN=CNAN,
则CN=AN⋅tan∠CAN=15⋅tan45°=15×1=15(米).
同理,DN=AN⋅tan∠DAN=15⋅tan37.3°=15×0.7618=11.427(米).
则CD=CN−DN=15−11.427=3.573≈3.6(米).
答:这个广告牌高3.6米.
【解析】作AN⊥CM于点N.则四边形ABMN是矩形,AN=BM,在直角△ANC和直角△AND中,利用三角函数求的CN和DN,根据CD=CN−DN即可求解.
本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.
20.【答案】解:(1)∵每平方米种植的株数每增加1株,单株产量减少0.5千克,
∴y=4−0.5(x−2)=−0.5x+5,
答:y关于x的函数表达式为y=−0.5x+5,(2≤x≤8,且x为整数);
(2)设每平方米小番茄产量为W千克,
根据题意得:W=x(−0.5x+5)=−0.5x2+5x=−0.5(x−5)2+12.5,
∵−0.5<0,
∴当x=5时,W取最大值,最大值为12.5,
答:每平方米种植5株时,能获得最大的产量,最大产量为12.5千克.
【解析】(1)由每平方米种植的株数每增加1株,单株产量减少0.5千克,即可得y=4−0.5(x−2)=−0.5x+5,
(2)设每平方米小番茄产量为W千克,由产量=每平方米种植株数×单株产量即可列函数关系式,由二次函数性质可得答案.
本题考查二次函数的应用,解题的关键是读懂题意,列出函数关系式.
21.【答案】解:(1)由题可知:抛物线的顶点为(8,5),
设水流形成的抛物线为y=a(x−8)2+5,
将点(0,1)代入可得a=−116,
∴抛物线为:y=−116(x−8)2+5.
(2)能,理由如下:
当x=12时,y=−116(12−8)2+5=4>3.5,
∴水流不能碰到这棵果树.
【解析】(1)设抛物线的解析式为y=a(x−8)2+5,用待定系数法求得解析式;
(2)将x=12代入(1)中所求代数式,再跟3.5进行比较.
本题考查了二次函数在实际问题中的应用,正确理解题意、熟练掌握待定系数法及二次函数的性质是解题的关键.
22.【答案】(1)证明:∵OD//BC,
∴∠ODB=∠CBD,
∵OB=OD,
∴∠ODB=∠OBD,
∴∠OBD=∠CBD,
∴BD平分∠ABC;
(2)解:过O点作OH⊥BC于H,
∵BC=4,
∴BH=CH=12BC=2,
∵DE⊥AB,OH⊥BC,
∴∠DEO=90°,∠OHB=90°,
∵OD//BC,
∴∠DOE=∠OBH,
在△ODE和△BOH中,
∠DEO=∠OHB∠DOE=∠OBHOD=OB,
∴△ODE≌△BOH(AAS),
∴DE=OH=3,
在Rt△OBH中,OB= BH2+OH2= 22+32= 13,
即⊙O的半径长为 13.
【解析】(1)利用平行线的性质得到∠ODB=∠CBD,根据半径相等可得∠ODB=∠OBD,等量代换得到∠OBD=∠CBD,进而证得结论;
(2)过O点作OH⊥BC于H,如图,根据垂径定理得到BH=CH=2,再证明△ODE≌△BOH得到DE=OH=3,然后利用勾股定理计算OB的长即可.
本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理和全等三角形的判定与性质.
23.【答案】(1)AEDE;
(2)∵∠B=∠ADE=∠C,∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC,
∴∠EDC=∠BAD,
∵DA=DE,
在△ADB与△DEC中,
∠B=∠C∠BAD=∠EDCDA=DE,
∴△ADB≌△DEC(AAS),
∴EC=BD,AB=DC=b,
∴BD=BC−DC=a−b,
即CE=a−b;
(3)∵∠DEF=∠B,
∴∠BFE+∠BEF=∠BEF+∠DEC,
∴∠BFE=∠DEC,
作CG//FE交DE于点G,如图:
∴∠DEF=∠EGC,
∴∠B=∠EGC,
∴△FBE∽△EGC,
∴BEFE=CGEC,
∵四边形ABCD是平行四边形,
∴∠B+∠BCD=180°,
∵∠EGC+∠DGC=180°,
∵∠B=∠EGC,
∴∠DGC=∠BCD,
∵∠EDC=∠CDG,
∴△DGC∽△DCE,
∴DCDE=CGEC,
∴BEFE=DCDE,
∴DC⋅FE=BE⋅DE,
∵四边形ABCD是平行四边形,
∴AB=DC,
∴AB⋅FE=⋅BE⋅DE.
【解析】(1)解:∵△ABC∽△DAE,
∴BCAC=AEDE,
故答案为:AEDE;
(2)解:∵∠B=∠ADE=∠C,∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC,
∴∠EDC=∠BAD,
∵DA=DE,
在△ADB与△DEC中,
∠B=∠C∠BAD=∠EDCDA=DE,
∴△ADB≌△DEC(AAS),
∴EC=BD,AB=DC=b,
∴BD=BC−DC=a−b,
即CE=a−b;
(3)解:∵∠DEF=∠B,
∴∠BFE+∠BEF=∠BEF+∠DEC,
∴∠BFE=∠DEC,
作CG//FE交DE于点G,如图:
∴∠DEF=∠EGC,
∴∠B=∠EGC,
∴△FBE∽△EGC,
∴BEFE=CGEC,
∵四边形ABCD是平行四边形,
∴∠B+∠BCD=180°,
∵∠EGC+∠DGC=180°,
∵∠B=∠EGC,
∴∠DGC=∠BCD,
∵∠EDC=∠CDG,
∴△DGC∽△DCE,
∴DCDE=CGEC,
∴BEFE=DCDE,
∴DC⋅FE=BE⋅DE,
∵四边形ABCD是平行四边形,
∴AB=DC,
∴AB⋅FE=⋅BE⋅DE.
(1)根据相似三角形的性质即可求得结果;
(2)由已知易证△ADB≌△DEC,进而利用全等三角形的性质即可求出CE的长度;
(3)作CG//FE交DE于点G.易证△FBE∽△EGC,利用相似三角形的性质解答即可.
此题考查相似三角形的综合题,关键是根据相似三角形的判定和性质,全等三角形的判定和性质,平行四边形的性质解答.
2022-2023学年河南省驻马店市泌阳县七年级(下)月考数学试卷(5月份)(含解析): 这是一份2022-2023学年河南省驻马店市泌阳县七年级(下)月考数学试卷(5月份)(含解析),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年河南省驻马店市泌阳县八年级(下)期末数学试卷(含解析): 这是一份2022-2023学年河南省驻马店市泌阳县八年级(下)期末数学试卷(含解析),共24页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2022-2023学年河南省驻马店市泌阳县七年级(下)期末数学试卷(含解析): 这是一份2022-2023学年河南省驻马店市泌阳县七年级(下)期末数学试卷(含解析),共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













