2018年辽宁省营口市中考数学真题及答案

这是一份2018年辽宁省营口市中考数学真题及答案，共15页。试卷主要包含了填空题（每小题3分,共24分)，解答题（本题满分14分)等内容，欢迎下载使用。

一、选择题（下列各题的备选答案中,只有一个是正确的,每小题3分,共30分)
1．3的倒数是（ C ）
A．﹣3 B．﹣ C． D．3
2．如图1，该几何体是由5个棱长为1个单位长度的正方体摆放而成，将正方体A向右平移2个单位长度后（如图2），所得几何体的视图（ D ）
A．主视图改变，俯视图改变 B．主视图不变，俯视图不变
C．主视图改变，俯视图不变 D．主视图不变，俯视图改变
3．下列运算中，正确的是（ B ）
A．x3•x3＝x9 B．3x2+2x2＝5x2 C．（x2）3＝x5 D．（x+y）2＝x2+y2
4．若一组数据1，2，x，4的平均数是2，则这组数据的众数为（ A ）
A．1 B．2 C．3 D．4
5．关于x的一元二次方程x2﹣x+m＝0有两个不相等的实数根，则实数m的取值范围是（ C ）
A．m＞ B．m＝ C．m＜ D．m≤
6．如图，在△ABC中，AB＝AC，∠BAC＝100°，在同一平面内，将△ABC绕点A顺时针旋转到△AB1C1的位置，连接BB1，若BB1∥AC1，则∠CAC1的度数是（ B ）
A．10° B．20° C．30° D．40°
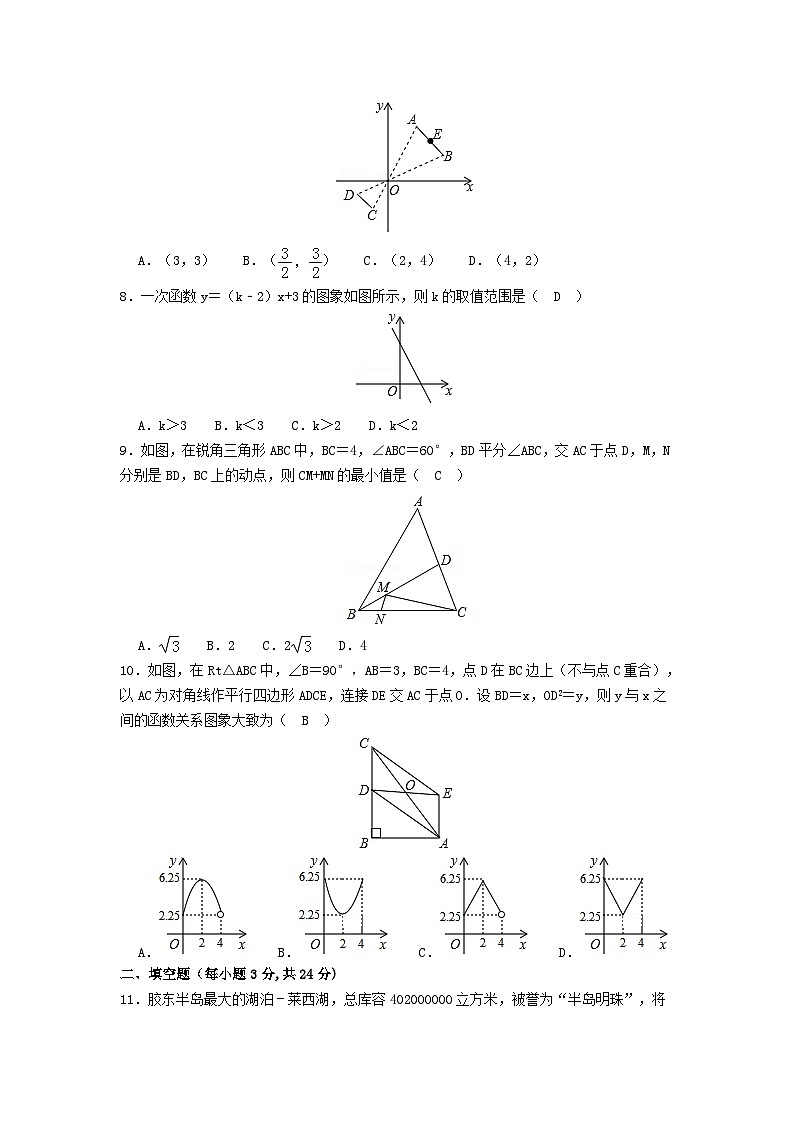
7．如图，线段CD两个端点的坐标分别为C（﹣1，﹣2），D（﹣2，﹣1），以原点O为位似中心，在第一象限内将线段CD扩大为原来的2倍，得到线段AB，则线段AB的中点E的坐标为（ A ）
A．（3，3） B．（） C．（2，4） D．（4，2）
8．一次函数y＝（k﹣2）x+3的图象如图所示，则k的取值范围是（ D ）
A．k＞3 B．k＜3 C．k＞2 D．k＜2
9．如图，在锐角三角形ABC中，BC＝4，∠ABC＝60°，BD平分∠ABC，交AC于点D，M，N分别是BD，BC上的动点，则CM+MN的最小值是（ C ）
A． B．2 C．2 D．4
10．如图，在Rt△ABC中，∠B＝90°，AB＝3，BC＝4，点D在BC边上（不与点C重合），以AC为对角线作平行四边形ADCE，连接DE交AC于点O．设BD＝x，OD2＝y，则y与x之间的函数关系图象大致为（ B ）
A． B． C． D．
二、填空题（每小题3分,共24分)
11．胶东半岛最大的湖泊﹣莱西湖，总库容402000000立方米，被誉为“半岛明珠”，将402000000用科学记数法表示为 ．
【解答过程】解：将402000000用科学记数法表示为4.02×108．
故答案是：4.02×108．
12．函数y＝中，自变量x的取值范围是 ．
【解答过程】解：根据题意得：，
解得：x≥1且x≠2．
故答案为：x≥1且x≠2．
13．在一个不透明的小盒中装有m张除颜色外其它完全相同的卡片，这m张卡片中两面均为红色的只有3张．搅匀后，从小盒中任意抽出一张卡片记下颜色，再放回小盒中．通过大量重复抽取卡片实验，发现抽到两面均为红色卡片的频率稳定在0.3附近，可推算出m的值约为 ．
【解答过程】解：由题意可得，＝0.3，
解得，m＝10．
故答案为：10．
14．如图，点A是反比例函数y＝（x＞0）的图象上任意一点，AB∥x轴交反比例函数y＝（k≠0）的图象于点B，以AB为边作平行四边形ABCD，点C，点D在x轴上．若S▱ABCD＝5，则k＝ ．
【解答过程】解：设点A（x，），则B（，），
∴AB＝x﹣，
则（x﹣）＝5，
k＝﹣3．
故答案为：﹣3．
15．如图1，OC是⊙O的半径，弦AB垂直平分OC，垂足为点D，AB＝6cm，连接OA，OB，将图中阴影部分的扇形OAB剪下围成一个圆锥的侧面（如图2），则圆锥的底面圆半径是 ．
【解答过程】解：∵弦AB垂直平分OC，
∴OA＝OC＝2OD，
则∠OAD＝30°，∠AOC＝60°，
∴∠AOB＝120°，
∵AB＝6cm，
∴AD＝3cm，
则OA＝＝＝6（cm），
∴扇形的弧长，即圆锥的底面周长为＝4π，
则2πr＝4π，
解得r＝2，
故答案为：2cm．
16．“满意“超市对某瓶装饮料进行打折促销，每瓶比原价便宜了0.6元，已知打折后用20元购买的瓶数和打折前用26元购买的瓶数相等．若设该饮料原价每瓶x元，则根据题意可列出分式方程为 ．
【解答过程】解：设该饮料原价每瓶x元，则打折后每瓶（x﹣0.6）元，
依题意，得：＝．
故答案为：＝．
17．如图，在矩形ABCD中，AD＝8，AB＝4，将矩形ABCD折叠，使点A与点C重合，折痕为MN．给出以下四个结论：①△CDM≌△CEN；②△CMN是等边三角形；③CM＝5；④BN＝3．其中正确的结论序号是 ．
【解答过程】解：∵四边形ABCD是矩形
∴AD∥BC，AD＝BC＝8，AB＝CD＝4，
∴∠AMN＝∠MNC，
∵折叠
∴AB＝CE＝4，∠AMN＝∠NMC，AM＝CM
∴∠MNC＝∠CMN，
∴CM＝CN，且CE＝CD
∴Rt△CDM≌Rt△CEN（HL）
∴CN＝CM，
∵MC2＝MD2+CD2，
∴MC2＝（8﹣MC）2+16，
∴MC＝5，
∴CN＝5，
∴BN＝BC﹣CN＝3
故①③④正确
∵MD＝AD﹣AM＝3，且MC＝5，
∴MD≠MC，即∠MCD≠30°
∴∠MCN≠60°
∴△CMN不是等边三角形
故②错误
故答案为①③④
18．如图，在平面直角坐标系中，点A在第一象限，点B在y轴的正半轴上，△AOB为等边三角形．射线OP⊥AB，在射线OP上依次取点P1，P2，P3，…，Pn，使OP1＝1，P1P2＝2，P2P3＝4，…，Pn﹣1Pn＝2n﹣1（n为正整数，点P0即为原点O）分别过点P1，P2，P3，…，Pn向y轴作垂线段，垂足分别为点H1，H2，H3，…，Hn，则点Hn的坐标为 ．
【解答过程】解：∵△OAB是等边三角形，
∴∠AOB＝60°，
∵OP⊥AB，
∴∠BOP＝30°，
∵PnHn⊥y轴，
∴OHn＝OPn，
∵OP1＝1，P1P2＝2，P2P3＝4，…，Pn﹣1Pn＝2n﹣1（n为正整数，）
∴OPn＝1+2+22+23+…+2n﹣1，
∴2OPn＝2+22+23+…+2n﹣1+2n，
∴2OPn﹣OPn＝2n﹣1，
∴OPn＝2n﹣1，
∴OHn＝（2n﹣1）＝2n﹣1﹣，
∴Hn（0，2n﹣1﹣），
故答案为：（0，2n﹣1﹣），
三、解答题（19小题10分,20小题10分,共20分)
19．（10分）先化简，再求值：÷（x+2），其中x＝﹣2﹣1．
【解答过程】解：原式＝÷（﹣）
＝÷
＝•
＝
＝，
当x＝﹣2﹣1＝﹣2时，
原式＝＝＝．
20．（10分）在创建“文明校园”活动中，某校有2名男生和3名女生被评为学校“文明学生”．现要从这5名学生中选拔“学校文明礼仪值周岗”的值周生．
（1）从这5名学生中随机选拔1人值周，恰好选到男生的概率是 ．
（2）从这5名学生中随机选拔2人值周，请用树状图或列表法求出恰好选到1个男生和1个女生的概率．
【解答过程】解：（1）∵有2名男生和3名女生，共5名学生，
∴恰好选到男生的概率是；
故答案为：；
（2）根据题意画树状图如下：
共有20种等情况数，其中选到1个男生和1个女生的有12种情况，
则恰好选到1个男生和1个女生的概率是＝．
四、解答题（21小题12分,22小题12分,共24分)
21．（12分）为加强未成年人思想道德建设．某校在学生中开展了“日行一孝”活动．活动设置了四个爱心项目：A项﹣我为父母过生日，B项﹣我为父母洗洗脚，C项﹣我当一天小管家，D项﹣我与父母谈谈心，要求每个学生必须且只能选择一项参加．为了解全校参加各项目的学生人数，随机抽取了部分学生进行调查，根据调查结果，绘制成如下两幅不完整的统计图，请根据所给信息，解答下列问题：
（1）这次抽样调查的样本容量是 ，补全图1中的条形统计图．
（2）在图2的扇形统计图中，B项所占的百分比为m%，则m的值为 ，C项所在扇形的圆心角α的度数为 度．
（3）该校参加活动的学生共1200人，请估计该校参加D项的学生有多少人？
【解答过程】解：（1）这次抽样调查的样本容量是（人），B的人数200﹣90﹣60﹣10＝40，
如图所示：
（2）B项所占的百分比为m%，则m%的值为，C项所在扇形的圆心角α的度数为360°×45%＝162°；
（3）1200人参加D项的学生的人数为（人）；
故答案为：200；20；162．
22．（12分）如图，建筑物AB的高为52米，在其正前方广场上有人进行航模试飞．从建筑物顶端A处测得航模C的俯角α＝30°，同一时刻从建筑物的底端B处测得航模C的仰角β＝45°，求此时航模C的飞行高度．（精确到1米）
（参考数据：≈1.41，≈1.73，≈2.45）
【解答过程】解：如图，过点C作CD⊥AB于点D，
则∠ACD＝30°，∠BCD＝45°，
设AD＝x，
在Rt△ACD中，CD＝＝＝x，
在Rt△BCD中，由∠BCD＝45°知BD＝CD＝x，
∴由AD+BD＝AB得x+x＝52，
解得：x＝26（﹣1）＝26﹣26，
则BD＝x＝78﹣26≈33，
答：此时航模C的飞行高度为33米．
五、解答题（23小题12分,24小题12分,共24分)
23．（12分）如图，△ABC内接于⊙O，AB是⊙O的直径，弦CD与AB交于点E，连接AD，过点A作直线MN，使∠MAC＝∠ADC．
（1）求证：直线MN是⊙O的切线．
（2）若sin∠ADC＝，AB＝8，AE＝3，求DE的长．
【解答过程】（1）证明：∵AB是⊙O的直径，
∴∠ACB＝90°，
∴∠B+∠BAC＝90°，
∵∠B＝∠D，∠MAC＝∠ADC，
∴∠B＝∠MAC，
∴∠MAC+∠CAB＝90°，
∴∠BAM＝90°，
∴AB⊥MN，
∴直线MN是⊙O的切线；
（2）解：连接OC，过E作EH⊥OC于H，
∵sin∠ADC＝，
∴∠D＝30°，
∴∠B＝∠D＝30°，
∴∠AOC＝60°，
∵AB＝8，
∴AO＝BO＝4，
∵AE＝3，
∴OE＝1，BE＝5，
∵∠EHO＝90°，
∴OH＝，EH＝，
∴CH＝，
∴CE＝＝，
∵弦CD与AB交于点E，
由相交弦定理得，AE•BE＝CE•DE，
∴DE＝＝＝．
24．（12分）某商场销售A，B两款书包，已知A，B两款书包的进货价格分别为每个30元，50元，商场用3600元的资金购进A，B两款书包共100个．
（1）求A，B两款书包分别购进多少个．
（2）市场调查发现，B款书包每天的销售量y（个）与销售单价x（元）有如下关系：y＝﹣x+90（60≤x≤90）．设B款书包每天的销售利润为w元，当B款书包的销售单价为多少元时，商场每天B款书包的销售利润最大？最大利润是多少元？
【解答过程】解：（1）设购进A款书包x个，则B款为100﹣x个，
由题意得：30x+50（100﹣x）＝3600，
解得：x＝70，
即：A，B两款书包分别购进70和30个；
（2）由题意得：w＝y（x﹣50）＝﹣（x﹣50）（x﹣90），
∵﹣1＜0，故w有最大值，
函数的对称轴为：x＝70，而60≤x≤90，
故：当x＝70时，w有最大值为400，
即：B款书包的销售单价为70元时B款书包的销售利润最大，最大利润是400元．
六、解答题（本题满分14分)
25．（14分）已知：在△ABC中，∠ACB＝90°，点D是AC边上一点，连接BD，点E是线段BD延长线上一点，连接AE，CE，使∠CAE＝∠CBE，过点C作CF⊥CE，交BD于点F．
（1）①如图1，当∠ABC＝45°时，线段AE与BF之间的数量关系是 ．
②如图2，当∠ABC＝60°时，线段AE与BF之间的数量关系是 ．
（2）如图3，当∠ABC＝30°时，线段AE与BF之间具有怎样的数量关系？请说明理由．
（3）如图4，当∠ABC＝α（0°＜α＜90°）时，直接写出线段AE与BF之间的数量关系．（用含α的式子表示）
【解答过程】解：（1）①如图1中，结论：AE＝BF．
理由：∵∠BCA＝∠FCE＝90°，
∴∠BCF＝∠ACE，
∵∠ABC＝45°，
∴∠ABC＝∠CAB＝45°，
∴CB＝CA，
∵∠CAE＝∠CBF，
∴△BCF≌△ACE（ASA），
∴BF＝AE．
故答案为BF＝AE．
②如图2中，结论：AE＝BF．
理由：∵∠BCA＝∠FCE＝90°，
∴∠BCF＝∠ACE，
∵∠CAE＝∠CBF，
∴△BCF∽∠ACE，
∴＝
∵∠ABC＝60°，
∴tan60°＝＝，
∴AE＝BF，
故答案为AE＝BF．
（2）如图3中，结论：AE＝BF．
理由：∵∠BCA＝∠FCE＝90°，
∴∠BCF＝∠ACE，
∵∠CAE＝∠CBF，
∴△BCF∽∠ACE，
∴＝
∵∠ABC＝30°，
∴tan30°＝＝，
∴AE＝BF，
（3）如图4中，结论：AE＝BF•tanα．
理由：∵∠BCA＝∠FCE＝90°，
∴∠BCF＝∠ACE，
∵∠CAE＝∠CBF，
∴△BCF∽∠ACE，
∴＝
∵∠ABC＝α，
∴tanα＝
∴AE＝BF•tanα．
七、解答题（本题满分14分)
26．（14分）已知抛物线y＝ax2+bx+8（a≠0）经过点A（﹣3，﹣7），B（3，5），顶点为点E，抛物线的对称轴与直线AB交于点C．
（1）求直线AB的解析式和抛物线的解析式．
（2）在抛物线上A，E两点之间的部分（不包含A，E两点），是否存在点D，使得S△DAC＝2S△DCE？若存在，求出点D的坐标；若不存在，请说明理由．
（3）若点P在抛物线上，点Q在x轴上，当以点A，E，P，Q为顶点的四边形是平行四边形时，直接写出满足条件的点P的坐标．
【解答过程】解：（1）设直线AB的解析式为y＝kx+m，
把点A（﹣3，﹣7），B（3，5）代入，得，
解得：，
∴直线AB的解析式为y＝2x﹣1，
把点A（﹣3，﹣7），B（3，5）代入抛物线y＝ax2+bx+8（a≠0），
得，解得，
∴抛物线的解析式为y＝﹣x2+2x+8．
（2）∵y＝﹣x2+2x+8＝﹣（x﹣1）2+9，
∴顶点E（1，9），
设点D（m，﹣m2+2m+8），C（1，1），
过点D作y轴的平行线交直线AB于点M，则M（m，2m﹣1），
∵S△DAC＝，
S△DCE＝，
∵S△DAC＝2S△DCE
∴﹣2m2+18＝2（4﹣4m），
解得m＝﹣1或m＝5（舍去），
∴存在点D（﹣1，5），使得S△DAC＝2S△DCE
（3）A（﹣3，﹣7），E（1，9），
设点P（x，y），
当以点A，E，P，Q为顶点的四边形是平行四边形时，分三种情况讨论：
①当AE为对角线时，根据中点坐标公式可得点Q坐标为（﹣2﹣x，2﹣y），
∵点Q在x轴上，
∴y＝2，
当y＝2时，﹣x2+2x+8＝2，
解得或，
∴点P坐标为（，2）或（，2），
②当AP为对角线时，根据中点坐标公式可得点Q坐标为（x﹣4，y﹣16），
∵点Q在x轴上，
∴y＝16，
当y＝16时，﹣x2+2x+8＝16，
方程无解，舍去
③当PE为对角线时，根据中点坐标公式可得点Q坐标为（x+4，y+16），
∵点Q在x轴上，
∴y＝﹣16，
当y＝﹣16时，﹣x2+2x+8＝﹣16，
解得x＝6或x＝﹣4
∴点P坐标为（6，﹣16）或（﹣4，﹣16），
综上所述，点P的坐标为（，2）或（，2）或（6，﹣16）或（﹣4，﹣16）．