考点串讲05 分式【3大考点串讲+17种题型】-八年级上学期数学期末考点大串讲（人教版）课件PPT

这是一份考点串讲05 分式【3大考点串讲+17种题型】-八年级上学期数学期末考点大串讲（人教版）课件PPT，共44页。PPT课件主要包含了分式方程，分式方程的应用，分式的运算及化简求值，分式方程的定义，分式方程的解法，分式的概念，对于分式，B≠0，A0且B≠0，分式的基本性质等内容，欢迎下载使用。

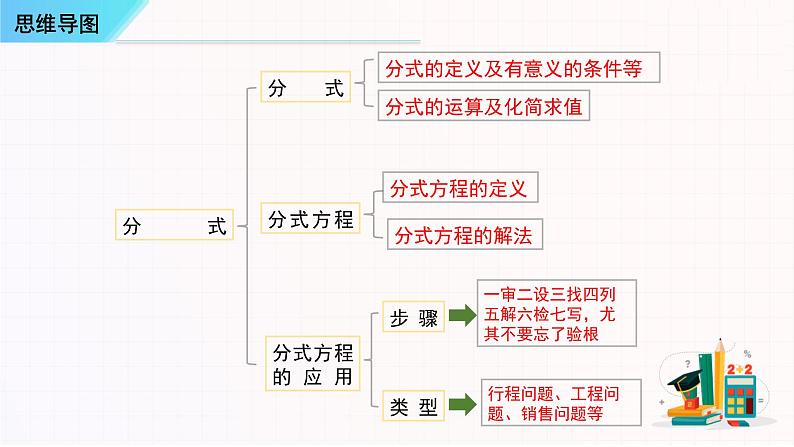
分式的定义及有意义的条件等
一审二设三找四列五解六检七写，尤其不要忘了验根
行程问题、工程问题、销售问题等
2.分式有意义的条件：
当_______时分式有意义；当_______时分式无意义.
3.分式值为零的条件：
根据分式的基本性质，把一个分式的分子与分母的公因式约去，叫做分式的约分．
分子与分母没有公因式的分式，叫做最简分式.
注意：分式的约分，一般要约去分子和分母所有的公因式，使所得的结果成为最简分式或整式.
(1)若分子、分母都是单项式，则约去系数的最大公约数，并约去相同字母的最低次幂；(2)若分子、分母含有多项式，则先将多项式分解因式，然后约去分子、分母所有的公因式．
根据分式的基本性质，把几个异分母的分式分别化成与原来的分式相等的同分母的分式，叫做分式的通分.
为通分要先确定各分式的公分母，一般取各分母的所有因式的最高次幂的积作公分母，它叫做最简公分母.
题型一：能区别分式与整式．
题型二：会确定分式有(或无)意义的条件．
题型三：能熟练对分式进行约分．
题型四：会对分式进行通分．
(1)同分母分式的加减法则：
(2)异分母分式的加减法则：
先算乘方，再算乘除，最后算加减，有括号的先算括号里面的.
计算结果要化为最简分式或整式．
题型五：能熟练进行分式乘法运算．
题型六：能熟练进行分式除法运算．
题型七：能熟练进行分式的乘方运算．
题型八：会进行分式的乘、除、乘方的混合运算．
题型九：能熟练进行同分母分式的加减运算．
题型十：会进行异分母分式的加减法．
题型十一：能熟练进行分式的混合运算．
题型十二：会进行化简求值．
题型十三：会进行整数指数幂的运算．
题型十四：能用科学记数法表示小于1的正数．
分母中含未知数的方程叫做分式方程.
(1)在方程的两边同乘最简公分母，约去分母，化成整式方程.(2)解这个整式方程.(3)把整式方程的解代入最简公分母，如果最简公分母的值不为0，则整式方程的解是原分式方程的解，否则不是，须舍去.
列分式方程解应用题的一般步骤
(1)审:清题意；(2)设:未知数； (3)找:相等关系；(4)列:出方程；(5)解:这个分式方程；(6)验:根（包括两方面 :一是否是分式方程的根； 二是否符合题意）；(7)写:答案.
题型十五：能熟练地解分式方程．
题型十六：理解分式方程的增根．
题型十七：会列分式方程解实际问题．
分式方程中的参数问题
谨防分式运算中的错误
题型五：分式加减时，忽略分数线的作用或漏掉整式项
题型六：求值时，忽略分式有意义的条件