专题5.1 平面向量的概念及其线性运算-2024年高考数学一轮复习《考点•题型 •技巧》精讲与精练

这是一份专题5.1 平面向量的概念及其线性运算-2024年高考数学一轮复习《考点•题型 •技巧》精讲与精练，文件包含专题51平面向量的概念及其线性运算原卷版docx、专题51平面向量的概念及其线性运算解析版docx等2份试卷配套教学资源，其中试卷共41页， 欢迎下载使用。


知识点总结
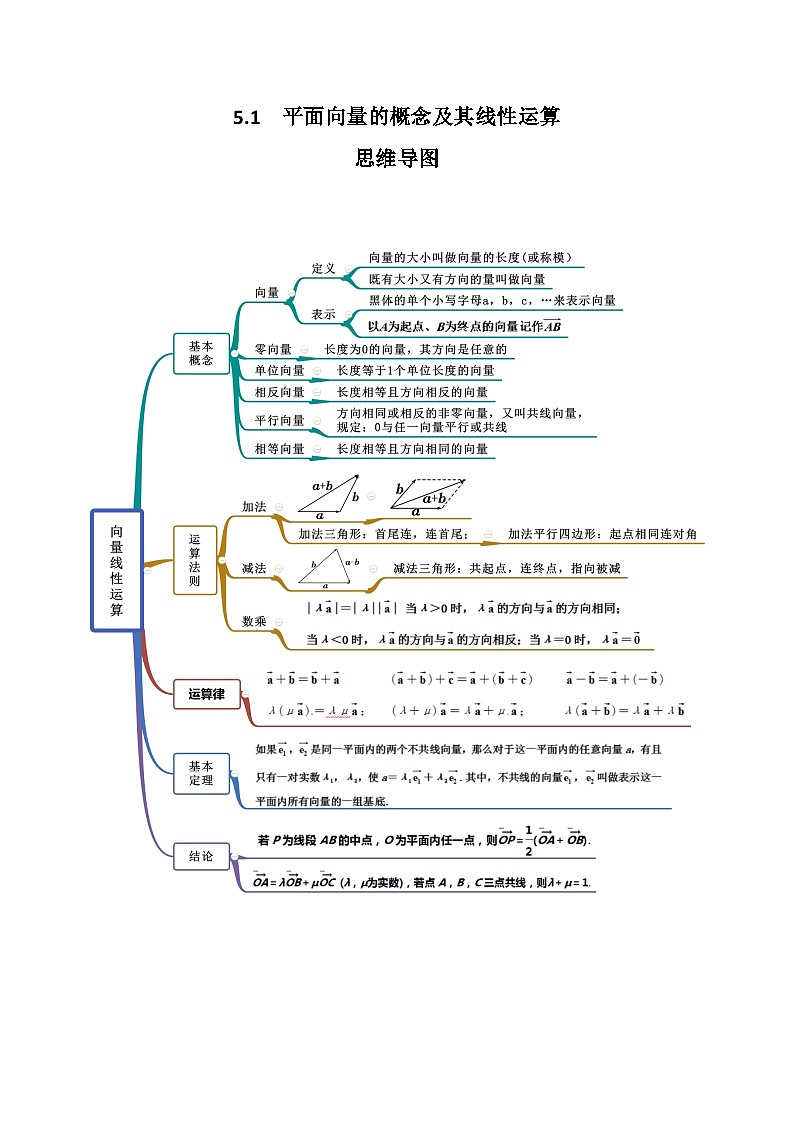
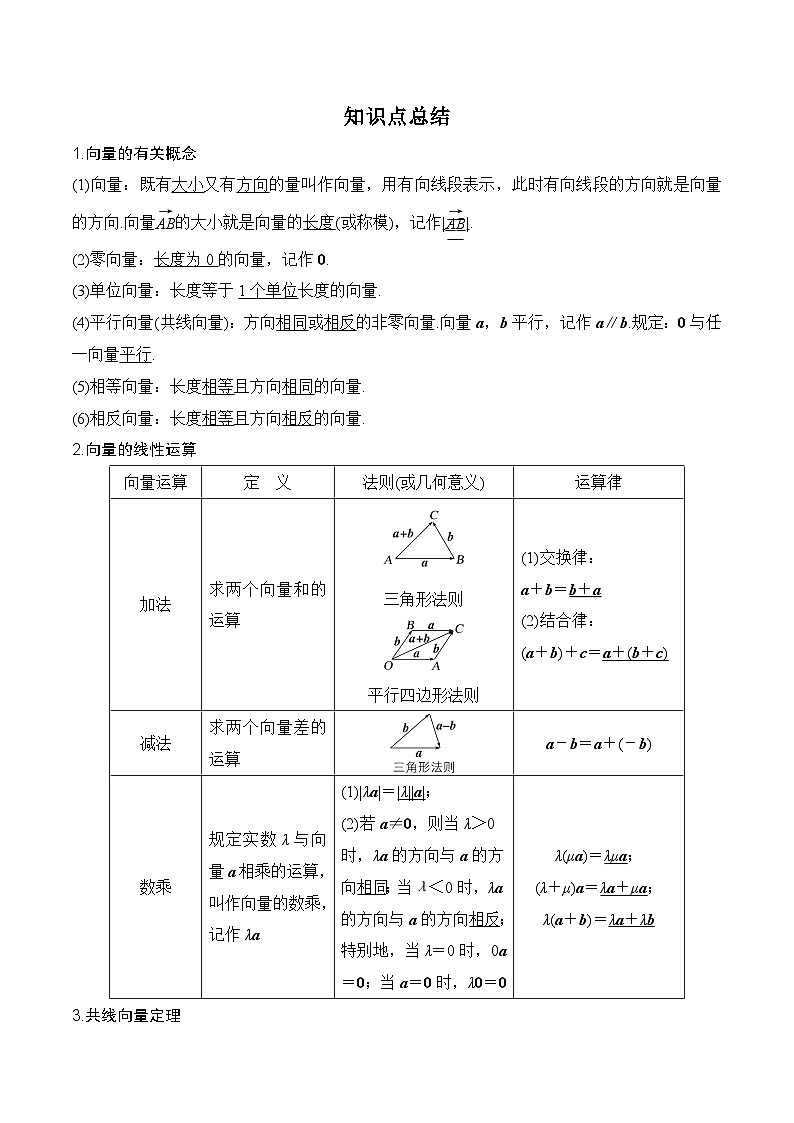
1.向量的有关概念
(1)向量：既有大小又有方向的量叫作向量，用有向线段表示，此时有向线段的方向就是向量的方向.向量eq \(AB,\s\up6(→))的大小就是向量的长度(或称模)，记作 |.
(2)零向量： 的向量，记作0.
(3)单位向量：长度等于 长度的向量.
(4)平行向量(共线向量)：方向相同或相反的非零向量.向量a，b平行，记作a∥b.规定：0与任一向量 .
(5)相等向量：长度 且方向 的向量.
(6)相反向量：长度 且方向 的向量.
2.向量的线性运算
3.共线向量定理
设a为非零向量，如果有一个实数λ，使 ，那么b与a是共线向量；反之，如果b与a是共线向量，那么有且只有一个实数λ，使b＝λa.
[常用结论]
1.中点公式的向量形式：若P为线段AB的中点，O为平面内任一点，则eq \(OP,\s\up6(→))＝eq \f(1,2)(eq \(OA,\s\up6(→))＋eq \(OB,\s\up6(→))).
2.eq \(OA,\s\up6(→))＝λeq \(OB,\s\up6(→))＋μeq \(OC,\s\up6(→))(λ，μ为实数)，若点A，B，C共线(O不在直线BC上)，则λ＋μ＝1.
3.解决向量的概念问题要注意两点：一是不仅要考虑向量的大小，更重要的是考虑向量的方向；二是要特别注意零向量的特殊性，考虑零向量是否也满足条件.
典型例题分析
考向一 平面向量的有关概念
设a，b都是非零向量，下列四个条件中，使eq \f(a,|a|)＝eq \f(b,|b|)成立的充分条件是( )
A.a＝－b B.a∥b
C.a＝2b D.a∥b且|a|＝|b|
感悟提升 平行向量有关概念的四个关注点
(1)相等向量具有传递性，非零向量的平行也具有传递性.
(2)共线向量即为平行向量，它们均与起点无关.
(3)向量可以平移，平移后的向量与原向量是相等向量，解题时，不要把它与函数图象的平移混淆.
考向二 向量的线性运算
角度1 平面向量加、减运算的几何意义
例2 (2023·芜湖调研)如图，等腰梯形ABCD中，AB＝BC＝CD＝3AD，点E为线段CD上靠近C的三等分点，点F为线段BC的中点，则eq \(FE,\s\up6(→))＝( )
A.－eq \f(11,18)eq \(AB,\s\up6(→))＋eq \f(5,18)eq \(AC,\s\up6(→)) B.－eq \f(11,18)eq \(AB,\s\up6(→))＋eq \f(11,9)eq \(AC,\s\up6(→))
C.－eq \f(11,18)eq \(AB,\s\up6(→))＋eq \f(4,9)eq \(AC,\s\up6(→)) D.－eq \f(1,2)eq \(AB,\s\up6(→))＋eq \f(5,6)eq \(AC,\s\up6(→))
角度2 向量的线性运算
例3 在△ABC中，eq \(BD,\s\up6(→))＝eq \f(1,3)eq \(BC,\s\up6(→))，若eq \(AB,\s\up6(→))＝a，eq \(AC,\s\up6(→))＝b，则eq \(AD,\s\up6(→))等于( )
A.eq \f(2,3)a＋eq \f(1,3)b B.eq \f(1,3)a＋eq \f(2,3)b
C.eq \f(1,3)a－eq \f(2,3)b D.eq \f(2,3)a－eq \f(1,3)b
角度3 利用向量的线性运算求参数
例4 在△ABC中，AB＝2，BC＝3eq \r(3)，∠ABC＝30°，AD为BC边上的高.若eq \(AD,\s\up6(→))＝λeq \(AB,\s\up6(→))＋μeq \(AC,\s\up6(→))，则λ－μ＝________.
感悟提升 平面向量线性运算的常见类型及解题策略
(1)向量求和用平行四边形法则或三角形法则；求差用向量减法的几何意义.
(2)求参数问题可以通过向量的运算将向量表示出来，进行比较，求参数的值.
考向三 共线向量定理的应用
例5 (1)(2022·绵阳二诊)已知平面向量a，b不共线，eq \(AB,\s\up6(→))＝4a＋6b，eq \(BC,\s\up6(→))＝－a＋3b，eq \(CD,\s\up6(→))＝a＋3b，则( )
A.A，B，D三点共线 B.A，B，C三点共线
C.B，C，D三点共线 D.A，C，D三点共线
(2)(2023·山西大学附中诊断)如图所示，已知点G是△ABC的重心，过点G作直线分别与AB，AC两边交于M，N两点，设xeq \(AB,\s\up6(→))＝eq \(AM,\s\up6(→))，yeq \(AC,\s\up6(→))＝eq \(AN,\s\up6(→))，则eq \f(1,x)＋eq \f(1,y)的值为( )
A.3 B.4
C.5 D.6
感悟提升 利用共线向量定理解题的策略
(1)a∥b⇔a＝λb(b≠0)是判断两个向量共线的主要依据.注意待定系数法和方程思想的运用.
(2)当两向量共线且有公共点时，才能得出三点共线，即A，B，C三点共线⇔eq \(AB,\s\up6(→))，eq \(AC,\s\up6(→))共线.
(3)若a与b不共线且λa＝μb，则λ＝μ＝0.
(4)eq \(OA,\s\up6(→))＝λeq \(OB,\s\up6(→))＋μeq \(OC,\s\up6(→))(λ，μ为实数)，若A，B，C三点共线(O不在直线BC上)，则λ＋μ＝1.
考向四 等和(高)线定理
(1)由三点共线结论推导等和(高)线定理：如图，由三点共线结论可知，若eq \(OP,\s\up6(→))＝λeq \(OA,\s\up6(→))＋μeq \(OB,\s\up6(→))(λ，μ∈R)，则λ＋μ＝1，由△OAB与△OA′B′相似，必存在一个常数k，k∈R，使得eq \(OP′,\s\up6(→))＝keq \(OP,\s\up6(→))，则eq \(OP′,\s\up6(→))＝keq \(OP,\s\up6(→))＝kλeq \(OA,\s\up6(→))＋kμeq \(OB,\s\up6(→))，又eq \(OP′,\s\up6(→))＝xeq \(OA,\s\up6(→))＋yeq \(OB,\s\up6(→))(x，y∈R)，∴x＋y＝k(λ＋μ)＝k；反之也成立.
(2)平面内一组基底eq \(OA,\s\up6(→))，eq \(OB,\s\up6(→))及任一向量eq \(OP′,\s\up6(→))，eq \(OP′,\s\up6(→))＝λeq \(OA,\s\up6(→))＋μeq \(OB,\s\up6(→))(λ，μ∈R)，若点P′在直线AB上或在平行于AB的直线上，则λ＋μ＝k(定值)；反之也成立，我们把直线AB以及与直线AB平行的直线称为等和(高)线.
例 给定两个长度为1的平面向量eq \(OA,\s\up6(→))和eq \(OB,\s\up6(→))，它们的夹角为120°，如图，点C在以O为圆心的圆弧eq \(AB,\s\up8(︵))上运动，若eq \(OC,\s\up6(→))＝xeq \(OA,\s\up6(→))＋yeq \(OB,\s\up6(→))，其中x，y∈R，则x＋y的最大值是________.
基础题型训练
一、单选题
1．下面给出的关系式中正确的个数是（ ）
①；②；③；④；⑤
A．1B．2C．3D．4
2．下列结论中，正确的是（ ）
A．2 020 cm长的有向线段不可能表示单位向量
B．若O是直线l上的一点，单位长度已选定，则l上有且仅有两个点A，B，使得是单位向量
C．方向为北偏西50°的向量与南偏东50°的向量不可能是平行向量
D．一人从A点向东走500米到达B点，则向量不能表示这个人从A点到B点的位移
3．若＝(1，1)，＝2，且，则与的夹角是（ ）
A．B．C．D．
4．若是边长为1的等边三角形，G是边BC的中点，M为线段AG上任意一点，则的取值范围是（ ）
A．B．C．D．
5．已知向量，在正方形网格中的位置如图所示，那么向量与的夹角为（ ）
A．B．
C．D．
6．已知空间任一点和不共线的三点、、，下列能得到、、、四点共面的是（ ）
A．B．
C．D．以上都不对
二、多选题
7．若是直线l上的一个单位向量，这条直线上的向量，，则下列说法正确的是（ ）
A．B．C．与的夹角为D．
8．对于两个向量和，下列命题中错误的是（ ）
A．若，满足，且与同向，则B．
C．D．
三、填空题
9．若向量，满足，，，则与的夹角为_________.
10．在中，、、分别是角A、、的对边，，，，，则___________.
11．在中，，且，则的最小值是___________.
12．已知向量，，，满足，，，，若，则的最小值为______.
四、解答题
13．运用数量积知识证明下列几何命题：
(1)在中，，则；
(2)在矩形ABCD中，AC＝BD.
14．如图所示，中，，边上的中线交于点，设，用向量表示.
15．已知，且与的夹角为，又，，
(1)求在方向上的投影；
(2)求．
16．平面内给定三个向量，且．
(1)求实数k关于n的表达式；
(2)如图，在中，G为中线OM上一点，且，过点G的直线与边OA，OB分别交于点P，Q（不与重合）.设向量，求的最小值．
提升题型训练
一、单选题
1．已知是互相垂直的单位向量，若，则（ ）
A．B．C．0D．2
2．如图，四边形中，，则相等的向量是（ ）
A．与B．与C．与D．与
3．下列命题正确的是
A．
B．
C．
D．
4．对于非零向量，，定义．若，则（ ）
A．B．C．D．
5．设向量，满足，，，则的取值范围是（ ）
A． [，＋∞)B． [，＋∞)
C．[，6]D．[，6]
6．已知，，则的最大值等于（ ）
A．4B．C．D．5
二、多选题
7．有如下命题，其中真命题为（ ）
A．若幂函数的图象过点，则
B．函数（且）的图象恒过定点
C．函数在上单调递减
D．已知向量与的夹角为，且，，则在方向上的投影向量是．
8．下列命题中假命题的是（ ）
A．向量与向量共线，则存在实数使
B．，为单位向量，其夹角为θ，若，则
C．若，则
D．已知与是互相垂直的单位向量，若向量与的夹角为锐角，则实数k的取值范围是.
三、填空题
9．下列向量中，与一定共线的有_______．（填序号）
①，；
②；；
③，；
④，．
10．已知向量，满足，，且，则与的夹角为______.
11．已知向量与的夹角是，且，则向量与的夹角是_____.
12．已知平行四边形ABCD中，对角线AC，BD相交于点O，已知，则__．
四、解答题
13．如图，网格小正方形的边长均为1，求.
14．如图，按下列要求作答．
(1)以A为始点，作出；
(2)以B为始点，作出；
(3)若为单位向量，求、和．
15．已知，，．
（1）求向量与的夹角；
（2）求
16．如图，设Ox，Oy是平面内相交成角的两条数轴，、分别是x轴，y轴正方向同向的单位向量，若向量，则把有序数对叫做向量在坐标系xOy中的坐标，假设.
(1)计算的大小；
(2)是否存在实数n，使得与向量垂直，若存在，求出n的值，若不存在请说明理由．
向量运算
定 义
法则(或几何意义)
运算律
加法
求两个向量和的运算
三角形法则
平行四边形法则
(1)交换律：
a＋b＝b＋a
(2)结合律：
(a＋b)＋c＝
减法
求两个向量差的运算
a－b＝a＋(－b)
数乘
规定实数λ与向量a相乘的运算，叫作向量的数乘，记作λa
(1)|λa|＝ ；
(2)若a≠0，则当λ＞0时，λa的方向与a的方向相同；当λ＜0时，λa的方向与a的方向相反；特别地，当λ＝0时，0a＝0；当a＝0时，λ0＝0
λ(μa)＝λμa；
(λ＋μ)a＝ ；
λ(a＋b)＝