辽宁省大连市2023年七年级上学期期末数学试题附答案

这是一份辽宁省大连市2023年七年级上学期期末数学试题附答案，共10页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1．﹣3的相反数是（ ）
A．B．C．D．
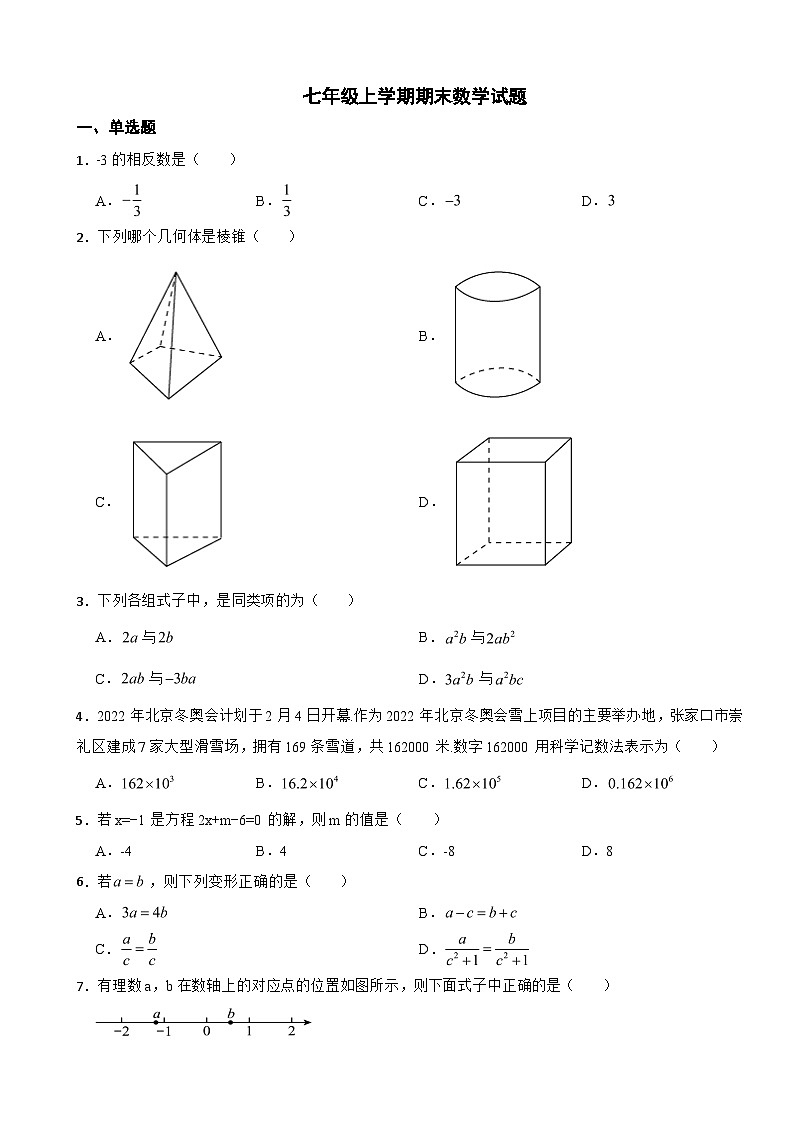
2．下列哪个几何体是棱锥（ ）
A．B．
C．D．
3．下列各组式子中，是同类项的为（ ）
A．与B．与
C．与D．与
4．2022年北京冬奥会计划于2月4日开幕.作为2022年北京冬奥会雪上项目的主要举办地，张家口市崇礼区建成7家大型滑雪场，拥有169条雪道，共162000米.数字162000用科学记数法表示为（ ）
A．B．C．D．
5．若x=−1是方程2x+m−6=0的解，则m的值是（ ）
A．-4B．4C．-8D．8
6．若，则下列变形正确的是（ ）
A．B．
C．D．
7．有理数a，b在数轴上的对应点的位置如图所示，则下面式子中正确的是（ ）
A．B．C．D．
8．如图，货轮O在航行过程中，发现灯塔A在它北偏东的方向上，海岛B在它南偏东方向上．则的度数是（ ）
A．B．C．D．
9．中国古代人民很早就在生产生活中发现了许多有趣的数学问题，其中《孙子算经》中有个问题：今有四人共车，一车空；二人共车，八人步，问人与车各几何？这道题的意思是：今有若干人乘车，每4人乘一车，最终剩余1辆车，若每2人共乘一车，最终剩余8个人无车可乘，问有多少人，多少辆车？如果我们设有x辆车，则可列方程（ ）
A．B．
C．D．
10．如图，从边长为a的大正方形中去掉一个边长为b的小正方形，然后将剩余部分剪后拼成一个长方形，则这个长方形的周长为（ ）
A．B．C．D．
二、填空题
11．数轴上点表示1，从出发沿正方向移动3个单位长度到达点，则点表示的数是 ．
12．若单项式的次数是 .
13．如果代数式x+2y+3的值是0，则代数式2x+4y+5的值是 ．
14．某商店在某时刻以每件60元的价格卖出一件衣服，盈利25%，则这件衣服的进价是 ．
15．比较大小： （填“”，“”或“”）．
16．定义：若，则称a与b是关于2的平衡数．-3与 是关于2的平衡数．
三、解答题
17．如图，已知四点A，B，C，D，请按下列要求画图．
（1）连接；
（2）作射线交直线于点O；
（3）连接，并延长线段至点E，使．
18．计算：
（1）；
（2）．
19．解方程：
（1）；
（2）．
20．先化简求值： ，其中 ， ．
21．某车间有22名工人，每人每天可以生产1200个螺钉或2000螺母，一个螺钉需要配两个螺母，为了使每天生产的螺钉和螺母刚好配套，应安排多少名工人生产螺钉？
22．如图，直线、相交于点O，平分，，．求的度数．
23．观察下列关于x的方程及其解的特征：
的解为；
的解为；
的解为；
…
根据观察得到的规律，解答下列问题：
（1）方程的解为 ；
（2）猜想方程的解，并检证；
（3）直接写出按此规律排列的第2023个方程 ．
24．综合与实践
（1）问题情境：
数学活动课上，王老师出示了一个问题：
如图1，已知线段，点C在线段上，，点P在线段上，．求的长．
请解答王老师提出的问题．
（2）实践探究：
王老师改变条件，并提出新问题，点P在的延长线上时，原题的其他条件不变，求的长．
知识迁移：
数学活动小组同学把上述线段问题改为角研究之后发现，也能提出类似问题．
该小组提出下面的问题，请你解答．
（3）如图3，已知，射线在的内部，，射线在平面内，．请直接写出的度数．
25．科技馆在顺次有A，B，C三点的笔直跑道上，进行机器人行走性能试验．甲、乙两机器人分别从A，B两点按预定程序，同时同向出发，历时同时到达C点．乙机器人始终以的速度行走；甲机器人前匀速运动，在的这段时间，甲、乙两机器人的速度相同，在的这段时间，甲机器人再次匀速运动．甲、乙两机器人之间的距离与他们的行走时间之间的对应的不完整的数据记录如表．请结合表格，回答下列问题：
（1）A，B两点之间的距离是 m， ；
（2）求甲机器人前的速度；
（3）请直接写出在整个运动过程中，两机器人相距时t的值．
1．D
2．A
3．C
4．C
5．D
6．D
7．C
8．B
9．A
10．C
11．4
12．2
13．﹣1
14．48
15．
16．5
17．（1）解：如图，连接
（2）解：如图，作射线交直线于点O．
（3）解：如图，连接，并延长线段至点E，使．
18．（1）解：
；
（2）解：
．
19．（1）解：
去括号，得：
移项，得：
合并同类项，得：
系数化1，得：；
（2）解：
去分母，得：
去括号，得：
移项，得：
合并同类项，得：
系数化1，得：．
20．解：
，
当 ， 时，
原式 ．
21．解：设应安排 人生产螺钉， 人生产螺母.
根据题意得
解得
答：应安排10人生产螺钉.
22．解：，，
，
，
平分，
．
23．（1）
（2）解：方程的解为，
验证：，
去分母，得：，
去括号，得：，
移项合并，得：，
系数化1，得：；
（3）．
24．（1）解：，，，
，
，，
，
，
；
（2）解：，
，
，，，
，
，
；
（3）解：①射线在内，
，，，
，
，，
，
，
；
②射线在外，
，
，
，，，
，
，
．
25．（1）60；30
（2）解：设甲的速度为，
解得∶ ，
甲机器人前的速度是．
（3）解：第一种情况：甲没追上乙之前，
第二种情况：甲追上乙之后，
第三种情况：甲追上乙之后开始减速，
设在的这段时间甲的速度是，
，
解得：，
设设在的这段时间经过时间a，二者差距，
解得：
∴，
综上所述：或2.5或5.5．0
1
2
3
4
5
6
7
60

0
y
y


0