湖北省荆楚初中名校联盟2023-2024学年八年级上学期期中数学试题

这是一份湖北省荆楚初中名校联盟2023-2024学年八年级上学期期中数学试题，共12页。

注意事项：
1.考生答题全部在答题卷上，答在试题卷上无效.
2.请认真核对监考教师在答题卷上所粘贴条形码的姓名、准考证号是否与本人相符，再将自己的姓名、准考证号用0.5毫米的黑色墨水签字笔填写在答题卷及试题卷上.
3.选择题作答必须用2B铅笔将答题卷上对应的答案标号涂黑.如需要改动，请用橡皮擦干净后，再选涂其他答案.非选择题作答必须用0.5毫米黑色墨水签字笔写在答题卷上指定位置，在其他位置答题一律无效.4.考生不得折叠答题卷，保持答题卷的整洁.考试结束后，请将试题卷和答题卷一并上交.
一、选择题（本大题共10个小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的，请将其标号在答题卡上涂黑作答.）
1.在下列“绿色食品、回收、节能、节水”四个标志中，是轴对称图形的是（ ）
A.B.C.D.
2.如图所示，两个三角形全等，则的度数为（ ）
A.41°B.51°C.62°D.77°
3.2022年北京冬奥会开幕式中主火炬台的雪花状创意令人惊叹.如图是一个正六边形雪花状饰品，则它的每一个内角是（ ）
A.60°B.105°C.120°D.135°
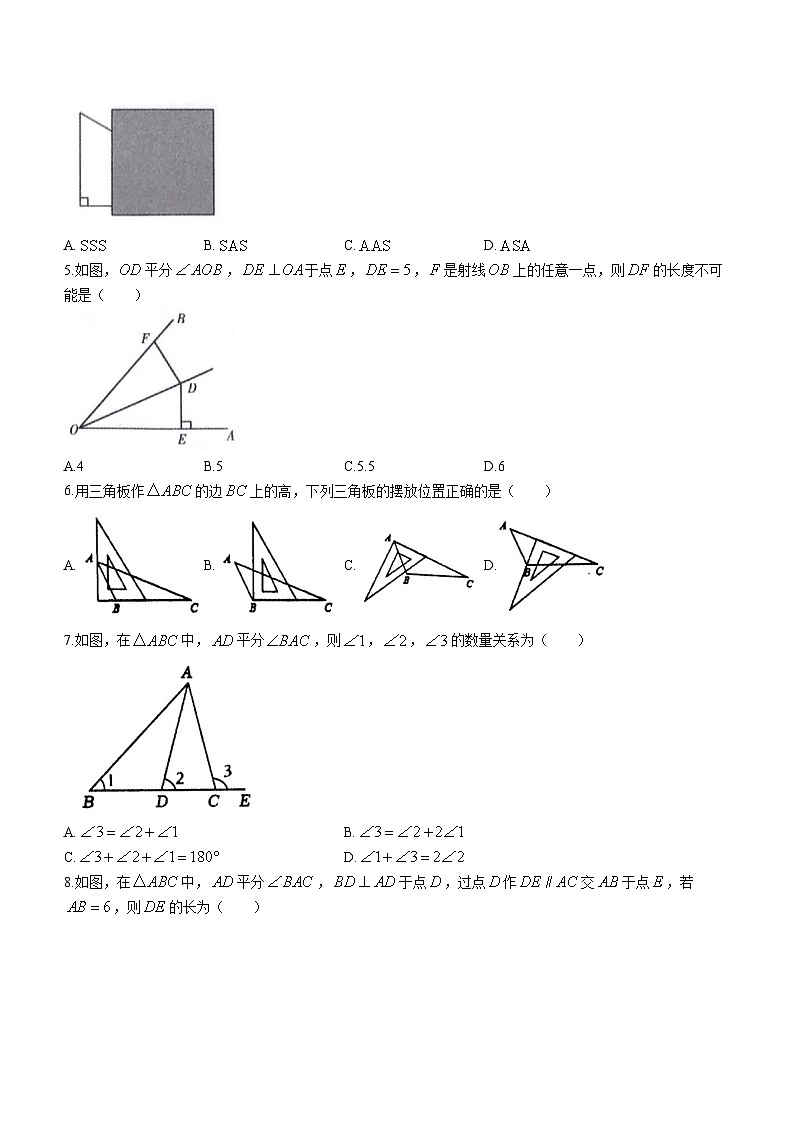
4.如图，直角三角形被挡住了一部分，小芳根据所学知识很快就画出了一个与原来完全一样的三角形，小芳画图的依据是（ ）
A.B.C.D.
5.如图，平分，于点，，是射线上的任意一点，则的长度不可能是（ ）
A.4B.5C.5.5D.6
6.用三角板作的边上的高，下列三角板的摆放位置正确的是（ ）
A.B.C.D.
7.如图，在中，平分，则，，的数量关系为（ ）
A.B.
C.D.
8.如图，在中，平分，于点，过点作交于点，若，则的长为（ ）
A.2.5B.3C.3.5D.4
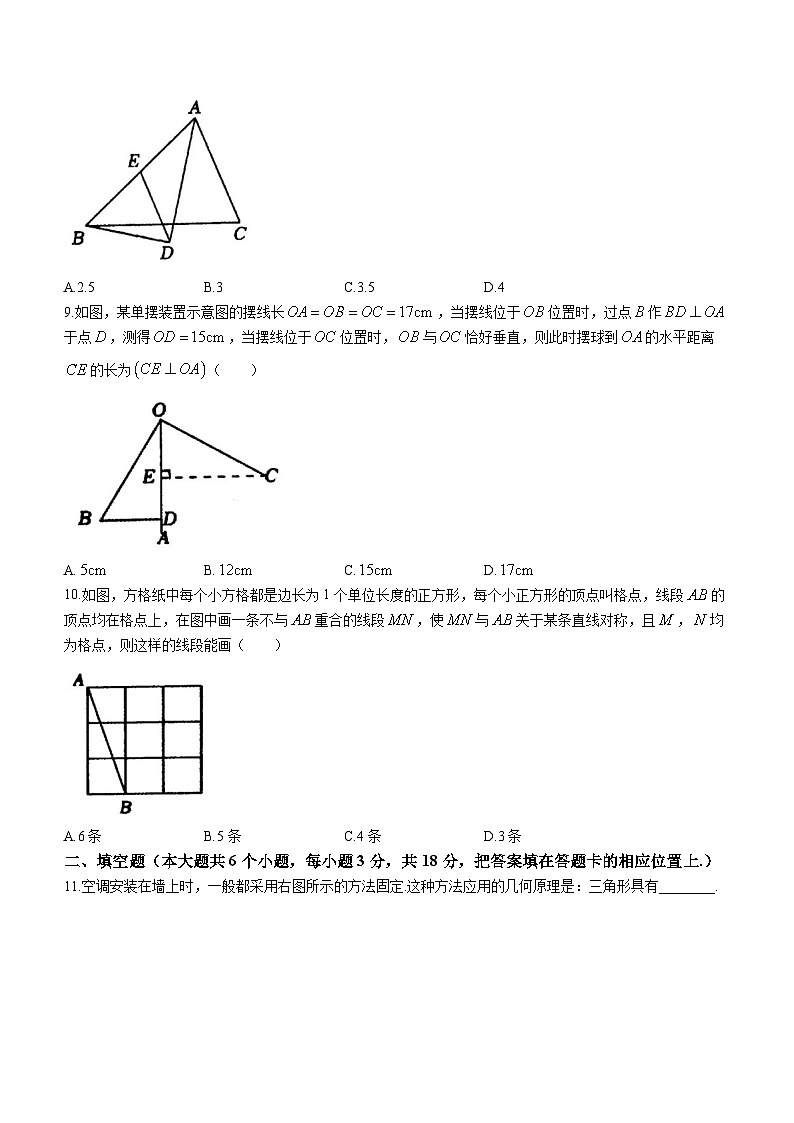
9.如图，某单摆装置示意图的摆线长，当摆线位于位置时，过点作于点，测得，当摆线位于位置时，与恰好垂直，则此时摆球到的水平距离的长为（ ）
A.B.C.D.
10.如图，方格纸中每个小方格都是边长为1个单位长度的正方形，每个小正方形的顶点叫格点，线段的顶点均在格点上，在图中画一条不与重合的线段，使与关于某条直线对称，且，均为格点，则这样的线段能画（ ）
A.6条B.5条C.4条D.3条
二、填空题（本大题共6个小题，每小题3分，共18分，把答案填在答题卡的相应位置上.）
11.空调安装在墙上时，一般都采用右图所示的方法固定.这种方法应用的几何原理是：三角形具有________.
12.某校组织学生进行剪窗花活动，小莉同学将剪好的兔子放在适当的平面直角坐标系中.若兔子两只耳朵上的点与点恰好关于轴对称，则的值为__________.
13.如图，在中，，点是上一点，，的垂直平分线分别交，于点，，则_________度.
14.如图，在中，点是边上一点，且，点在上，连接，，若，，，则_______度.
15.已知，，是的三边，则化简的结果是_________.
16.如图，在和中，，，，，连接，交于点，连接.下列结论：①；②；③平分；④点到和的距离相等.其中正确的有____________（填序号）
三、解答题（本大题共8个小题，共72分.解答应写出文字说明，证明过程或演算步骤，并且写在答题卡上每题对应的答题区域内）
17.（本小题8分）如图，在平面直角坐标系中，各顶点的坐标分别为，，.
（1）作出关于轴对称的图形，并写出顶点的坐标；
（2）求的面积.
18.（本小题8分）学习了《利用三角形全等测距离》后，某同学就“测量河两岸，两点间距离”这一问题，设计了如下方案：如图，在点所在河岸同侧平地上取点和点，使点，，在一条直线上，且，测得，，在的延长线上取一点，使，这时测得的长就是，两点间的距离.你同意他的说法吗?请说明理由.
19.（本小题8分）如图，点在内部，点关于，对称的点分别为，，连接交于点，连接交于点，连接，交于点，交于点，连接，.
（1）若，求的周长；
（2）若，，求的度数.
20.（本小题8分）如图，是直角三角形，，于点，是角平分线，过点作交于点，求证：.
21.（本小题8分）如图所示，已知，分别是的高和中线，，，，.求：
（1）的长；
（2）和的周长的差.
22.（本小题10分）如图，点在边上，，，.
（1）求证：；
（2）若，求的度数.
23.（本小题10分）如图，在中，，分别是，的平分线，，分别是，的平分线.
（1）填空：当，时，__________°，___________°；
（2）当时，求，的度数；
（3）请你猜想，当的大小变化时，的值是否变化?请说明理由.
24.（本小题12分）【问题背景】
如图1，在四边形中，，，，，分别是，上的点，且，试探究图1中线段，，之间的数量关系.
图1 图2
【初步探索】
小卉同学认为：在图1中延长到点，使，连接，先证明，再证明，则可得到，，之间的数量关系是___________.
【探索延伸】
如图2，在四边形中，，，，分别是，上的点，，上述结论是否仍然成立?说明理由.
【结论运用】
如图3，在某次军事演习中，舰艇甲在指挥中心（处）北偏西30°的处，舰艇乙在指挥中心南偏东70°的处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，同时舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后，指挥中心观测到甲、乙两舰艇分别到达，处，且两舰艇之间的夹角为70°，则此时两舰艇之间的距离为____________海里（直接填写结果）.
图3
荆楚初中名校联盟2023-2024年度第一学期期中考试
八年级数学参考答案及评分说明
说明：本评分说明一般只给出一种解法，对其他解法，只要推理严谨，运算合理，结果正确，均给满分；对部分正确的，参照此评分说明，酌情给分.
一、选择题（每小题3分，共30分）
1.A 2.C 3.C 4.D 5.A 6.A 7.D 8.B 9.C 10.B
二、填空题（每小题3分，共18分）
11.稳定性； 12.-5； 13.80 ； 14.40； 15.；
16.①②④（此题得分为1分，2分或3分，答案没写全，写出几个得几分，但若填写有错误序号此题不得分）；
三、解答题（共72分）
17.解：（1）如图，即为所求，点；……………………4分
（2）.…………………………8分
18.解：同意，理由如下： ……………………………………………………1分
∵，，
∴， ……………………2分
∵，
∴， ……………………3分
在和中，
，
∴， ……………………5分
∴， ……………………6分
∵，
∴，即， ……………………7分
∴测得的长就是A，B两点间的距离. ……………………8分
19.解：（1）根据题意点P关于，的对称点分别为C，D，
故有，； ……………………2分
则.
∴的周长=18cm； ……………………4分
（2）根据题意点P关于，的对称点分别为C，D，
∴，， ……………………6分
∵，，
∴， ……………………7分
∴.………8分
20.证明：∵（已知），∴（垂直定义），
∴（直角三角形两锐角互余），
∵（已知），
∴（直角三角形两锐角互余），
∵是的角平分线（已知），
∴（角平分线定义），
∴（等角的余角相等）， ……………4分
∵（对顶角相等），
∴（等量代换）， ……………6分
∵（已知），
∴（ 两直线平行，同位角相等），
∴（ 等量代换）. ……………………8分
21.解：∵，是边上的高，
∴， ……………………2分
∴，
即的长度为4.8cm； …………4分
（2）∵为边上的中线，
∴， ……………………5分
∴和的周长的差为
， ……………………7分
∴和的周长的差是2cm. ……………………8分
22.解：（1）证明：∵，
∴， ……………………1分
∵，，
又∵，
∴， ……………………3分
在与中，
，
∴， …………………………5分
（2）解：∵，
∴，， ……………………8分
∴， ……………………9分
∴. ………………………10分
23.解：（1），； ………………………2分
（2）在中，，
∵，分别是，的平分线，
∴，，
∴
； ……………………4分
∵，分别是，的平分线，
∴
；
∴
； …………6分
（3）的值不变，理由如下： ………………………7分
由（2）可知，，；
.
∴当的大小变化时，的值不变. ………………………10分
24.解：初步探索：. ………………………3分
探索延伸：结论仍然成立，
证明：如图2，延长到G，使，连接， ……………4分
∵，
∴，
在和中，
，
∴，
∴，， ………………………6分
图2
∵，
∴，
∴，
在和中，
，
∴，
∴，
∴； ………………………9分
结论运用：此时两舰艇之间的距离是210海里. ……………12分
【答案如下】如图3，连接，延长，交于点C
图3
∵，，
∴，
∵，
，
∴符合探索延伸中的条件
∴结论成立，
即海里，
答：此时两舰艇之间的距离是210海里.