福建省泉州石狮石光中学、石光三中2023-2024学年九年级上学期期中数学试题

这是一份福建省泉州石狮石光中学、石光三中2023-2024学年九年级上学期期中数学试题，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
考试时长120分钟 总分150分
一、选择题（本大题共10小题，共40分.在每小题列出的选项中，选出符合题目的一项）
1.下列各式：①，②，③，④中，最简二次根式有（ ）
A. 1 个B. 2 个C. 3 个D. 4 个
2.下列方程中，关于的一元二次方程的是（ ）
A.B.C.D.
3.下列等式不成立的是（ ）
A.B.
C.D.
4.若关于的方程有一个根为，则的值为（ ）
A. B.C.2D.4
5.如图，在中，，是边上的中线，是的中位线，若，则的长为（ ）
A.6B.4C.3D.5
6.某阅览室2015年图书借阅总量是7500本，2017年图书借阅总量是10800本.设该阅览室的图书借阅总量从2015年至2017年的年平均增长率为x，则下列方程中，正确的是（ ）
A. B.
C.D.
7.如图，嘉嘉在A时测得一棵4m高的树的影长为8m，若A时和B时两次日照的光线互相垂直，则B时的影长为（ ）
A.2mB.C.4mD.
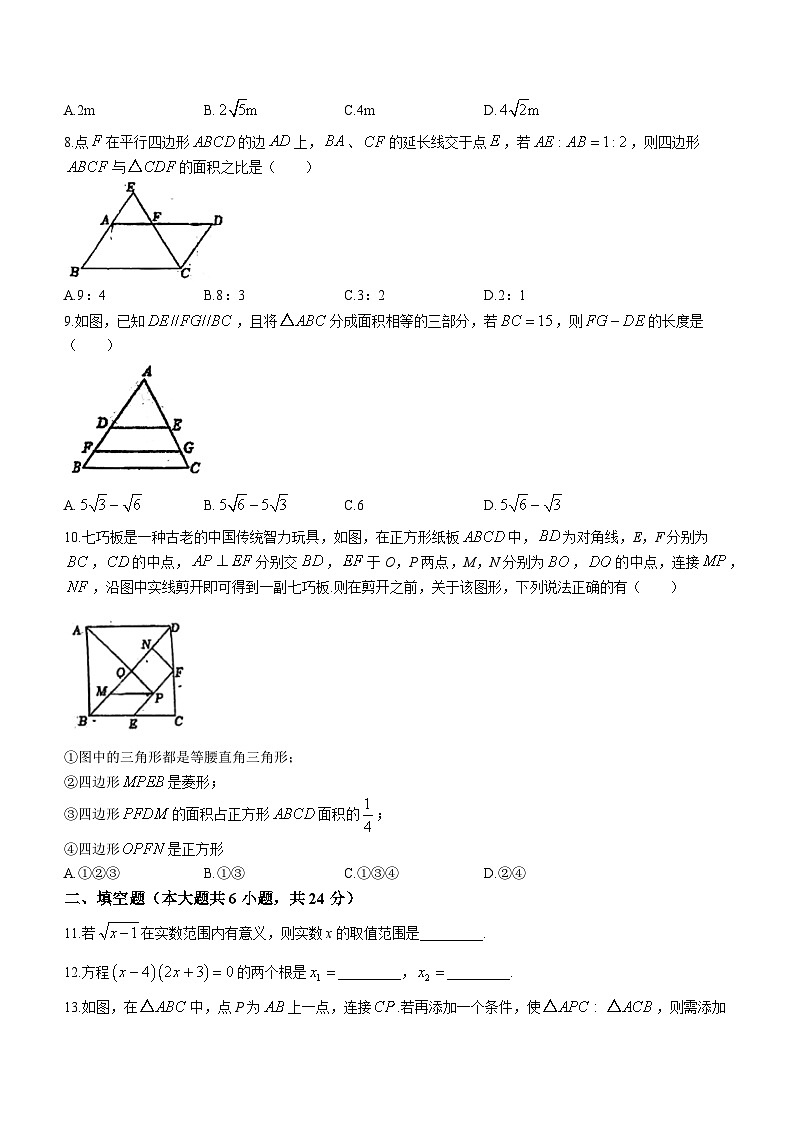
8.点在平行四边形的边上，、的延长线交于点，若，则四边形与的面积之比是（ ）
A.9：4B.8：3C.3：2D.2：1
9.如图，已知，且将分成面积相等的三部分，若，则的长度是（ ）
A.B.C.6D.
10.七巧板是一种古老的中国传统智力玩具，如图，在正方形纸板中，为对角线，E，F分别为，的中点，分别交，于O，P两点，M，N分别为，的中点，连接，，沿图中实线剪开即可得到一副七巧板.则在剪开之前，关于该图形，下列说法正确的有（ ）
①图中的三角形都是等腰直角三角形；
②四边形是菱形；
③四边形的面积占正方形面积的；
④四边形是正方形
A.①②③B.①③C.①③④D.②④
二、填空题（本大题共6小题，共24分）
11.若在实数范围内有意义，则实数x的取值范围是_________.
12.方程的两个根是_________，_________.
13.如图，在中，点P为上一点，连接.若再添加一个条件，使，则需添加的一个条件是_________.
14.如图，矩形的对角线，相交于点，如图，已知，，则为_________.
15.已知a，b是方程的两根，则代数式的值为_________.
16.如图，已知矩形的边长分别为a，b，进行如下操作：第一次，顺次连接矩形各边的中点，得到四边形；第二次，顺次连接四边形各边的中点，得到四边形；…如此反复操作下去，则第次操作后，得到四边形的面积是_________.
三、解答题（本大题共9个小题，共86分）
17.（8分）计算：.
18.（8分）选择适当的方法解下列方程：
（1）；（2）.
19.（8分）如图，在平面直角坐标系中，的顶点坐标分别为，，.
（1）以原点为位似中心，在第一象限内画出的位似图形，使与的相似比为2：1.
（2）将向上平移三个单位长度，得到，直接写出这三个顶点的坐标.
20.（8分）如图，，，点B是线段上的一点，且.已知，，.
（1）证明：.
（2）求线段的长.
21.（8分）已知关于的一元二次方程有两个实数根
（1）求的取值范围；
（2）若，是方程的两个根，且满足，求实数的值.
22.（10分）求证：三角形的重心与一边中点的连线的长是对应中线长的
要求：（1）如图，在中，用尺规作出边上的中线，边上的中线，且与交于点G（不写做法，保留作图痕迹）
（2）在（1）的基础上，写出已知，求证和证明过程.
23.（10分）某超市销售某种商品平均每天可售出20件，每件盈利40元，为了扩大销售，增加盈利，该店采取了降价措施，在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件.
（1）当每件商品降价多少元时，该商店每天销售利润为1200元？
（2）店主想要获得每天1400元的利润，小红认为不可能，请说明理由.
24.（13分）
（1）【感知】如图①，在中，点为的中点，连接并延长交的延长线于点.求证：点是的中点，点是的中点；
（2）【应用】如图②，在四边形中，，，，，点E是的中点，，、的延长线相交于点，求的长；
（3）【扩展】如图③，在中，点是的中点，点是上一点，，、相交于点，求的值.
如图① 如图② 如图③
25.（13分）关于的方程：①和关于的一元二次方程：②（k、m、n均为实数），方程①的解为非正数.
（1）求k的取值范围：
（2）如果方程②的解为负整数，，且k为整数，求整数m的值；
（3）当方程②有两个实数根、，满足，且k为正整数，试判断是否成立？请说明理由.
2023—2024学年第一学期期中联考（初三年数学科）
参考答案及评分标准
一、选择题
二、填空题
三、解答题
17.解：原式
.
18.解：（1），
或，
解得：，.
（2）
或
，.
19.解：（1）如图，即为所求.
（2），，.
20.（1）证明：，，，
，，
，；
（2）解：，，，.
21.解：（1） 关于的一元二次方程有两个实数根，
，解得：.实数的取值范围为.
（2）由根与系数的关系，得：，，
，，
解得：或，又，.
22.（1）如图所示.
（2）已知：在中，、分别是、边上的中线，且与交于点G.
求证：，.
证明：连接，、分别是边、的中点，
，，.
，
，.
22.解：（1）设每件商品降价x元，则每件商品的销售利润为元，平均每天的销售量为件，
根据题意得：，整理得：
解得：，，
当时，，符合题意；
当时，，不符合题意，舍去.
答：当每件商品降价10元时，该商店每天销售利润为1200元；
（2）该店每天不可能获得1400元的利润，理由如下：
假设该店每天可以获得1400元的利润，设每件商品降价y元，则每件商品的销售利润为元，平均每天的销售量为件，
根据题意得：，整理得：
，
所以原方程没有实数根，所以假设不成立，即该店每天不可能获得1400元的利润.
24.（1）证明：中，，，，
在和中，
，，，
点是的中点，点是的中点；
（2）解：与（1）同理可得，，
又由已知可得，四边形是平行四边形，
，四边形是菱形，，
，，，，
；
（3）解：如图，过作交延长线于，
与（1）同理可得，，
，，，
，，，
，，.
25.解：（1）关于的方程的解为，
该方程的解为非正数，，解得，
又关于的方程是一元二次方程，，
综上所述，的取值范围是且；
（2）由（1）可知且，
，，，，
方程②为，
即，
解得：，，
方程②的解为负整数，或，或，
当时，，
当时，，的值为或，
（3）成立，理由如下：由（1）可知且，
又为正整数，，方程②为，
方程②有两个实数根、，，，，
，，
，，
，
当时，，
，，，；
当时，，
，，，；
综上所述，成立.
题号
1
2
3
4
5
6
7
8
9
10
答案
A
C
D
C
A
B
A
D
B
C
题号
11
12
13
14
15
16
答案
4，
（答案不唯一）
6
6