




初中数学青岛版九年级上册2.2 30°,45°,60°角的三角比备课课件ppt
展开1. 能推导并熟记30°、45°、60°角的三角函数值, 并能根据这些值说出对应锐角度数;2. 能熟练计算含有30°、45°、60°角的三角函数的 运算式.
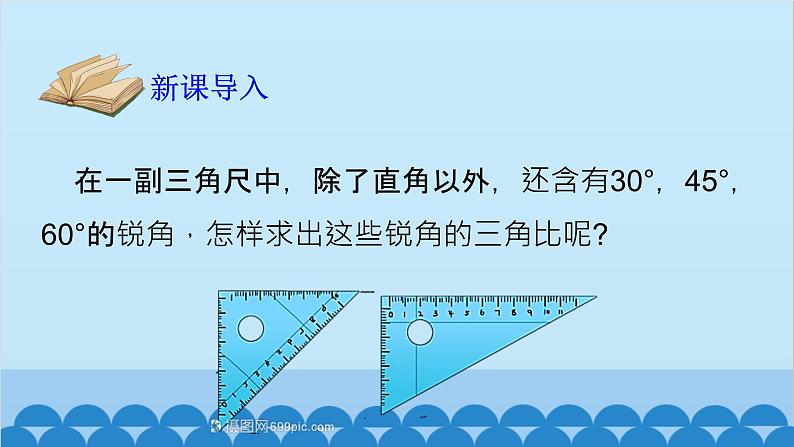
在一副三角尺中,除了直角以外,还含有30°,45°,60°的锐角,怎样求出这些锐角的三角比呢?
(1)要想求出 45°角的正弦、余弦和正切的值,可以考察含 45°锐角的直角三角形.
含 45°角的直角三角形是等腰直角三角形,利用已有的知识,如果已知它的一条直角边,另外两边都可求出,进而可求出45°角的三角比.
作Rt△ABC,使∠C=90°,∠A=45°(图2-5).设a=1,那么b=1.
(2) 怎样才能求出30°角的各三角比的值呢?
含30°角的直角三角形中,目前还不能直接找到三条边之间的关系,能把问题转化为等边三角形吗?
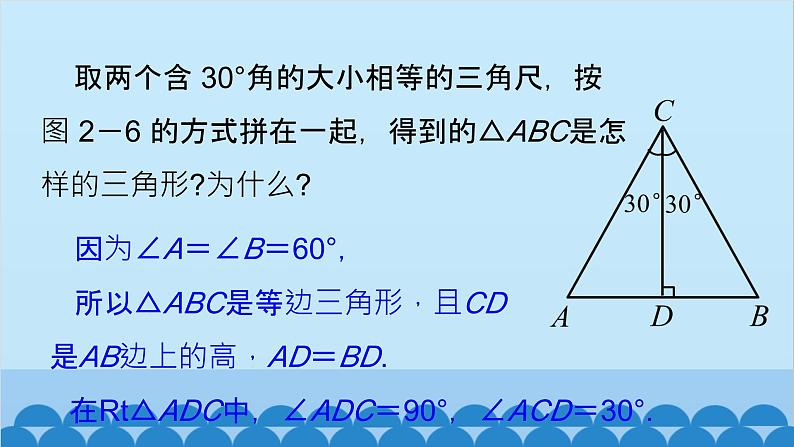
取两个含 30°角的大小相等的三角尺,按图 2-6 的方式拼在一起,得到的△ABC是怎样的三角形?为什么?
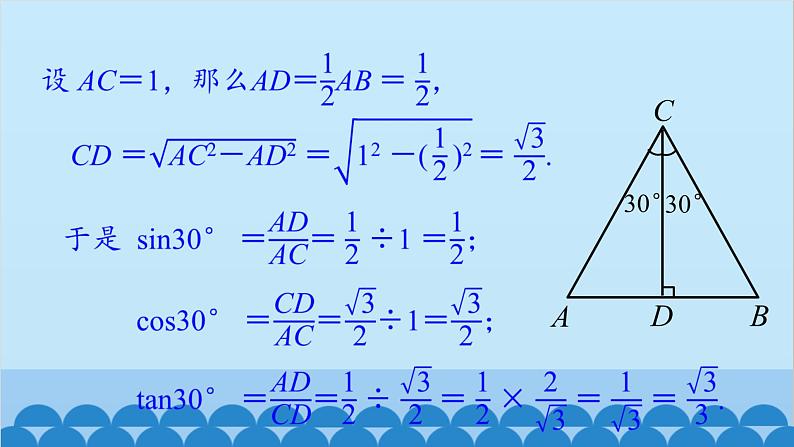
因为∠A=∠B=60°, 所以△ABC是等边三角形,且CD是AB边上的高,AD=BD.
在Rt△ADC中,∠ADC=90°,∠ACD=30°.
(3) 利用图2-6,你会求出60°角的正弦、余弦和正切的值吗?与同学交流.
把30°,45°,60°角的正弦、余弦、正切的值填入下表:
从填写的表格中,你发现了哪些规律?与同学交流.
sinA=cs(90°-∠A);一个锐角的正弦值等于这个角余角的余弦值.csA=sin(90°-∠A);一个锐角的余弦值等于这个角余角的正弦值.tanA·tan(90°-∠A) =1.一个锐角的正切值与这个角余角的正切值互为倒数.
当A,B都是锐角时,如果 sinA = sinB 或 csA = csB 或 tanA = tanB,那么A = B.利用这个结论,知道一个锐角的三角比,可以反过来求这个锐角.
sin 30°· cs 45°;(2) tan 45°- cs 60°.
如图,作等腰直角三角形ABC,∠C= 90°延长边CA到D,使AD = AB,连接DB你能利用图求出22.5°角的正切的值吗?试一试.
1. 求下列各式的值: (1) sin30° + cs 60°; (2) tan 30°· tan 60°;
(3) 2sin 60° - tan 30°;(4) sin 45°·cs 45°+tan 45°.
2. 已知α是锐角. 当α =______时,tan α =1,这时 cs α =________.
1. 求下列各式的值: (1) sin 60°-3tan30°+2cs 45° ;
(4) sin 60°·cs 60°+sin 45°·cs 45°-sin30·cs30°
2. 求下列各式中锐角A的值:
4. 在Rt△ABC中,∠C = 90°,a = 5,b = 15, 求∠A,∠B的度数.
5. 利用类似于本节“挑战自我”中的方法,构造一个图 形,然后利用这个图形求15°及75°角的正切的值.
解:如图所示,在Rt△ABC中∠ABC=30°,∠C=90°,延长CB到点D,使 BD=AB,连接AD.
青岛版九年级上册第2章 解直角三角形2.2 30°,45°,60°角的三角比评课ppt课件: 这是一份青岛版九年级上册第2章 解直角三角形2.2 30°,45°,60°角的三角比评课ppt课件,共16页。PPT课件主要包含了学习目标,问题引入,实验探究,归纳总结,三角比,典例训练,挑战自我,课堂小结等内容,欢迎下载使用。
初中数学青岛版九年级上册2.2 30°,45°,60°角的三角比精品教学ppt课件: 这是一份初中数学青岛版九年级上册2.2 30°,45°,60°角的三角比精品教学ppt课件,文件包含《30°45°60°角的三角比》教学课件ppt、《30°45°60°角的三角比》教学设计doc等2份课件配套教学资源,其中PPT共18页, 欢迎下载使用。
初中青岛版2.2 30°,45°,60°角的三角比教案配套课件ppt: 这是一份初中青岛版2.2 30°,45°,60°角的三角比教案配套课件ppt,共10页。PPT课件主要包含了∠A的正弦,∠A的余弦,∠A的正切,导入新课,说出下列各式值,余弦随着角度的增加而等内容,欢迎下载使用。













