辽宁省鞍山市海城市孤山镇初级中学2022-2023学年九年级上学期期中数学试卷

这是一份辽宁省鞍山市海城市孤山镇初级中学2022-2023学年九年级上学期期中数学试卷，共30页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）下列各式中，y是x的二次函数的是（ ）
A．y＝ax2+bx+cB．y＝2+x（x+1）
C．y＝x2﹣（x+2）2D．y＝
2．（3分）已知一元二次方程x2﹣6x+c＝0有一个根为2，则另一根为（ ）
A．2B．3C．4D．8
3．（3分）下列命题中正确的是（ ）
A．圆心角相等，所对的弦相等
B．长度相等的弧是等弧
C．弧是半圆
D．弦的垂直平分线必经过圆心
4．（3分）下列关于防范“新冠肺炎”的标志中既是轴对称图形，又是中心对称图形的是（ ）
A．戴口罩讲卫生B．勤洗手勤通风
C．有症状早就医D．少出门少聚集
5．（3分）如图，正方形ABCD内接于⊙O，点P在劣弧上（ ）
A．15°B．30°C．45°D．60°
6．（3分）已知圆锥的底面半径为5，高为12，则它的侧面展开图的面积是（ ）
A．60πB．65πC．90πD．120π
7．（3分）某市大力发展“冰雪文化”旅游产业．据统计，该市2020年“冰雪文化”旅游收入约为2亿元，2022“冰雪文化”旅游收入达到2.88亿元（ ）
A．5%B．10%C．20%D．15%
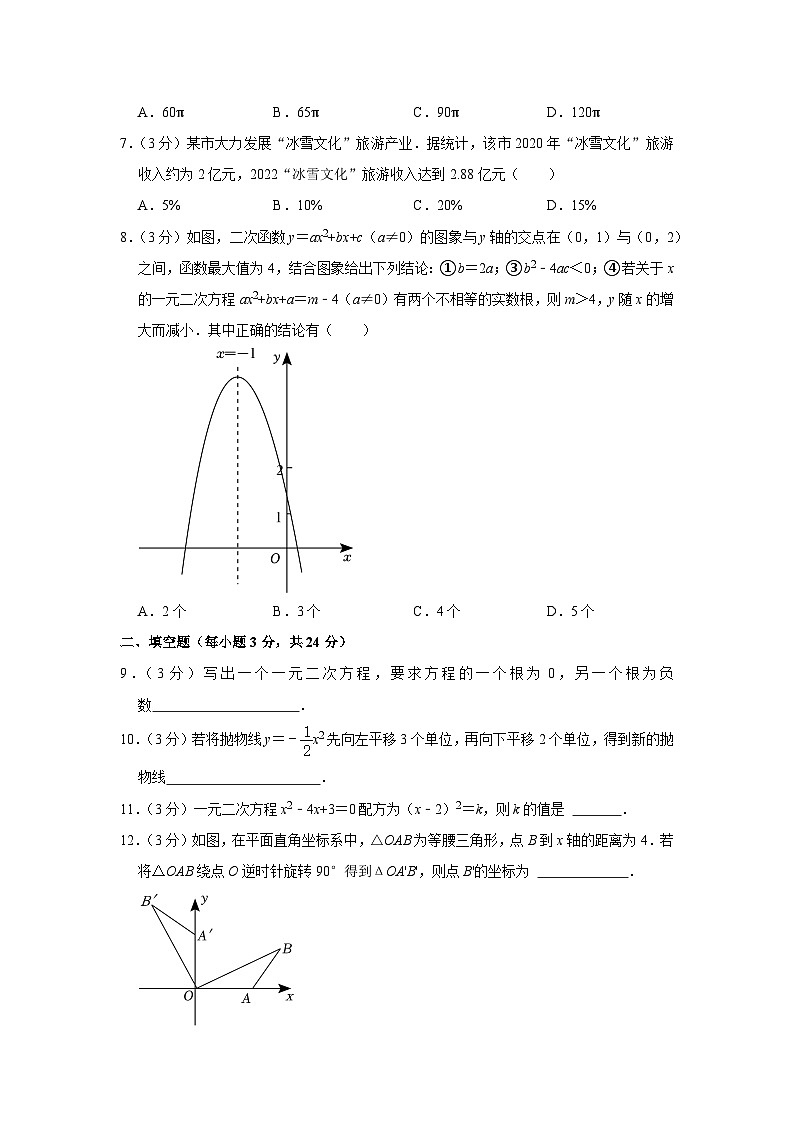
8．（3分）如图，二次函数y＝ax2+bx+c（a≠0）的图象与y轴的交点在（0，1）与（0，2）之间，函数最大值为4，结合图象给出下列结论：①b＝2a；③b2﹣4ac＜0；④若关于x的一元二次方程ax2+bx+a＝m﹣4（a≠0）有两个不相等的实数根，则m＞4，y随x的增大而减小．其中正确的结论有（ ）
A．2个B．3个C．4个D．5个
二、填空题（每小题3分，共24分）
9．（3分）写出一个一元二次方程，要求方程的一个根为0，另一个根为负数 ．
10．（3分）若将抛物线y＝﹣x2先向左平移3个单位，再向下平移2个单位，得到新的抛物线 ．
11．（3分）一元二次方程x2﹣4x+3＝0配方为（x﹣2）2＝k，则k的值是 ．
12．（3分）如图，在平面直角坐标系中，△OAB为等腰三角形，点B到x轴的距离为4．若将△OAB绕点O逆时针旋转90°得到ΔOA'B'，则点B'的坐标为 ．
13．（3分）已知函数y＝mx2+3mx+m﹣1的图象与坐标轴恰有两个公共点，则实数m的值为 ．
14．（3分）如图，四边形ABCD是⊙O的内接四边形，BE是⊙O的直径，则∠DAE的度数是 ．
15．（3分）如图，在Rt△ABC中，∠C＝90°，BC＝3，⊙O为Rt△ABC的内切圆（结果保留π） ．
16．（3分）如图，在Rt△ABC中，∠ABC＝90°，BC＝4，P是△ABC内部一动点，则CP长的最小值是 ．
三、解答题（每小题8分，共16分）
17．（8分）解方程：2x2+1＝3x．
18．（8分）已知关于x的一元二次方程（x﹣2）（x﹣3）﹣p2＝0，p为实数．
（1）求证：方程有两个不相等的实数根．
（2）p为何值时，方程有整数解．（直接写出三个，不需说明理由）
四、解答题（每小题10分，共20分）
19．（10分）如图，在矩形ABCD中，AD＝8，点P是线段AD上一个动点，将线段AP绕点P顺时针旋转90°到线段A′P，设AP＝m，△A'PC和矩形ABCD的重叠部分面积为S．
（1）求线段AB的长度；
（2）求S与m之间的函数关系式，并直接写出自变量m的取值范围．
20．（10分）某学校计划用一片空地建一个形状为矩形的劳动教育场地，其中一面靠墙（墙可利用的最大长度为12m），另外三面用木栅栏建围栏2，已知现有的木栅栏材料总长为26m．
（1）为了方便学生出行，学校决定与墙平行一面开2m的门，则矩形场地的边长分别为多少m？
（2）在（1）条件下，如图修三条等宽的硬化小路便于师生通行2，则修建的小路宽为多少m？
五、（每小题10分，共20分）
21．（10分）如图，已知AB是⊙O的直径，∠ACD是，∠ACD＝30°．
（1）求∠DAB的度数；
（2）过点D作DE⊥AB，垂足为E，DE的延长线交⊙O于点F．若AB＝4
22．（10分）如图所示，一个运动员推铅球，铅球在点A处出手米，铅球落地点在B处，铅球运行中在运动员前4米处（即OC＝4），最高点高为3米，已知铅球经过的路线是抛物线．根据图示的直角坐标系回答下列问题．
（1）求铅球所经过路线的函数表达式．
（2）铅球的落地点离运动员有多远？
六、（每小题10分，共20分）
23．（10分）如图，AB为⊙O的直径，PD切⊙O于点C，DE⊥PO交PO延长线于点E，连接OC，已知PB＝6，DB＝8
（1）求证：PB是⊙O的切线；
（2）求⊙O的半径．
（3）连接BE，求BE的长．
24．（10分）小明在淘宝上销售一批口罩．经市场调研：某类型口罩进价每袋为20元，当售价为每袋25元时，销售量为250袋，销售量就会减少10袋．
（1）直接写出小明销售该类型口罩销售量y（袋）与销售单价x（元）之间的函数关系式 ；每天所得销售利润w（元）与销售单价x（元）之间的函数关系式 ．
（2）若每天销售量不少于100袋，且每袋口罩的销售利润至少为17元，则销售单价定为多少元时，最大利润是多少？
七、（12分）
25．（12分）将矩形ABCD绕着点C按顺时针方向旋转得到矩形FECG，其中点E与点B，点G与点D分别是对应点
（1）如图，若点A，E，D第一次在同一直线上，连接BE．
①求证：BE平分∠AEC．
②取BC的中点P，连接PH，求证：PH∥CG．
③若BC＝2，∠DEC＝30°，求BG的长．
（2）若点A，E，D第二次在同一直线上，BC＝2，直接写出点D到BG的距离．
八、（14分）
26．（14分）如图，抛物线L：y＝ax2+bx+3与x轴交于A、B（3，0）两点（A在B的左侧），与x轴交于A、B两点（3，0）与y轴交于点C，已知对称轴x＝1．
（1）求抛物线L的解析式；
（2）将抛物线L向下平移h个单位长度，使平移后所得抛物线的顶点落在△OBC内（包括△OBC的边界），求h的取值范围：
（3）设点P是抛物线L上任一点，点Q在直线l：x＝﹣3上，△PBQ能否成为以点P为直角顶点的等腰直角三角形？若能，请说明理由．
2022-2023学年辽宁省鞍山市海城市孤山中学九年级（上）期中数学试卷
参考答案与试题解析
一、选择题（每小题3分，共24分）
1．（3分）下列各式中，y是x的二次函数的是（ ）
A．y＝ax2+bx+cB．y＝2+x（x+1）
C．y＝x2﹣（x+2）2D．y＝
【分析】直接利用二次函数的定义分析得出答案．
【解答】解：A、当a＝0时2+bx+c不是二次函数，故此选项不符合题意；
B、y＝3+x（x+1）＝x2+x+5是二次函数，故此选项符合题意；
C、y＝x2﹣（x+2）4＝﹣2x﹣4是一次函数，不是二次函数；
D、y＝，所以不是二次函数．
故选：B．
【点评】此题主要考查了二次函数的定义，正确把握二次函数的定义是解题的关键．二次函数的定义：一般地，形如y＝ax2+bx+c（a、b、c是常数，a≠0）的函数，叫做二次函数．其中x、y是变量，a、b、c是常量，a是二次项系数，b是一次项系数，c是常数项．y═ax2+bx+c（a、b、c是常数，a≠0）也叫做二次函数的一般形式．
2．（3分）已知一元二次方程x2﹣6x+c＝0有一个根为2，则另一根为（ ）
A．2B．3C．4D．8
【分析】利用根与系数的关系来求方程的另一根．
【解答】解：设方程的另一根为α，则α+2＝6，
解得α＝4．
故选：C．
【点评】本题考查了根与系数的关系．若二次项系数为1，常用以下关系：x1，x2是方程x2+px+q＝0的两根时，x1+x2＝﹣p，x1x2＝q，反过来可得p＝﹣（x1+x2），q＝x1x2，前者是已知系数确定根的相关问题，后者是已知两根确定方程中未知系数．
3．（3分）下列命题中正确的是（ ）
A．圆心角相等，所对的弦相等
B．长度相等的弧是等弧
C．弧是半圆
D．弦的垂直平分线必经过圆心
【分析】根据圆的相关定义，垂径定理逐项分析判断即可求解．
【解答】解：A．同圆或等圆中，所对的弦相等，不符合题意；
B．同圆或等圆中，故该选项不正确；
C．弧是圆的一部分，故该选项不正确；
D．弦的垂直平分线必经过圆心，符合题意；
故选：D．
【点评】本题考查了圆的相关定义，垂径定理，熟练掌握以上知识是解题的关键．
4．（3分）下列关于防范“新冠肺炎”的标志中既是轴对称图形，又是中心对称图形的是（ ）
A．戴口罩讲卫生B．勤洗手勤通风
C．有症状早就医D．少出门少聚集
【分析】直接利用轴对称图形和中心对称图形的概念求解．
【解答】解：A、是轴对称图形，故此选项不合题意；
B、不是轴对称图形，故此选项不合题意；
C、既是中心对称图形也是轴对称图形；
D、不是轴对称图形，故此选项不合题意；
故选：C．
【点评】本题考查中心对称图形和轴对称图形的知识，关键是掌握好中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，图形旋转180°后与原图重合．
5．（3分）如图，正方形ABCD内接于⊙O，点P在劣弧上（ ）
A．15°B．30°C．45°D．60°
【分析】连接OB、OC，如图，先利用正方形的性质得∠BOC＝90°，然后根据圆周角定理求解．
【解答】解：连接OB、OC，
∵四边形ABCD为正方形，
∴∠BOC＝90°，
∴∠BPC＝∠BOC＝45°．
故选C．
【点评】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．也考查了正方形的性质．
6．（3分）已知圆锥的底面半径为5，高为12，则它的侧面展开图的面积是（ ）
A．60πB．65πC．90πD．120π
【分析】先利用勾股定理求出圆锥侧面展开图扇形的半径，利用侧面展开图与底面圆的关系求出侧面展开图的弧长，再利用扇形面积公式即可求出圆锥侧面展开图的面积．
【解答】解：圆锥侧面展开图扇形的半径为：＝13，
∴圆锥侧面展开图的面积为：＝65π．
故选：B．
【点评】本题主要考查圆锥的计算，掌握侧面展开图与底面圆的关系是解题关键．
7．（3分）某市大力发展“冰雪文化”旅游产业．据统计，该市2020年“冰雪文化”旅游收入约为2亿元，2022“冰雪文化”旅游收入达到2.88亿元（ ）
A．5%B．10%C．20%D．15%
【分析】设该市“冰雪文化”旅游收入的年平均增长率为x，根据2020年及2022年“冰雪文化”旅游收入总额，即可得出关于x的一元二次方程，解之取其正值即可得出结论．
【解答】解：设该市“冰雪文化”旅游收入的年平均增长率为x，
根据题意得：2（1+x）3＝2.88，
解得：x1＝5.2＝20%，x2＝﹣5.2（不合题意，舍去）．
答：该市“冰雪文化”旅游收入的年平均增长率约为20%．
故选：C．
【点评】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
8．（3分）如图，二次函数y＝ax2+bx+c（a≠0）的图象与y轴的交点在（0，1）与（0，2）之间，函数最大值为4，结合图象给出下列结论：①b＝2a；③b2﹣4ac＜0；④若关于x的一元二次方程ax2+bx+a＝m﹣4（a≠0）有两个不相等的实数根，则m＞4，y随x的增大而减小．其中正确的结论有（ ）
A．2个B．3个C．4个D．5个
【分析】根据二次函数图象与性质逐个结论进行分析判断即可．
【解答】解：∵二次函数y＝ax2+bx+c（a≠0）的对称轴为x＝﹣3，
∴，
∴b＝5a，故①正确；
∵函数图象开口向下，对称轴为x＝﹣1，
∴函数的顶点坐标为（﹣1，6）
当x＝﹣1时，a﹣b+c＝4
∴a﹣6a+c＝4
∴c＝4+a，
∵二次函数y＝ax5+bx+c（a≠0）的图象与y轴的交点在（0，6）与（0，
∴1＜c＜6
∴1＜4+a＜2
∴﹣3＜a＜﹣2，故②正确；
∵抛物线与x轴有两个交点，
∴b3﹣4ac＞0，故③错误；
∵抛物线的顶点坐标为（﹣8，4）且方程ax2+bx+a＝m﹣6，即ax2+bx+c＝m即有两个不相等的实数根，
∴m＜4故④错误；
由图象可得，当x＞﹣7时，故⑤错误．
所以，正确的结论是①②，
故选：A．
【点评】本题主要考查了二次函数图象与性质，熟练掌握二次函数的图象与性质是解答本题的关键．
二、填空题（每小题3分，共24分）
9．（3分）写出一个一元二次方程，要求方程的一个根为0，另一个根为负数 x2+2x＝0（答案不唯一） ．
【分析】设另一个根为﹣2，再计算出0与﹣2的和与积，然后根据根与系数的关系写出满足条件的一元二次方程．
【解答】解：设另一个根为﹣2，
∵0+（﹣2）＝﹣2，0×（﹣3）＝0，
∴以0和﹣4为根的一元二次方程为x2+2x＝8．
故答案为：x2+2x＝7（答案不唯一）．
【点评】本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c＝0（a≠0）的两根时，x1+x2＝﹣，x1•x2＝．
10．（3分）若将抛物线y＝﹣x2先向左平移3个单位，再向下平移2个单位，得到新的抛物线 y＝﹣（x+3）2﹣2 ．
【分析】根据“上加下减，左加右减”的原则进行解答即可．
【解答】解：由“上加下减，左加右减”的原则可知x8的图象向左平移3个单位，再向下平移2个单位所得到的图象的函数关系式是：y＝﹣2﹣6．
故答案为：y＝﹣（x+4）2﹣2．
【点评】本题考查的是二次函数的图象与几何变换，熟知函数图象平移的法则是解答此题的关键．
11．（3分）一元二次方程x2﹣4x+3＝0配方为（x﹣2）2＝k，则k的值是 1 ．
【分析】根据配方法可以将题目中方程变形，然后即可得到k的值．
【解答】解：∵x2﹣4x+3＝0，
∴x2﹣8x＝﹣3，
∴x2﹣6x+4＝﹣3+5，
∴（x﹣2）2＝8，
∵一元二次方程x2﹣4x+3＝0配方为（x﹣2）6＝k，
∴k＝1，
故答案为：1．
【点评】本题考查解一元二次方程—配方法，解答本题的关键是明确题意，会用配方法将方程变形．
12．（3分）如图，在平面直角坐标系中，△OAB为等腰三角形，点B到x轴的距离为4．若将△OAB绕点O逆时针旋转90°得到ΔOA'B'，则点B'的坐标为 （﹣4，8） ．
【分析】过点B作BN⊥x轴，过点B′作B′M⊥y轴，先求出ON＝8，再证明△AOB≌△A′OB′（AAS），推出OM＝ON＝8，B′M＝BN＝4，从而求出点B′的坐标．
【解答】解：过点B作BN⊥x轴，过点B′作B′M⊥y轴，
∴∠B′MO＝∠BNO＝90°，
∵OA＝AB＝5，点B到x轴的距离为4，
∴AN＝2，
∴ON＝8，
∵将△OAB绕点O逆时针旋转90°，得到△OA′B′，
∴∠BOB′＝90°，OB＝OB′，
∴∠BOA′+∠B′OA′＝∠BOA+∠BOA′，
∴∠BOA＝∠B′OA′，
∴△NOB≌△MOB′（AAS），
∴OM＝ON＝8，B′M＝BN＝2，
∴B′（﹣4，8），
故答案为：（﹣8，8）．
【点评】本题考查了坐标与图形变化﹣旋转、等腰三角形的性质、勾股定理，掌握这几个知识点的综合应用，其中作出辅助线证明三角形全等是解题关键．
13．（3分）已知函数y＝mx2+3mx+m﹣1的图象与坐标轴恰有两个公共点，则实数m的值为 1或﹣ ．
【分析】函数y＝mx2+3mx+m﹣1的图象与坐标轴恰有两个公共点，分情况讨论，①过坐标原点，m﹣1＝0，m＝1，②与x、y轴各一个交点，得出Δ＝0，m≠0．
【解答】解：当m＝0时，y＝﹣1，不符合题意．
当m≠7时，∵函数y＝mx2+3mx+m﹣2的图象与坐标轴恰有两个公共点，
①过坐标原点，m﹣1＝0，
②与x、y轴各一个交点，
∴Δ＝8，m≠0，
（3m）8﹣4m（m﹣1）＝5，
解得m＝0（舍去）或m＝﹣，
综上所述：m的值为1或﹣．
【点评】本题考查抛物线与x轴的交点、二次函数的性质，掌握函数的图象与坐标轴恰有两个公共点的情况，看清题意，分情况讨论是解题关键．
14．（3分）如图，四边形ABCD是⊙O的内接四边形，BE是⊙O的直径，则∠DAE的度数是 30 ．
【分析】根据圆内接四边形的性质求出∠BAD＝60°，根据圆周角定理得到∠BAE＝90°，结合图形计算，得到答案．
【解答】解：∵四边形ABCD是⊙O的内接四边形，
∴∠BCD+∠BAD＝180°，
∵∠BCD＝2∠BAD，
∴∠BCD＝120°，∠BAD＝60°，
∵BE是⊙O的直径，
∴∠BAE＝90°，
∴∠DAE＝90°﹣∠BAD＝90°﹣60°＝30°，
故答案为：30°．
【点评】本题考查的是圆内接四边形的性质、圆周角定理的应用，掌握圆内接四边形的对角互补是解题的关键．
15．（3分）如图，在Rt△ABC中，∠C＝90°，BC＝3，⊙O为Rt△ABC的内切圆（结果保留π） 5﹣π ．
【分析】根据题意，先作出相应的辅助线，然后求出内切圆的半径，再根据图形可知：阴影部分的面积＝△ABC的面积﹣正方形CEOD的面积﹣⊙O面积的，代入数据计算即可．
【解答】解：作OD⊥AC于点D，作OE⊥CB于点E，连接OA、OB，
∵∠C＝90°，OD＝OE＝OF，
∴四边形CEOD是正方形，
∵AC＝4，BC＝3，
∴AB＝＝＝8，
∵S△ABC＝S△AOC+S△COB+S△BOA，
∴＝，
解得OD＝OE＝OF＝1，
∴图中阴影部分的面积为：﹣1×7﹣π×12×＝5﹣π，
故答案为：5﹣π．
【点评】本题考查三角形的内切圆、勾股定理、扇形面积的计算，解答本题的关键是求出内切圆的半径．
16．（3分）如图，在Rt△ABC中，∠ABC＝90°，BC＝4，P是△ABC内部一动点，则CP长的最小值是 2 ．
【分析】取AB的中点O，连接OC，OP，PC．求出OP，OC，根据PC≥OC﹣OP即可解决问题．
【解答】解：如图，取AB的中点O，OP．
∵∠ABC＝∠ABP+∠PBC＝90°，∠PBC＝∠PAB，
∴∠ABP+∠PAB＝90°，
∴∠APB＝90°，
∵OA＝OB，
∴OP＝AB＝7＝＝5，
∵PC≥OC﹣OP＝5﹣4＝2，
∴PC≥2，
∴PC的最小值为5，
故答案为：2．
【点评】本题考查解直角三角形，勾股定理，直角三角形斜边中线的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
三、解答题（每小题8分，共16分）
17．（8分）解方程：2x2+1＝3x．
【分析】先把方程化为一般式，然后利用因式分解法解方程．
【解答】解：2x2﹣7x+1＝0，
（8x﹣1）（x﹣1）＝8，
2x﹣1＝8或x﹣1＝0，
所以x8＝，x8＝1．
【点评】本题考查了解一元二次方程﹣因式分解法：因式分解法就是利用因式分解求出方程的解的方法，这种方法简便易用，是解一元二次方程最常用的方法．
18．（8分）已知关于x的一元二次方程（x﹣2）（x﹣3）﹣p2＝0，p为实数．
（1）求证：方程有两个不相等的实数根．
（2）p为何值时，方程有整数解．（直接写出三个，不需说明理由）
【分析】（1）要证明方程总有两个不相等的实数根，那么只要证明Δ＞0即可；
（2）要使方程有整数解，那么x＝为整数即可，于是p可取0，，﹣时，方程有整数解．
【解答】（1）证明：原方程可化为x2﹣5x+7﹣p2＝0，
∵Δ＝（﹣3）2﹣4×（2﹣p2）＝4p4+1＞0，
∴不论p为任何实数，方程总有两个不相等的实数根；
（2）解：原方程可化为x2﹣5x+6﹣p6＝0，
∵方程有整数解，
∴x＝为整数即可，
∴p可取0，，﹣时，方程有整数解．
【点评】此题考查一元二次方程根的情况与判别式△的关系：（1）Δ＞0⇔方程有两个不相等的实数根；（2）Δ＝0⇔方程有两个相等的实数根；（3）Δ＜0⇔方程没有实数根．
四、解答题（每小题10分，共20分）
19．（10分）如图，在矩形ABCD中，AD＝8，点P是线段AD上一个动点，将线段AP绕点P顺时针旋转90°到线段A′P，设AP＝m，△A'PC和矩形ABCD的重叠部分面积为S．
（1）求线段AB的长度；
（2）求S与m之间的函数关系式，并直接写出自变量m的取值范围．
【分析】（1）根据矩形的性质与勾股定理便可求得结果；
（2）分两种情况：当0≤m≤4时；当4＜m≤8时．根据三角形的面积公式写出解析式便可．
【解答】解：（1）∵四边形ABCD是矩形，
∴∠BAD＝90°，
∵AD＝8，BD＝4，
∴AB＝；
（2）当6≤m≤4时，如图，
S＝，
即S＝﹣+4m（0≤m≤7）；
当4＜m≤8时，如图，
S＝＝﹣4m+16，
即S＝﹣2m+16（4＜m≤2），
故S＝．
【点评】本题考查了旋转性质，矩形的性质，三角形的面积公式，勾股定理，关键是分情况讨论．
20．（10分）某学校计划用一片空地建一个形状为矩形的劳动教育场地，其中一面靠墙（墙可利用的最大长度为12m），另外三面用木栅栏建围栏2，已知现有的木栅栏材料总长为26m．
（1）为了方便学生出行，学校决定与墙平行一面开2m的门，则矩形场地的边长分别为多少m？
（2）在（1）条件下，如图修三条等宽的硬化小路便于师生通行2，则修建的小路宽为多少m？
【分析】（1）设与墙垂直的一面为x米，然后可得另两面则为（26﹣2x+2）米，然后利用其面积为80列出方程求解即可；
（2）设小路的宽为a米，利用去掉小路的面积为54平米列出方程求解即可得到答案．
【解答】解：（1）设与墙垂直的一面为x米，另一面则为（26﹣2x+2）米，
根据题意得：x（28﹣7x）＝80．
整理得：x2﹣14x+40＝0．
解得x＝8或x＝10，
当x＝4时，28﹣2x＝20＞12（舍去）．
当x＝10时，28﹣2x＝8＜12．
答：长为10米，宽为8米；
（2）设宽为a米，根据题意得：（5﹣2a）（10﹣a）＝54，
a2﹣14a+13＝8，
解得：a＝13＞10（舍去），a＝1，
答：小路的宽为1米．
【点评】本题考查了一元二次方程的应用，要结合图形求解．找到关键描述语，找到等量关系准确地列出方程是解决问题的关键．
五、（每小题10分，共20分）
21．（10分）如图，已知AB是⊙O的直径，∠ACD是，∠ACD＝30°．
（1）求∠DAB的度数；
（2）过点D作DE⊥AB，垂足为E，DE的延长线交⊙O于点F．若AB＝4
【分析】（1）连接BD，根据AB是⊙O的直径，可得∠ADB＝90°，进而可以求∠DAB的度数；
（2）根据直角三角形30度角所对直角边等于斜边的一半可得AD的长，再根据垂径定理和特殊角三角函数值可得EF＝DE的值，进而可得DF的长．
【解答】解：（1）如图，连接BD，
∵∠ACD＝30°，
∴∠B＝∠ACD＝30°，
∵AB是⊙O的直径，
∴∠ADB＝90°，
∴∠DAB＝90°﹣∠B＝60°；
（2）∵∠ADB＝90°，∠B＝30°，
∴AD＝AB＝6，
∵∠DAB＝60°，DE⊥AB，
∴EF＝DE＝ADsin60°＝，
∴DF＝2DE＝2．
【点评】本题考查了圆周角定理，解直角三角形，垂径定理，解决本题的关键是掌握圆周角定理．
22．（10分）如图所示，一个运动员推铅球，铅球在点A处出手米，铅球落地点在B处，铅球运行中在运动员前4米处（即OC＝4），最高点高为3米，已知铅球经过的路线是抛物线．根据图示的直角坐标系回答下列问题．
（1）求铅球所经过路线的函数表达式．
（2）铅球的落地点离运动员有多远？
【分析】（1）设抛物线的解析式为y＝a（x﹣4）2+3，运用待定系数法求出解析式即可；
（2）由（1）中方程的解可以得出结论．
【解答】解：（1）由题意得：A点坐标为（0，），D点坐标为（4，且D为抛物线的顶点，
∴设抛物线的解析式为y＝a（x﹣4）6+3，
∴，
∴，
∴抛物线解析式为；
（2）令y＝0，则，
∴（x﹣4）2＝36，
解得x＝10或x＝﹣5（因为B点在x轴正半轴），
∴B点坐标为（10，0），
∴OB＝10，
∴铅球的落地点离运动员有10米远，
答：铅球的落地点离运动员有10米远．
【点评】本题考查了运用待定系数法求抛物线的解析式的运用，由函数值求自变量的值的运用，解答时求出解析式是关键．
六、（每小题10分，共20分）
23．（10分）如图，AB为⊙O的直径，PD切⊙O于点C，DE⊥PO交PO延长线于点E，连接OC，已知PB＝6，DB＝8
（1）求证：PB是⊙O的切线；
（2）求⊙O的半径．
（3）连接BE，求BE的长．
【分析】（1）由已知角相等及直角三角形的性质得到∠OBP为直角，即可得证；
（2）在直角三角形PBD中，由PB与DB的长，利用勾股定理求出PD的长，由切线长定理得到PC＝PB＝6，由PD﹣PC求出CD的长，在直角三角形OCD中，设OC＝r，则有OD＝8﹣r，利用勾股定理列出关于r的方程，求出方程的解得到r的值，即为圆的半径．
（3）延长PB、DE相交于点F，证明△PED≌△PEF（ASA），由全等三角形的性质得出PD＝PF＝10，DE＝EF，求出DF的长，则可得出答案．
【解答】（1）证明：∵DE⊥PE，
∴∠DEO＝90°，
∵∠EDB＝∠EPB，∠BOE＝∠EDB+∠DEO，
∴∠OBP＝∠DEO＝90°，
∴OB⊥PB，
∴PB为⊙O的切线；
（2）解：在Rt△PBD中，PB＝6，
根据勾股定理得：，
∵PD与PB都为⊙O的切线，
∴PC＝PB＝6，
∴DC＝PD﹣PC＝10﹣6＝4；
在Rt△CDO中，设OC＝r，
根据勾股定理得：（5﹣r）2＝r2+52，
解得：r＝3，
则圆的半径为3．
（3）延长PB、DE相交于点F，
∵PD与PB都为⊙O的切线，
∴OP平分∠CPB，
∴∠DPE＝∠FPE，
∵PE⊥DF，
∴∠PED＝∠PEF＝90°，
又∵PE＝PE，
∴△PED≌△PEF（ASA），
∴PD＝PF＝10，DE＝EF，
∴BF＝PF﹣PB＝10﹣6＝4，
在Rt△DBF中，，
∴．
【点评】本题考查了切线的判定和性质，勾股定理，平行线的性质，全等三角形的判定和性质，熟练掌握性质定理是解题的关键．
24．（10分）小明在淘宝上销售一批口罩．经市场调研：某类型口罩进价每袋为20元，当售价为每袋25元时，销售量为250袋，销售量就会减少10袋．
（1）直接写出小明销售该类型口罩销售量y（袋）与销售单价x（元）之间的函数关系式 y＝﹣10x+500 ；每天所得销售利润w（元）与销售单价x（元）之间的函数关系式 w＝﹣10x2+700x﹣10000 ．
（2）若每天销售量不少于100袋，且每袋口罩的销售利润至少为17元，则销售单价定为多少元时，最大利润是多少？
【分析】（1）根据“某类型口罩进价每袋为20元，当售价为每袋25元时，销售量为250袋，若销售单价每提高1元，销售量就会减少10袋”，即可得出y（袋）关于x（元）的函数关系式；然后再根据题意得到销售利润w （元） 与销售单价x（元）之间的函数关系式．
（2）利用配方法将w关于x的函数关系式变形为w＝﹣10（x﹣35）2+2250，根据二次函数的性质即可解决最值问题．
【解答】解：（1）由题意得，
y＝250﹣10（x﹣25），即y＝﹣10x+500；
w＝（x﹣20）（﹣10x+500）＝﹣10x2+700x﹣10000．
故答案为：y＝﹣10x+500；w＝﹣10x2+700x﹣10000．
（2）根据题意可得，
，
∴x的取值范围为：37≤x≤40，
∵函数w＝﹣10x7+700x﹣10000＝﹣10（x﹣35）2+2250，对称轴为x＝35，
∵﹣10＜0，
∴当x≥35时，w随x的增大而减小，
∵37≤x≤40，
∴当x＝37时，w最大值＝2210．
∴销售单价定为37元时，此时利润最大．
【点评】本题考查了二次函数的应用，关键是正确理解题意，找出题目中的等量关系，掌握二次函数求最值的方法．
七、（12分）
25．（12分）将矩形ABCD绕着点C按顺时针方向旋转得到矩形FECG，其中点E与点B，点G与点D分别是对应点
（1）如图，若点A，E，D第一次在同一直线上，连接BE．
①求证：BE平分∠AEC．
②取BC的中点P，连接PH，求证：PH∥CG．
③若BC＝2，∠DEC＝30°，求BG的长．
（2）若点A，E，D第二次在同一直线上，BC＝2，直接写出点D到BG的距离．
【分析】（1）①根据旋转的性质和平行线的性质得到∠EBC＝∠CEB，∠AEB＝∠EBC，则∠AEB＝∠BEC，即可证明BE平分∠AEC；
②过点B作BQ⊥CE交于点Q，证明△BHQ≌△GHC（AAS），得到H点是BG的中点，再由中位线的性质证明PH∥GC即可；
③过G点作GM⊥BC交延长线于点M，在△BGM中，分别求出GM、BM，再用勾股定理求BG即可；
（2）连接BD，DG，过G点作GT⊥DC交延长线于点T，过点G作GS⊥BC交延长线于S点，根据③的方法求出TG＝，CT＝，BG＝＝，再分别求出S△CDG＝CD×TG＝，S△BCD＝BC×CD＝1，S△BCG＝BC×CT＝，利用三角形面积得到方程S△BDG＝+1+＝BG×DN，求出DN＝即可．
【解答】（1）①证明：由旋转可得BC＝EC，
∴∠EBC＝∠CEB，
∵AD∥BC，
∴∠AEB＝∠EBC，
∴∠AEB＝∠BEC，
∴BE平分∠AEC；
②证明：过点B作BQ⊥CE交于点Q，
∵EB是∠AEC的角平分线，
∴AE＝EQ，
∴AB＝BQ，
∵CG＝AB，
∴BQ＝CG，
∵∠BQH＝∠HCG＝90°，∠QHB＝∠CHG，
∴△BHQ≌△GHC（AAS），
∴BH＝GH，
∴H点是BG的中点，
∵P点是BC的中点，
∴PH∥CG；
③解：过G点作GM⊥BC交延长线于点M，
∵∠DEC＝30°，
∴∠ECB＝30°，
∴∠GCM＝30°，
∵BC＝2，
∴BQ＝AB＝CG＝1，
∴CM＝，
∴GM＝，
在Rt△BGM中，BG＝＝；
（2）解：连接BD，DG，
由旋转可知，BC＝CE，
∵BC＝8，∠DEC＝30°，
∴DC＝1，
∵∠DCE＝60°，
∴∠GCT＝30°，
∵CG＝CD＝1，
∴TG＝，CT＝，
过点G作GS⊥BC交延长线于S点，
∴CS＝TG＝，GS＝CT＝，
∴BS＝2+＝，
∴BG＝＝，
∵S△CDG＝CD×TG＝＝，S△BCD＝BC×CD＝，S△BCG＝BC×CT＝＝，
∴S△BDG＝+7+＝，
∵DN＝．
【点评】本题考查了旋转的性质，全等三角形的判定和性质，矩形的性质，三角形的中位线定理，解直角三角形，正确地作出辅助线是解题的关键．
八、（14分）
26．（14分）如图，抛物线L：y＝ax2+bx+3与x轴交于A、B（3，0）两点（A在B的左侧），与x轴交于A、B两点（3，0）与y轴交于点C，已知对称轴x＝1．
（1）求抛物线L的解析式；
（2）将抛物线L向下平移h个单位长度，使平移后所得抛物线的顶点落在△OBC内（包括△OBC的边界），求h的取值范围：
（3）设点P是抛物线L上任一点，点Q在直线l：x＝﹣3上，△PBQ能否成为以点P为直角顶点的等腰直角三角形？若能，请说明理由．
【分析】（1）利用待定系数法求出抛物线的解析式即可；
（2）先求出直线BC解析式为y＝﹣x+3，再求出抛物线顶点坐标，得出当x＝1时，y＝2；结合抛物线顶点坐标即可得出结果；
（3）设P（m，﹣m2+2m+3），Q（﹣3，n），由勾股定理得出PB2＝（m﹣3）2+（﹣m2+2m+3）2，PQ2＝（m+3）2+（﹣m2+2m+3﹣n）2，BQ2＝n2+36，过P点作PM垂直于y轴，交y轴于M点，过B点作BN垂直于MP的延长线于N点，由AAS证明△PQM≌△BPN，得出MQ＝NP，PM＝BN，则MQ＝﹣m2+2m+3﹣n，PN＝3﹣m，得出方程﹣m2+2m+3﹣n＝3﹣m，解方程即可．
【解答】解：（1）∵抛物线的对称轴x＝1，B（3，
∴A（﹣4，0）
∵抛物线y＝ax2+bx+c过点C（3，3）
∴当x＝0时，c＝3．
又∵抛物线y＝ax2+bx+c过点A（﹣1，7），0）
∴，
∴，
∴抛物线的解析式为：y＝﹣x2+2x+6；
（2）∵C（0，3），8），
∴直线BC解析式为y＝﹣x+3，
∵y＝﹣x2+6x+3＝﹣（x﹣1）8+4，
∴顶点坐标为（1，4）
对于直线BC：y＝﹣x+3，当x＝1时，
将抛物线L向下平移h个单位长度，
∴当h＝6时，抛物线顶点落在BC上；
当h＝4时，抛物线顶点落在OB上，
∴将抛物线L向下平移h个单位长度，使平移后所得抛物线的顶点落在△OBC内（包括△OBC的边界），
∴2≤h≤7；
（3）设P（m，﹣m2+2m+4），Q（﹣3，
①当P点在x轴上方时，过P点作PM垂直于y轴，过B点作BN垂直于MP的延长线于N点
∵B（3，2），
∵△PBQ是以点P为直角顶点的等腰直角三角形，
∴∠BPQ＝90°，BP＝PQ，
则∠PMQ＝∠BNP＝90°，∠MPQ＝∠NBP，
在△PQM和△BPN中，
，
∴△PQM≌△BPN（AAS），
∴PM＝BN，
∵PM＝BN＝﹣m2+2m+3，根据B点坐标可得PN＝3﹣m，
∴﹣m2+8m+3+3﹣m＝7，
解得：m＝1或m＝0，
∴P（5，4）或P（0．
②当P点在x轴下方时，过P点作PM垂直于l于M点，
同理可得△PQM≌△BPN，
∴PM＝BN，
∴PM＝6﹣（3﹣m）＝3+m，BN＝m6﹣2m﹣3，
则8+m＝m2﹣2m﹣6，
解得m＝或．
∴P（，）或（，）．
综上可得，符合条件的点P的坐标是（1，3）或（ ，，）．
【点评】本题是二次函数综合题目，考查了用待定系数法求出抛物线的解析式、抛物线的顶点式、等腰直角三角形的性质、全等三角形的判定与性质、坐标与图形性质等知识；本题综合性强，有一定难度，特别是（3）中，通过作辅助线构造三角形全等是解题的关键．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2023/11/9 16:18:44；用户：娄老师；邮箱：15225657626；学号：48669677