2024届新高考一轮复习函数与导数专练（2）函数的基本性质

这是一份2024届新高考一轮复习函数与导数专练（2）函数的基本性质，共4页。试卷主要包含了函数在区间上，已知函数，且，则，已知若为上的奇函数，，则，函数的图像大致为等内容，欢迎下载使用。
1.函数在区间上( )
A.单调递增B.单调递减C.先减后增D.先增后减
2.如图，在直角梯形OABC中，，，，直线截该梯形所得的位于l左边的图形面积为S，则函数的图象大致为( ).
A.B.C.D.
3.函数是定义在R上的单调函数，，则( )
A.9B.8C.3D.1
4.已知函数，且，则( )
A.-7B.7C.3D.-2
5.已知若为上的奇函数，，则( )
A.B.C.D.-1
6.规定表示取a，b中的较大者，如，，则函数的最小值为( )
A.1B.2C.3D.4
7.已知函数的定义域为R，为奇函数，为偶函数，则( )
A.B.C.D.
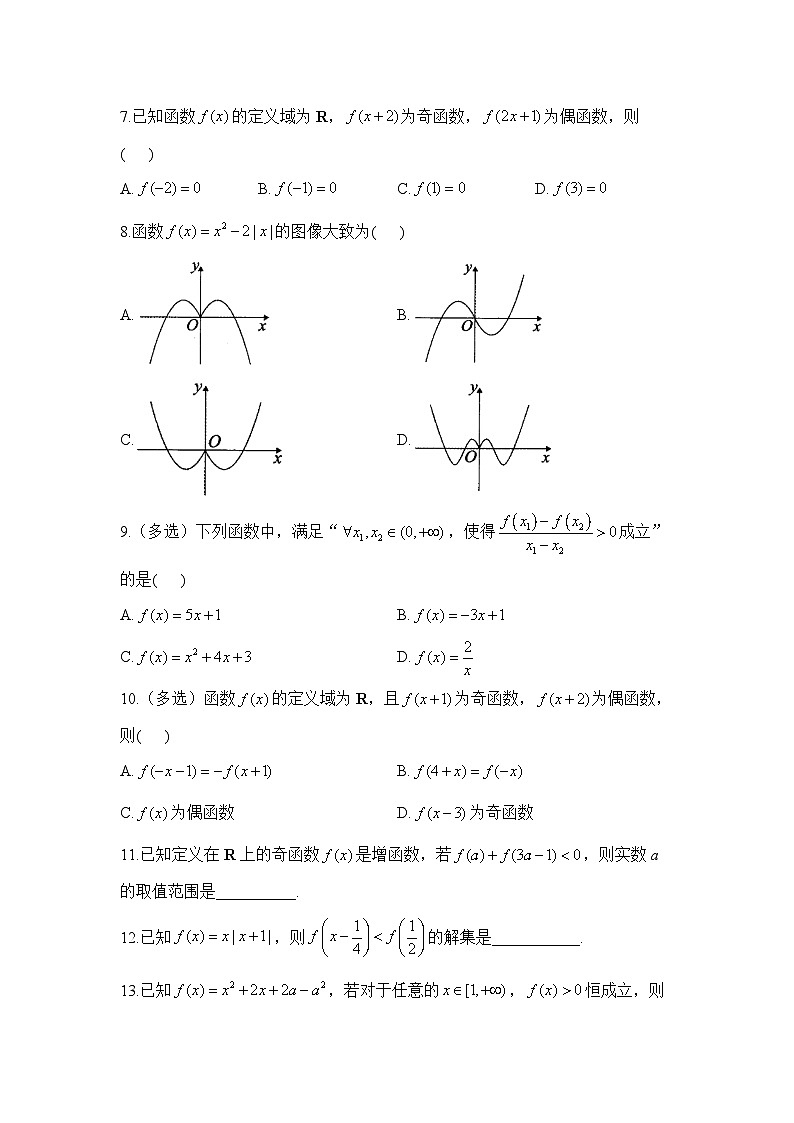
8.函数的图像大致为( )
A.B.
C.D.
9.（多选）下列函数中，满足“，使得成立”的是( )
A.B.
C.D.
10.（多选）函数的定义域为R，且为奇函数，为偶函数，则( )
A.B.
C.为偶函数D.为奇函数
11.已知定义在R上的奇函数是增函数，若，则实数a的取值范围是__________.
12.已知，则的解集是___________.
13.已知，若对于任意的，恒成立，则实数a的取值范围为___________.
14.已知是定义域为R的奇函数，且为偶函数.若，则__________.
15.定义在R上的单调函数满足恒等式，且.
（1）求，；
（2）判断函数的奇偶性，并证明；
（3）若对于任意都有成立，求实数k的取值范围.
答案以及解析
1.答案：C
解析：函数的图像开口向上，其对称轴为直线，所以该函数在区间上单调递减，在区间上单调递增.故选C.
2.答案：C
解析：
3.答案：C
解析：因为函数是定义在R上的单调函数，且，所以为常数.记，则，，所以.不妨设函数单调递增，且，则，即（矛盾），故.所以，故.选C.
4.答案：C
解析：由函数，令，则，，所以，故是奇函数，所以，则，所以.故选C.
5.答案：C
解析：由题意得，当时，.因为为上的奇函数，所以，所以，即，所以（舍去）或.因为，所以.故选C.
6.答案：B
解析：当，即时，；当，即时，.所以显然在上单调递减，在上单调递增，所以当时，取得最小值，最小值为.故选B.
7.答案：A
解析：为奇函数，的图像关于点对称，.为偶函数，的图像关于直线对称，是周期为4的函数，.故选A.
8.答案：C
解析：函数的定义域为R，关于原点对称.由，得，所以函数为偶函数，故排除B.当时，，则函数在上单调递减，在上单调递增，故排除A，D.选C.
9.答案：AC
解析：因为，都有，所以函数在上单调递增.在上单调递增，所以A符合题意；在上单调递减，所以B不符合题意；因为图像的对称轴为直线，且其图像开口向上，所以函数在上单调递增，所以C符合题意；在上单调递减，所以D不符合题意.故选AC.
10.答案：BCD
解析：因为为奇函数，为偶函数，所以的图像关于点对称，同时关于直线对称，所以，A错误；，，B正确；，即函数为周期函数，周期为4，所以，即函数为偶函数，C正确；，所以函数为奇函数，D正确.故选BCD.
11.答案：
解析：因为函数为奇函数，所以由，得.又函数在R上为增函数，所以，解得.
12.答案：
解析：由图象可知，等价于，即.
13.答案：
解析：设.，.要使在上恒成立，只需在上的最小值大于即可.在上单调递增，，，解得.实数a的取值范围是.
14.答案：1
解析：因为是定义域为R的奇函数，且为偶函数，所以，且，即，所以，所以是周期函数，周期为4.因为，，，，所以
.
15.答案：（1），
（2）函数是奇函数
（3）实数k的取值范围为
解析：（1）令，得.
令，，得，
，.
（2）函数是奇函数.证明如下.
令，得，
，即，
函数是奇函数.
（3）因为是奇函数，且在上恒成立，
在上恒成立.
是定义域在R上的单调函数，且，
是R上的增函数，
，
即在上恒成立，
在上恒成立.
令.
，.
由抛物线的图像，得，.
故实数k的取值范围为.