山东省泰安市岱岳区黄前中学2023-2024学年上学期期中考试七年级数学试题

这是一份山东省泰安市岱岳区黄前中学2023-2024学年上学期期中考试七年级数学试题，共6页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。

时间：120分钟 满分：150分
一、选择题（每小题3分，共48分）
1．我国主要银行的商标设计基本上都融入了中国古代钱币的图案，如图是我国四个银行的商标图案，其中是轴对称图形的有（ ）
A．①②③B．①②④C．①③④D．②③④
2．如图，AB∥DF，且AB＝DF，添加下列条件，不能判断△ABC≌△FDE的是（ ）
A．AC＝EFB．BE＝CDC．AC∥EFD．∠A＝∠F
3．按下列各组数据能组成直角三角形的是（ ）
A．11，15，13B．1，4，5C．8，15，17 D．4，5，6
如图，将含有30°角的三角板的直角顶点放在平行的两条直线其中一条上，若∠1=35°，∠2的度数为（ ）
A．10° B．20° C．25° D．30°
第4题 第5题 第6题
5.“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b，若(a+b)2=21，大正方形的面积为13，则小正方形的面积为( )
3B. 4C. 5D. 6
6.如图，在△ABC中，AC=4cm，线段AB的垂直平分线交AB，AC于点M，N，△BCN的周长是7cm，则BC的长为( )
A. 4cmB. 3cmC. 2cmD. 1cm
7.如图，在长方形纸片ABCD中，AB=8cm，AD=6cm.把长方形纸片沿直线AC折叠，点B落在点E处，AE交DC于点F，则AF的长为( )
254cm B. 152cm C. 7cm D. 132cm
8.如图，在△ABC中，∠A=50°，∠B=∠C，点D，E，F分别在边BC，CA，AB上，且满足BF=CD，BD=CE，∠BFD=30°，则∠FDE的度数为( )
75°B. 80°C. 65°D. 95°
第7题 第8题 第9题 第10题
9.如图，有一个水池，水面是边长为8尺的正方形，在水池中央有一根芦苇，它高出水面1尺，如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面，这根芦苇的长度是( )
7.5尺B. 8尺C. 8.5尺D. 9尺
10.如图，在5×5的正方形网格中，从在格点上的点A，B，C，D中任取三点，所构成的三角形恰好是直角三角形的个数为( )
A. 1 B. 2 C. 3 D. 4
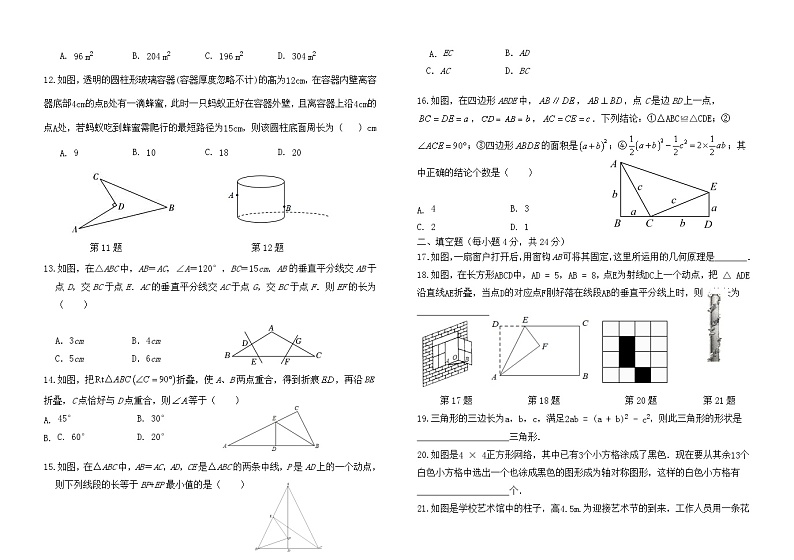
11.如图所示的一块地，已知∠ADC=90°，AD=12 m，CD=9 m，AB=25 m，BC=20 m，则这块地的面积为( )
A. 96 m2B. 204 m2C. 196 m2D. 304 m2
12.如图，透明的圆柱形玻璃容器(容器厚度忽略不计)的高为12cm，在容器内壁离容器底部4cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在容器外壁，且离容器上沿4cm的点A处，若蚂蚁吃到蜂蜜需爬行的最短路径为15cm，则该圆柱底面周长为（ ）cm
9B. 10C. 18D. 20
第11题 第12题
13.如图，在△ABC中，AB＝AC，∠A＝120°，BC＝15cm．AB的垂直平分线交AB于点D，交BC于点E．AC的垂直平分线交AC于点G，交BC于点F．则EF的长为（ ）
A．3cmB．4cm
C．5cmD．6cm
14.如图，把折叠，使A、B两点重合，得到折痕，再沿折叠，C点恰好与D点重合，则等于（ ）
45°B. 30°
C. 60°D. 20°
15.如图，在△ABC中，AB＝AC，AD，CE是△ABC的两条中线，P是AD上的一个动点，则下列线段的长等于BP+EP最小值的是（ ）
ECB．AD
C．ACD．BC
16.如图，在四边形ABDE中，，，点C是边BD上一点，，，．下列结论：①△ABC≌△CDE；②；③四边形的面积是；④；其中正确的结论个数是（ ）

4B. 3
C. 2D. 1
二、填空题（每小题4分，共24分）
17．如图，一扇窗户打开后，用窗钩AB可将其固定，这里所运用的几何原理是 ．
18.如图，在长方形ABCD中，AD=5，AB=8，点E为射线DC上一个动点，把△ADE沿直线AE折叠，当点D的对应点F刚好落在线段AB的垂直平分线上时，则DE的长为 ．
第17题 第18题 第20题 第21题
19.三角形的三边长为a，b，c，满足2ab=(a+b)2-c2，则此三角形的形状是 三角形．
20.如图是4×4正方形网络，其中已有3个小方格涂成了黑色．现在要从其余13个白色小方格中选出一个也涂成黑色的图形成为轴对称图形，这样的白色小方格有 个．
21.如图是学校艺术馆中的柱子，高4.5m.为迎接艺术节的到来，工作人员用一条花带从柱底向柱顶均匀地缠绕3圈，一直缠到起点的正上方为止．若柱子的底面周长是2m，则这条花带至少需要______m.
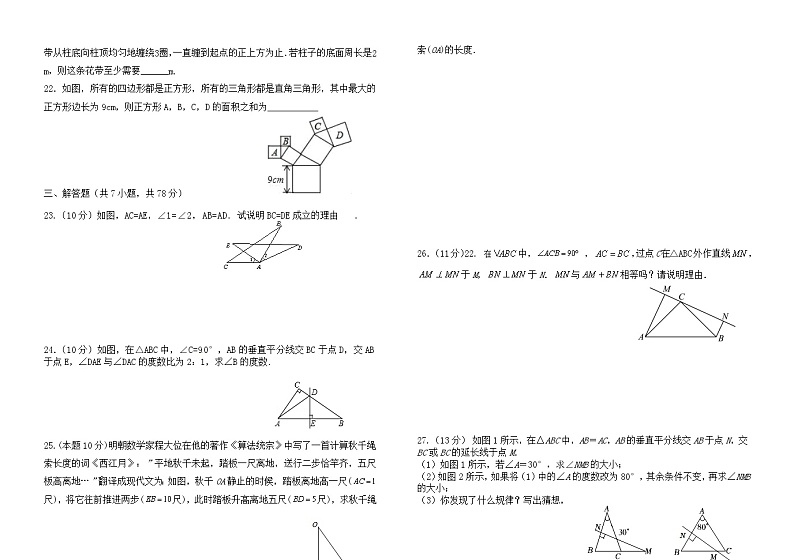
22．如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形边长为9cm，则正方形A，B，C，D的面积之和为
解答题（共7小题，共78分）
23.（10分）如图，AC=AE，∠1=∠2，AB=AD. 试说明BC=DE成立的理由.
（10分）如图，在△ABC中，∠C=90°，AB的垂直平分线交BC于点D，交AB于点E，∠DAE与∠DAC的度数比为2：1，求∠B的度数．
25.(本题10分)明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》：”平地秋千未起，踏板一尺离地，送行二步恰竿齐，五尺板高离地…”翻译成现代文为：如图，秋千OA静止的时候，踏板离地高一尺(尺)，将它往前推进两步(尺)，此时踏板升高离地五尺(尺)，求秋千绳索(OA)的长度．
26．（11分）22. 中， ，，过点C在△ABC外作直线，于M，于N．与相等吗？请说明理由．
27.（13分） 如图1所示，在△ABC中，AB＝AC，AB的垂直平分线交AB于点N，交BC或BC的延长线于点M．
（1）如图1所示，若∠A＝30°，求∠NMB的大小；
（2）如图2所示，如果将（1）中的∠A的度数改为80°，其余条件不变，再求∠NMB的大小；
（3）你发现了什么规律？写出猜想，
28.(11分)如图，在△ABC中，点是边的中点，连结并延长到点，使，连结．
（1）求证：△ABD≌△ECD；
（2）若△ABD的面积为5，求△ACE的面积
29.（13分）D为等边△ABC的边AC上一点，E为直线AB上一点，CD=BE．
（1）如图1，求证；AD=DE；
（2）如图2，DE交CB于点P．①若DE⊥AC，PC=6，求BP的长；
②猜想PD与PE之间的数量关系，直接写出你的结论，不必证明
参考答案
选择题：
1-5题DACCC 6-10题 BACAC 11-15题 ACCBA 16题 B
填空题:
三角形的稳定性 18、 19、 直角
20、3 21、 7.5 22、 81
解答题
23题
证明：∵∠1=∠2
∴∠1+∠EAB=∠2+∠BAE
即∠CAB=∠EAD
在△ABC和△ADE中
AB=AD
∠CAB=∠EAD
AC=AE
∴△ABC≌△ADE
∴BC=DE
24题，解：
∵DE是AB的垂直平分线
∴DA=DB
∴∠DAB=∠B
∵∠DAE：∠DAC=2:1
设∠DAC=x
则∠DAE=∠B=x
∵∠C=90°
∴∠BAC+∠B=90°
∴x+2x+2x=90°
∴x=18°
∴∠B=2x=36°
25题，解：
根据题意得：AC=1尺，EB=10尺，BD=5尺，AE=BD-AC=4C尺
设 OA=OA=x
则OE=OA-AE=x-4
在△OEB中∠OEB=90°
∴OE2+BE2=OB2
∴（x-4）2+100=x2
解得：x=14.5
所以秋千绳索的长度是14.5尺。
26题
MN=AM+BN
理由是：
∵AM⊥MN，BN⊥MN
∴∠AMC=∠BNC=90°
∴∠MAC+∠ACM=90°
∵∠ACB=90°
∴∠ACM+∠BCN=90
∴∠MAC=∠BCN
在△MAC和△NCB中
∠MAC=∠BCN
AC=BC
∠AMC=∠BNC
∴△MAC≌△NCB
∴AM=CN,CM=BN
∵MN=MC+CN
∴MN=AM+BN
27题
∵AB=AC
∴∠B=∠ACB
∵∠A+∠B+∠ACB=180°
∠A=30°
∴∠B=75°
∵MN⊥AB
∴∠MNB=90°
∴∠NMB=90°-75°=15°
（2）∵AB=AC
∴∠B=∠ACB
∵∠A+∠B+∠ACB=180°
∠A=80°
∴∠B=50°
∵MN⊥AB
∴∠MNB=90°
∴∠NMB=90°-50°=40°
（3）
28题
证明：∵D是BC的中点
∴BD=DC
在△ABD和△ECD中
BD=DC
∠ADB=∠CDE
AD=DE
∴△ABD≌△ECD
（2）∵△ABD≌△ECD
∴S△ECD=S△ABD=5
∵D是BC的中点
∴S△ACO=S△ABD=5
∴S△ACE=S△ECD+S△ACD=10
29题
∵△ABC是等边三角形
∴AB=AC , ∠A=∠C=60°
∵EB=CD
∴AB-EB=AC-CD
即AE=AD
∵∠A=60°
∴△ADE是等边三角形
∴AD=DE
∵ED⊥AC
∴∠PDC=∠EDA=90°
△PCD中，∠PDC=90°∠C=60°
∴∠DPC=30°
∴
△ADE中，∠EDA=90°，∠A=60°
∴∠E=30°
∵∠EPB=∠DPC=30°
∴∠E=∠EPB
∴BP=PE
∵CD=BE=3
∴BP=3
PD=PE