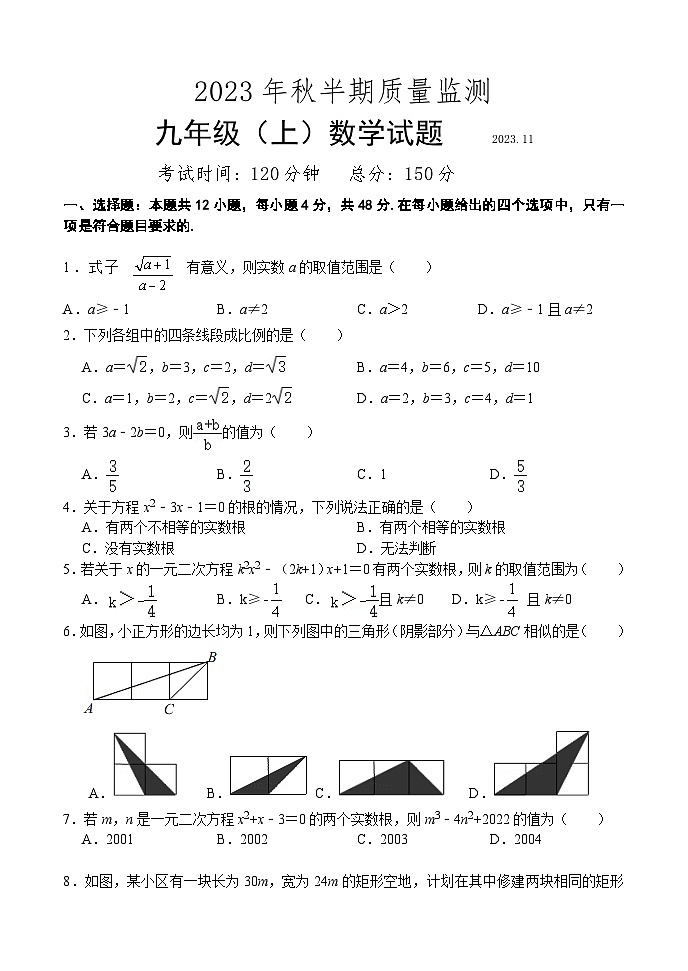
四川省眉山市仁寿县城区2023-2024学年九年级上学期期中考试数学试题

这是一份四川省眉山市仁寿县城区2023-2024学年九年级上学期期中考试数学试题，文件包含23-24学年第一学期期中试卷二-原卷docx、23-24学年第一学期期中试卷二-解析版docx等2份试卷配套教学资源，其中试卷共16页， 欢迎下载使用。

考试时间：120分钟 总分：150分
一、选择题：本题共12小题，每小题4分，共48分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．式子 有意义，则实数a的取值范围是（ ）
A．a≥﹣1B．a≠2C．a＞2 D．a≥﹣1且a≠2
2．下列各组中的四条线段成比例的是（ ）
A．a＝，b＝3，c＝2，d＝B．a＝4，b＝6，c＝5，d＝10
C．a＝1，b＝2，c＝，d＝2D．a＝2，b＝3，c＝4，d＝1
3．若3a﹣2b＝0，则的值为（ ）
A．B．C．1D．
4．关于方程x2﹣3x﹣1＝0的根的情况，下列说法正确的是（ ）
A．有两个不相等的实数根B．有两个相等的实数根
C．没有实数根D．无法判断
5．若关于x的一元二次方程k2x2﹣（2k+1）x+1＝0有两个实数根，则k的取值范围为（ ）
A．B．k≥ C．且k≠0 D．k≥ 且k≠0
6．如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC相似的是（ ）

A． B．C． D．
7．若m，n是一元二次方程x2+x﹣3＝0的两个实数根，则m3﹣4n2+2022的值为（ ）
A．2001B．2002C．2003D．2004
8．如图，某小区有一块长为30m，宽为24m的矩形空地，计划在其中修建两块相同的矩形绿地，两块绿地的面积之和为480m2，两块绿地之间及周边有宽度相等的人行通道，设人行道的宽度为x m，根据题意，下面所列方程正确的是（ ）
A．（30﹣3x）（24﹣2x）＝480B．（30﹣3x）（24﹣x）＝480
C．（30﹣2x）（24﹣2x）＝480D．（30﹣x）（24﹣2x）＝480
9．如图，l1∥l2∥l3，两条直线与这三条平行线分别交于点A、B、C和D、E、F，若，则的值为（ ）
A．B．C．D．
10．如图，直角三角形的直角顶点在坐标原点，AO＝2BO，若点A在反比例函数y＝（x＞0）的图象上，点B在反比例函数y＝（k＜0）的图象上，则k的值是（ ）
A．﹣2B．﹣C．﹣1D．2
11．如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足为点D，如果＝，AD＝9，那么BC的长是（ ）
A．4 B．6 C．2D．3
（第8题图） （第9题图） （第10题图） （第11题图）
12．已知A＝x2+6x+n2，B＝2x2+4x+2n2+3，下列结论正确的个数为（ ）
①若A＝x2+6x+n2是完全平方式，则n＝±3；
②B﹣A的最小值是2；
③若n是A+B＝0的一个根，则；
④若（2022﹣A）（A﹣2019）＝0，则（2022﹣A）2+（A﹣2019）2＝4．
A．1个B．2个C．3个 D．4个
填空题（本题共6个小题，每小题4分，共24分）
13．化简﹣＝ ．
14．已知方程，则的值为 ．
15．如右图，有长为24m的篱笆，现一面利用墙（墙的最大可用长度a为10m）围成中间隔有一道篱笆的长方形花圃，要围成面积为45m2的花圃，AB的长是 ．
16．已知，则k的值是 ；
17．如右图，在平行四边形ABCD中，∠ABC的平分线交AC于点E，交AD于点F，交CD的延长线于点G，若AF＝2FD，则的值为 ．
18．如右图，正方形ABCD中，点F是BC边上一点，连接AF，以AF为对角线作正方形AEFG，边FG与正方形ABCD的对角线AC相交于点H，连接DG．以下四个结论：
①∠EAB＝∠GAD；②△AFC∽△AGD；③2AE2＝AG•AC；④DG⊥AC．
则下列结论正确的有 ．（把正确的番号填在横线上）
三、解答题：（本大题共8个题，共78分）解答应写出文字说明，证明过程或演算步骤：
19.（8分）计算：

20．（8分）用适当的方法解下列方程．
（1）x2﹣2x＝2x+1； （2）（x﹣2）2＝3（2﹣x）；
21．（10分）已知，求的值．
22．（10分）仁寿城区某商场于今年年初以每件25元的进价购进一批商品．当商品售价为40元时，一月份销售256件．二、三月该商品十分畅销．在售价不变的基础上，三月份的销售量达到400件．设二、三这两个月月平均增长率不变．
（1）求二、三这两个月的月平均增长率；
（2）从四月份起，商场决定采用降价促销的方式回馈顾客，经调查发现，该商品每降价2元，销售量增加10件，当商品降价多少元时，商场获利4250元？
23．（10分）已知关于x的一元二次方程x2﹣2（a﹣1）x+a2﹣a﹣2＝0有两个不相等的实
数根x1，x2．
（1）若a为正整数，求a的值；
（2）若x1，x2满足x12+x22﹣x1x2＝16，求a的值．
24．（10分）为了测量学校旗杆的高度AB，数学兴趣小组带着标杆和皮尺来到操场进行测量，测量方案如下：如图，首先，小红在C处放置一平面镜，她从点C沿BC后退，当退行1.8米到D处时，恰好在镜子中看到旗杆顶点A的像，此时测得小红眼睛到地面的距离ED为1.5米；然后，小明在F处竖立了一根高1.6米的标杆FG，发现地面上的点H、标杆顶点G和旗杆顶点A在一条直线上，此时测得FH为2.4米，DF为3.3米，已知AB⊥BH，ED⊥BH，GF⊥BH，点B、C、D、F、H在一条直线上．
（1）求出 的 ；
（2）请根据以上所测数据，计算学校旗杆AB的高度．
25．（10分）如图，在△ABC中，AD是BC边上的中线，且AD＝AC，DE⊥BC，DE与AB相交于点E，EC与AD相交于点F．
（1）求证：△FCD∽△ABC；
（2）过点A作AM⊥BC于点M，求DE：AM的值；
（3）若S△FCD＝10，BC＝16，求DE的长．
26．（12分）如图，已知矩形OABC，以点O为坐标原点建立平面直角坐标系，其中A（2，0），C（0，3），点P以每秒1个单位的速度从点C出发在射线CO上运动，连接BP，作BE⊥PB交x轴于点E，连接PE交AB于点F，设运动时间为t秒．
（1）若AB平分∠EBP，求t的值；
（2）当t＝1时，求点E的坐标；
（3）在运动的过程中，是否存在以P、O、E为顶点的三角形与△ABE相似．若存在，请求出点P的坐标；若不存在，请说明理由．
2023年秋半期质量监测
九年级（上）数学试题参考答案
选择题（本大题共12个小题，每小题4分，共48分）
D 2. C 3. D 4. A 5. D 6. B 7. C 8. A 9. A 10. A 11. C 12.B
填空题（本大题共6个小题，每小题4分，共24分）
14. 6 15. 5 m
2或-1 17. 18. ①②④
解答题（本大题共8个小题，共78分）
（1）解：原式= -4+3-（-2）+1 2分

=2 4分
1分
2分
解：原式
3分

4分


20. （1）x2﹣4x＝1，
x2﹣4x+4＝5， 1分
（x﹣2）2＝5， 2分
x﹣2＝±， 3分
∴ x1＝2+，x2＝2﹣； 4分
（2）（x﹣2）2＝3（2﹣x），
（x﹣2）2+3（x﹣2）＝0， 1分
（x-2)(x-2+3)=0 2分
x﹣2＝0或x﹣2+3＝0， 3分
∴ x1＝2，x2＝﹣1； 4分
3分
21.解：原式
5分

7分
8分
9分
10分

22.解：（1）设二、三这两个月的月平均增长率为x，根据题意可得： 1分
256（1+x）2＝400， 3分
解得：x1＝，x2＝﹣（不合题意舍去）． 4分
答：二、三这两个月的月平均增长率为25%； 5分
（2）设当商品降价m元时，商品获利4250元，根据题意可得： 6分
（40﹣25﹣m）（400+5m）＝4250， 8分
解得：m1＝5，m2＝﹣70（不合题意舍去）． 9分
答：当商品降价5元时，商品获利4250元． 10分
23.解：（1）∵关于x的一元二次方程x2﹣2（a﹣1）x+a2﹣a﹣2＝0有两个不相等的实数根，
2分
∴Δ＝[﹣2（a﹣1）]2﹣4（a2﹣a﹣2）＞0，
3分
解得：a＜3，
4分
∵a为正整数，
∴a＝1，2；
5分
（2）∵x1+x2＝2（a﹣1），x1x2＝a2﹣a﹣2，
7分
∵+﹣x1x2＝16，
∴（x1+x2）2﹣3x1x2＝16，
9分
∴[2（a﹣1）]2﹣3（a2﹣a﹣2）＝16，
解得：a1＝﹣1，a2＝6，
10分
∵a＜3，
∴a＝﹣1．
解：（1）∵∠ABC＝∠CDE＝90°，
2分
∠ACB＝∠DCE，
∴△ACB∽△ECD，
∴，
∵DE＝1.5米，CD＝1.8米，
5分
∴＝＝，
，
（2）∵FG⊥BH，AB⊥BH，
∴AB∥FG，
7分
∴△HFG∽△HBA，
∴＝，
10分
9分
答：学校旗杆AB的高度为25米．
25.（1）证明：∵D是BC边上的中点，DE⊥BC，
∴EB=EC
1分
∴∠B＝∠DCE，
2分
∵AD＝AC，
3分
∴∠ADC＝∠ACB，
∴△ABC∽△FCD；
（2）解：∵AD＝AC，AM⊥DC，
∴，
4分
∵BD＝DC，
∴，
∵DE⊥BC，AM⊥BC，
5分
∴DE∥AM，
∴△BDE∽△BMA
6分
∴．
（3）过点A作AM⊥BC，垂足是M，
∵△ABC∽△FCD，BC＝2CD，
∴，
∵S△FCD＝10，
∴S△ABC＝40，又BC＝16，
8分
∴AM＝5；
∵DE∥AM，
∴，
∵，BM＝BD+DM＝12，，
10分
∴．
解：（1）当AB平分∠EBP时，
∠PBF＝45°，
则∠CBP＝∠CPB＝45°，
3分
，
∴t＝2；
（2）∵A(2,0)，C(0,3)
∴OA=2，OC=3
∵四边形OABC是矩形
∴AB=OC=3，BC=OA=2
∠OCB=∠CBA=∠OAB=900
∴∠CBP+∠PBA=900
∵BE⊥BP
∴∠PBA+∠ABE=900
∴∠CBP=∠ABE
5分
∴△CPB∽△AEB
7分
（3）存在，
∵∠ABE+∠ABP＝90°，
∠PBC+∠ABP＝90°，
∴∠ABE＝∠PBC，
∵∠BAE＝∠BCP＝90°，
∴△BCP∽△BAE，
∴，
∴，
8分
∴，
当点P在点O上方时，
若＝时，△POE∽△EAB，
∵OP＝3﹣t，OE＝2+t，
∴＝，
∴t1＝，
t2＝（舍去），
9分
∴OP＝3﹣＝，
∴P的坐标为（0，），
当点P在点O下方时，
①若＝，
则△OPE∽△ABE，
＝，
解得：t1＝3+，t2＝3﹣（舍去），
10分
OP＝t﹣3＝3+﹣3＝，
P的坐标为（0，﹣），
②若＝，
则△OEP∽△ABE，＝，
11分
解得：t2＝﹣9，
∴这种情况不成立，
∴P的坐标为：
12分
（0，），（0，﹣）．