

广东省东莞市可园中学2023-2024学年八年级上学期期中数学试卷
展开
这是一份广东省东莞市可园中学2023-2024学年八年级上学期期中数学试卷,共10页。
A.赛艇B.电子竞技
C.体操D.柔术
2.(3分)点(﹣3,2)关于x轴的对称点是( )
A.(﹣3,﹣2)B.(3,2)C.(﹣3,2)D.(3,﹣2)
3.(3分)以下各组线段为边,能组成三角形的是( )
A.2cm,4cm,6cmB.8cm,6cm,4cm
C.14cm,6cm,7cmD.2cm,3cm,6cm
4.(3分)如图,在△ABC中,点D在CB的延长线上,∠A=70°,∠C=50°,则∠ABD等于( )
A.100°B.110°C.120°D.130°
5.(3分)在Rt△ABC中,∠A=90°,∠C=30°,AB=3,则BC的长是( )
A.6B.4C.3D.2
6.(3分)如图,在等腰△ABC中,AB=AC,∠B=25°,AD是△ABC的中线,则∠BAD的度数是( )
A.72°B.65°C.50°D.36°
7.(3分)如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件,这个条件可以是( )
A.∠B=∠EB.∠BCA=∠FC.BC∥EFD.AD=DC
8.(3分)如图,有A、B、C三个居民小区,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
A.AC、BC两边高线的交点处
B.AC、BC两边垂直平分线的交点处
C.AC、BC两边中线的交点处
D.∠A、∠B两内角平分线的交点处
9.(3分)如图,四边形ABCD中,AD=CD,AB=CB,我们把这种两组邻边分别相等的四边形叫做“筝形”.下列关于“筝形”的结论正确的是( )
A.对角线AC、BD互相垂直平分
B.对角线BD平分∠ABC,∠ADC
C.直线AC、BD是筝形的两条对称轴
D.筝形的面积等于对角线AC,BD的乘积
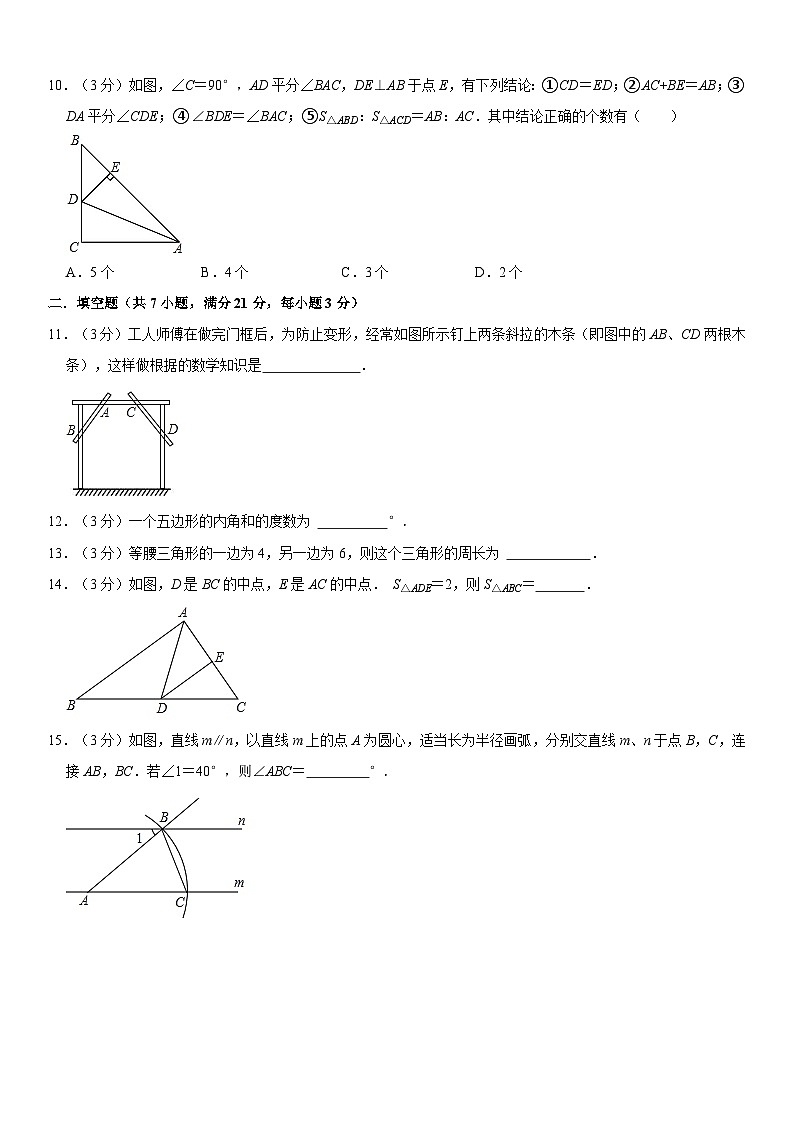
10.(3分)如图,∠C=90°,AD平分∠BAC,DE⊥AB于点E,有下列结论:①CD=ED;②AC+BE=AB;③DA平分∠CDE;④∠BDE=∠BAC;⑤S△ABD:S△ACD=AB:AC.其中结论正确的个数有( )
A.5个B.4个C.3个D.2个
二.填空题(共7小题,满分21分,每小题3分)
11.(3分)工人师傅在做完门框后,为防止变形,经常如图所示钉上两条斜拉的木条(即图中的AB、CD两根木条),这样做根据的数学知识是 .
12.(3分)一个五边形的内角和的度数为 °.
13.(3分)等腰三角形的一边为4,另一边为6,则这个三角形的周长为 .
14.(3分)如图,D是BC的中点,E是AC的中点. S△ADE=2,则S△ABC= .
15.(3分)如图,直线m∥n,以直线m上的点A为圆心,适当长为半径画弧,分别交直线m、n于点B,C,连接AB,BC.若∠1=40°,则∠ABC= °.
16.(3分)将含30°角的直角三角板和直尺按如图所示的方式放置,已知∠α=60°,点B,C表示的刻度分别为1cm,3cm,则线段AB的长为 cm.
17.(3分)如图,等腰△ABC的面积是12,AB=AC,BC=4,EF垂直平分AB,点D为BC的中点,点M为线段EF上一点,则△BDM的周长的最小值为 .
三.解答题(共8小题,满分69分)
18.(6分)一个正多边形的所有内角与它的所有外角之和是1620°,求该正多边形的边数及一个外角的度数.
19.(6分)如图,点D在AB上,E在AC上,AB=AC,∠B=∠C,求证:AD=AE.
20.(6分)如图,在△ABC中,∠C=90°.
(1)尺规作图:作斜边AB的垂直平分线DE,分别交AB,BC于D、E(不写作法,保留作图痕迹);
(2)已知AC=6cm,CB=8cm,求△ACE的周长.
21.(9分)如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE于F,
(1)求∠ACE的度数;
(2)求∠CDF的度数.
22.(9分)如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)△ABC的面积为 ;
(2)请画出△ABC关于y轴对称的△A1B1C1,三个顶点坐标分别A1,B1,C1;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标(保留痕迹).
23.(9分)如图,在△ABC中,BE平分∠ABC交AC于点E,DE∥BC.
(1)求证:△BDE是等腰三角形;
(2)若∠A=50°,∠ABE=30°,求∠AED的大小.
24.(12分)如图,∠BAC的角平分线与线段BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为点E、F.
(1)求证:BE=CF;
(2)求证:AB﹣AC=2BE.
25.(12分)如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
①求证:BE=AD;
②求证:CF=CH;
③判断FH与BD的位置关系,并证明.
广东省东莞市可园中学2023-2024学年八年级上学期数学期中试卷(答案)
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)杭州亚运会将于2023年9月23日举行,下面是杭州亚运会比赛项目中几个项目的图标,其图案可看作轴对称图形的是( )
A.赛艇B.电子竞技
C.体操D.柔术
【解答】解:A,C,D选项中的图形都不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
B选项中的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:B.
2.(3分)点(﹣3,2)关于x轴的对称点是( )
A.(﹣3,﹣2)B.(3,2)C.(﹣3,2)D.(3,﹣2)
【解答】解:点(﹣3,2)关于x轴的对称点的坐标是:(﹣3,﹣2).
故选:A.
3.(3分)以下各组线段为边,能组成三角形的是( )
A.2cm,4cm,6cmB.8cm,6cm,4cm
C.14cm,6cm,7cmD.2cm,3cm,6cm
【解答】解:A、2+4=6,不能组成三角形;
B、4+6=10>8,能组成三角形;
C、6+7=13<14,不能够组成三角形;
D、2+3=5<6,不能组成三角形.
故选:B.
4.(3分)如图,在△ABC中,点D在CB的延长线上,∠A=70°,∠C=50°,则∠ABD等于( )
A.100°B.110°C.120°D.130°
【解答】解:∵∠ABD是△ABC的外角,∠A=70°,∠C=50°,
∴∠ABD=∠A+∠C=70°+50°=120°.
故选:C.
5.(3分)在Rt△ABC中,∠A=90°,∠C=30°,AB=3,则BC的长是( )
A.6B.4C.3D.2
【解答】解:∵∠A=90°,∠C=30°,AB=3,
∴BC=2AB=6,
故选:A.
6.(3分)如图,在等腰△ABC中,AB=AC,∠B=25°,AD是△ABC的中线,则∠BAD的度数是( )
A.72°B.65°C.50°D.36°
【解答】解:∵AB=AC,AD是△ABC的中线,
∴AD⊥BC,
∴∠ADB=90°,
∵∠B=25°,
∴∠BAD=90°﹣25°=65°,
故选:B.
7.(3分)如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件,这个条件可以是( )
A.∠B=∠EB.∠BCA=∠FC.BC∥EFD.AD=DC
【解答】解:A、由∠B=∠E,根据AB=DE,BC=EF能推出△ABC≌△DEF,正确,符合题意;
B、∠BCA=∠F,根据AB=DE,BC=EF和∠BCA=∠F不能推出△ABC≌△DEF,错误,不符合题意;
C、由BC∥EF可得∠BCA=∠EFD,根据AB=DE,BC=EF和∠BCA=∠EFD,不能得出△ABC≌△DEF,错误,不符合题意;
D、根据AB=DE,BC=EF和AD=DC不能推出△ABC≌△DEF,错误,不符合题意.
故选:A.
8.(3分)如图,有A、B、C三个居民小区,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
A.AC、BC两边高线的交点处
B.AC、BC两边垂直平分线的交点处
C.AC、BC两边中线的交点处
D.∠A、∠B两内角平分线的交点处
【解答】解:根据线段垂直平分线上的点到线段两个端点的距离相等,超市应建在边AC和BC的垂直平分线上,
故选:B.
9.(3分)如图,四边形ABCD中,AD=CD,AB=CB,我们把这种两组邻边分别相等的四边形叫做“筝形”.下列关于“筝形”的结论正确的是( )
A.对角线AC、BD互相垂直平分
B.对角线BD平分∠ABC,∠ADC
C.直线AC、BD是筝形的两条对称轴
D.筝形的面积等于对角线AC,BD的乘积
【解答】解:∵AD=CD,
∴点D在线段AC的垂直平分线上,
∵AB=CB,
∴点B在线段AC的垂直平分线上,
∴BD是AC的垂直平分线,
∴筝形的两条对角线互相垂直.故A选项错误;
在△ADB和△CDB中,
AD=CD,AB=CB,BD=BD,
∴△ADB≌△CDB(SSS),
∴∠ADB=∠CDB,∠ABD=∠CBD,
即对角线BD平分∠ABC,∠ADC,故B选项正确;
直线BD是筝形的对称轴,AC不是,故C选项错误;
筝形的面积=S△ABD+S△ACD=,即筝形的面积等于对角线AC,BD的乘积的一半,故D选项错误.
故选:B.
10.(3分)如图,∠C=90°,AD平分∠BAC,DE⊥AB于点E,有下列结论:①CD=ED;②AC+BE=AB;③DA平分∠CDE;④∠BDE=∠BAC;⑤S△ABD:S△ACD=AB:AC.其中结论正确的个数有( )
A.5个B.4个C.3个D.2个
【解答】解:∵在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,
∴CD=ED,①正确;
在Rt△ADE和Rt△ADC中,,
∴Rt△ADE≌Rt△ADC(HL),
∴∠ADE=∠ADC,AE=AC,
即AD平分∠CDE,③正确;
∵AE=AC,
∴AB=AE+BE=AC+BE,②正确;
∵∠BDE+∠B=90°,∠B+∠BAC=90°,
∴∠BDE=∠BAC,④正确;
∵S△ABD=AB•DE,S△ACD=AC•CD,
∵CD=ED,
∴S△ABD:S△ACD=AB:AC,⑤正确.
结论正确的个数有5个,
故选:A.
二.填空题(共7小题,满分21分,每小题3分)
11.(3分)工人师傅在做完门框后,为防止变形,经常如图所示钉上两条斜拉的木条(即图中的AB、CD两根木条),这样做根据的数学知识是 三角形的稳定性 .
【解答】解:这样做根据的数学知识是:三角形的稳定性.
12.(3分)一个五边形的内角和的度数为 540 °.
【解答】解:(5﹣2)•180°=540°,
所以一个五边形的内角和的度数为540°.
故答案为:540.
13.(3分)等腰三角形的一边为4,另一边为6,则这个三角形的周长为 14或16 .
【解答】解:①当腰长为4时,
则三角形的三边长为:4、4、6;
∵4+4>6,
∴能构成三角形,
∴这个等腰三角形的腰长为4,则其周长=6+4+4=14;
②当腰长为6时,
则三角形的三边长为:4、6、6,
∵6+4>6,
∴能构成三角形;
因此这个等腰三角形的腰长为6,则其周长=6+6+4=16,
综上所述,这个等腰三角形的周长为14或16,
故答案为:14或16.
14.(3分)如图,D是BC的中点,E是AC的中点. S△ADE=2,则S△ABC= 8 .
【解答】解:∵E是AC的中点,
∴S△ACD=2S△ADE=2×2=4,
∵D是BC的中点,
∴S△ABC=2S△ACD=2×4=8.
故答案为:8.
15.(3分)如图,直线m∥n,以直线m上的点A为圆心,适当长为半径画弧,分别交直线m、n于点B,C,连接AB,BC.若∠1=40°,则∠ABC= 70 °.
【解答】解:∵m∥n,
∴(∠1+∠2)+∠3=180°,
∵AB=AC,
∴∠2=∠3,
∵∠1=40°,
∴40°+2∠2=180°,
解得∠2=70°,
即∠ABC=70°,
故答案为:70.
16.(3分)将含30°角的直角三角板和直尺按如图所示的方式放置,已知∠α=60°,点B,C表示的刻度分别为1cm,3cm,则线段AB的长为 2 cm.
【解答】解:∵直尺的两对边相互平行,
∴∠ACB=∠α=60°,
∵∠A=60°,
∴∠ABC=180°﹣∠ACB﹣∠A=180°﹣60°﹣60°=60°,
∴∠A=∠ABC=∠ACB,
∴△ABC是等边三角形,
∴AB=BC=3﹣1=2(cm).
故答案为:2.
17.(3分)如图,等腰△ABC的面积是12,AB=AC,BC=4,EF垂直平分AB,点D为BC的中点,点M为线段EF上一点,则△BDM的周长的最小值为 8 .
【解答】解:连接AD交EF与点M′,连接AM.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=BC•AD=×4•AD=12,
解得AD=6,
∵EF是线段AB的垂直平分线,
∴AM=BM.
∴BM+MD=MD+AM.
∴当点M位于点M′处时,MB+MD有最小值,最小值6.
∴△BDM的周长的最小值为DB+AD=2+6=8,
故答案为:8.
三.解答题(共8小题,满分69分)
18.(6分)一个正多边形的所有内角与它的所有外角之和是1620°,求该正多边形的边数及一个外角的度数.
【解答】解:设该正多边形的边数为n,
∵一个正多边形的所有内角与它的所有外角之和是1620°,
∴它的边数为(n﹣2)•180°+360°=1620°,
解得:n=9,
即该正多边形的边数为9,
则一个外角的度数为360°÷9=40°,
即该正多边形的边数为9,一个外角的度数为40°.
19.(6分)如图,点D在AB上,E在AC上,AB=AC,∠B=∠C,求证:AD=AE.
【解答】证明:在△ABE与△ACD中,
,
∴△ACD≌△ABE(ASA),
∴AD=AE(全等三角形的对应边相等).
20.(6分)如图,在△ABC中,∠C=90°.
(1)尺规作图:作斜边AB的垂直平分线DE,分别交AB,BC于D、E(不写作法,保留作图痕迹);
(2)已知AC=6cm,CB=8cm,求△ACE的周长.
【解答】解:(1)如图所示,DE即为所求;
(2)∵DE垂直平分AB,
∴AE=BE,
∴△ACE的周长=AC+CE+AE=AC+CE+BE=AC+BC,
又∵AC=6cm,CB=8cm,
∴△ACE的周长=6+8=14(cm).
21.(9分)如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE于F,
(1)求∠ACE的度数;
(2)求∠CDF的度数.
【解答】解:(1)∵∠A=40°,∠B=72°,
∴∠ACB=180°﹣40°﹣72°=68°,
∵CE平分∠ACB,
∴∠ACE=∠BCE=34°;
(2)∵∠CED=∠A+∠ACE=74°,
∴∠CDE=90°,DF⊥CE,
∴∠CDF+∠ECD=∠ECD+∠CED=90°,
∴∠CDF=74°.
22.(9分)如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)△ABC的面积为 3.5 ;
(2)请画出△ABC关于y轴对称的△A1B1C1,三个顶点坐标分别A1,B1,C1;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标(保留痕迹).
【解答】解:(1)△ABC的面积=,
故答案为:3.5;
(2)如图所示:△A1B1C1即为所求,A1(﹣1,1),B1(﹣4,2),C1(﹣3,4),
故答案为:(﹣1,1),(﹣4,2),C1(﹣3,4);
(3)如图所示:点P即为所求,点P的坐标为(2,0).
23.(9分)如图,在△ABC中,BE平分∠ABC交AC于点E,DE∥BC.
(1)求证:△BDE是等腰三角形;
(2)若∠A=50°,∠ABE=30°,求∠AED的大小.
【解答】(1)证明:∵BE平分∠ABC,
∴∠ABE=∠EBC,
∵DE∥BC,
∴∠DEB=∠EBC=∠ABE,
∴BD=ED,
∴△DBE为等腰三角形;
(2)解:∵∠A=50°,∠ABE=30°,
∴∠ABC=2∠ABE=60°,
∴∠C=180°﹣∠A﹣∠ABC=180°﹣50°﹣60°=70°,
∵DE∥BC,
∴∠AED=∠C,
∴∠AED=70°.
24.(12分)如图,∠BAC的角平分线与线段BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为点E、F.
(1)求证:BE=CF;
(2)求证:AB﹣AC=2BE.
【解答】(1)证明:连接CD,
∵DG垂直平分BC,
∴BD=CD,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
在Rt△BDE和Rt△CDF中,
,
∴Rt△BDE≌Rt△CDF(HL),
∴BE=CF;
(2)证明:在Rt△ADE和Rt△ADF中,
,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,
∵AE=AB﹣BE,AF=AC+CF,
∴AB﹣BE=AC+CF,
即AB﹣AC=2BE.
25.(12分)如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
①求证:BE=AD;
②求证:CF=CH;
③判断FH与BD的位置关系,并证明.
【解答】证明:①∵△ABC与△ECD都为等边三角形,
∴AC=BC,EC=DC,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,即∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴AD=BE;
②∵△ACD≌△BCE,
∴∠HAC=∠FBC,
∵∠ACB=∠ECD=60°,
∴∠ACH=60°,
在△ACH和△BCF中,
,
∴△ACH≌△BCF(AAS),
∴CF=CH;
③FH∥BD,理由为:
∵CF=CH,且∠FCH=60°,
∴△CFH为等边三角形,
∴∠HFC=∠ACB=60°,
∴FH∥BD.
相关试卷
这是一份广东省东莞市可园中学2023-2024学年八年级上学期期末数学试卷,共10页。
这是一份广东省东莞市可园中学2023-2024学年八年级上学期期末数学试卷+,共10页。
这是一份49,广东省东莞市可园中学等四校联考2023-2024学年八年级上学期期中数学试题(无答案),共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。








