甘肃省陇南市西和县2023-2024学年八年级上学期期中数学试卷

这是一份甘肃省陇南市西和县2023-2024学年八年级上学期期中数学试卷，共10页。
A．全B．面C．发D．展
2．（3分）如果一个三角形的两边长分别是1和3，则第三边长可能是（ ）
A．1B．2C．3D．4
3．（3分）如图，在△ABC中，∠C＝90°，∠B＝30°，AB＝12，则AC等于（ ）
A．8B．7C．6D．5
4．（3分）正十边形的外角和为（ ）
A．360°B．720°C．1080°D．1440°
5．（3分）平面直角坐标系中的点A（﹣3，2）关于x轴对称的点的坐标是（ ）
A．（3，﹣2）B．（3，2）C．（﹣3，2）D．（﹣3，﹣2）
6．（3分）如图，在△ABC中，AB＝AC，∠ABC＝75°，BD是AC边上的高，则∠ABD的度数为（ ）
A．15°B．30°C．60°D．75°
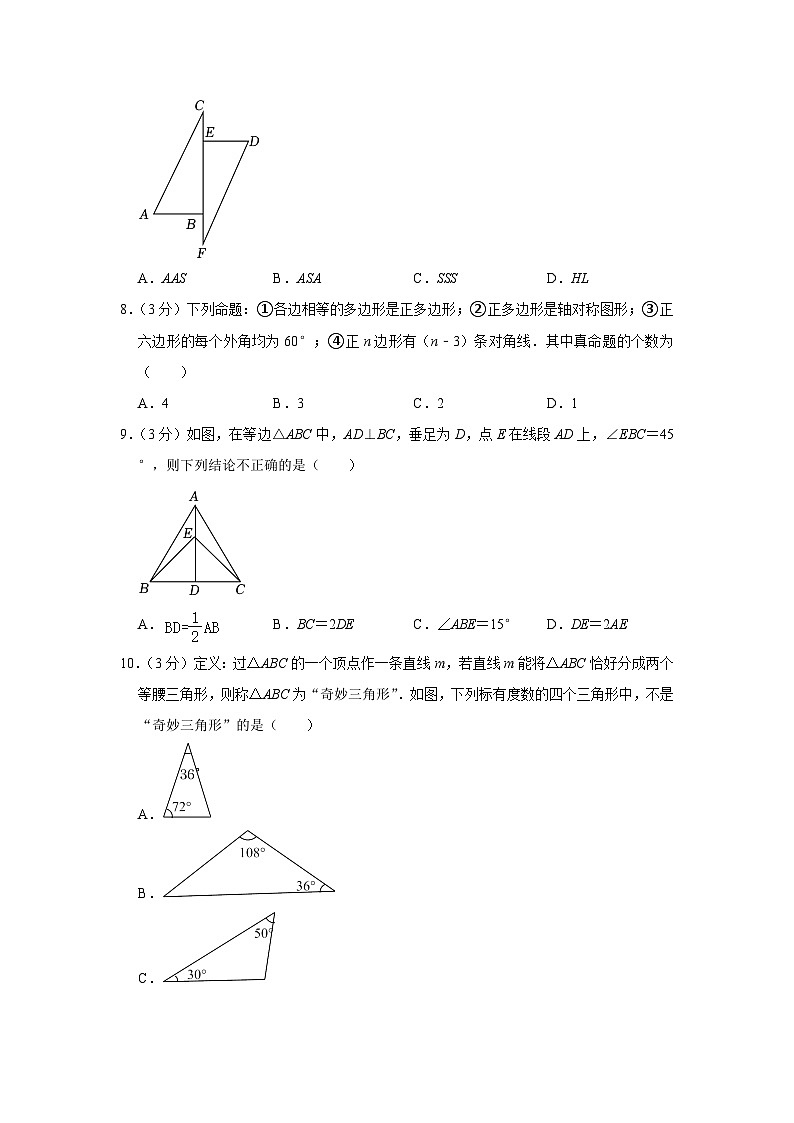
7．（3分）如图，AB⊥CF，垂足为B，DE⊥CF，垂足为E，CB＝FE，AC＝DF，依据上述条件可以判定△ABC≌△DEF，这种判定三角形全等的依据是（ ）
A．AASB．ASAC．SSSD．HL
8．（3分）下列命题：①各边相等的多边形是正多边形；②正多边形是轴对称图形；③正六边形的每个外角均为60°；④正n边形有（n﹣3）条对角线．其中真命题的个数为（ ）
A．4B．3C．2D．1
9．（3分）如图，在等边△ABC中，AD⊥BC，垂足为D，点E在线段AD上，∠EBC＝45°，则下列结论不正确的是（ ）
A．B．BC＝2DEC．∠ABE＝15°D．DE＝2AE
10．（3分）定义：过△ABC的一个顶点作一条直线m，若直线m能将△ABC恰好分成两个等腰三角形，则称△ABC为“奇妙三角形”．如图，下列标有度数的四个三角形中，不是“奇妙三角形”的是（ ）
A．
B．
C．
D．
二.填空题.（每题4分，共24分）
11．（4分）在Rt△ABC中，∠C＝90°，∠B＝56°，则∠A的度数为 ．
12．（4分）如图，点O在一块直角三角板上，OB平分∠ABC，OM⊥AB于点M，ON⊥BC于点N，若OM＝2，则ON＝ ．
13．（4分）如图，在△ABC中，AB＝AC，AD⊥BC于点D，若BC＝6，则CD＝ ．
14．（4分）如图，小明与小红玩跷跷板游戏，如果跷跷板的支点O（即跷跷板的中点）至地面的距离是50cm，当小红从水平位置CD下降40cm时，这时小明离地面的高度是 cm．
15．（4分）如图，在△ABC中，分别以点B和点C为圆心，大于BC长为半径画弧，两弧相交于点M、N．作直线MN，交AC于点D，交BC于点E，连接BD．若AB＝7，AC＝12，BC＝6，则△ABD的周长为 ．
16．（4分）如图，点E在等边△ABC的边BC上，BE＝12，射线CD⊥BC于点C，点P是射线CD上一动点，点F是线段AB上一动点，当EP+PF的值最小时，BF＝14，则AC的长为 ．
三.解答题：本大题6个小题，共46分
17．（6分）如图，OA＝OC，OB＝OD，∠AOD＝∠COB．求证：AB＝CD．
18．（6分）随着新能源共享汽车的普及，某新能源共享汽车公司计划在M区建立一个集中充电点P，按照设计要求：集中充电点P到公路OA、OB的距离相等，并且到两个小区C、D的距离也相等．请在图上标出点P（要求：尺规作图，不写作法，保留作图痕迹）．
19．（6分）如图，∠A＝∠B＝90°，E是AB上的一点，且AD＝BE，∠1＝∠2，求证：Rt△ADE≌Rt△BEC．
20．（8分）如图，在平面直角坐标系中，点O为坐标原点，已知△ABC三个顶点的坐标分别为A（﹣4，1），B（﹣3，3），C（﹣1，2）．画出△ABC关于x轴对称的△A1B1C1，点A、B、C的对称点分别是点A1、B1，C1，直接写出点A1，B1、C1的坐标：A1（ ， ），B1 ， ），C1（ ， ）．
21．（10分）如图，AD＝AB＝BC，AC＝AE，点C在DE上，∠BAD＝∠CAE＝20°．
（1）求∠ACB的度数；
（2）想一想：本题的图形中一共有多少个等腰三角形？为什么？
22．（10分）如图，在△ABC中，∠C＝90°，点D，点E在边BC上，且满足AD＝BD，AE平分∠BAD，若∠CAE＝42°．求∠AEC和∠B的度数．
四.解答题：本大题5小题，共50分
23．（8分）如图，四边形ABCD中，AB∥DC，DB平分∠ADC，∠A＝60°．
求证：△ABD是等边三角形．
24．（10分）如图，在△ABC中，CD是AB边上的高，BE是AC边上的中线，且BD＝CE．求证：
（1）点D在BE的垂直平分线上；
（2）∠BEC＝3∠ABE．
25．（10分）如图，△ABC和△ADE关于直线MN对称，BC与DE的交点F在直线MN上．
（1）图中点C的对应点是点 ，∠B的对应角是 ；
（2）若DE＝5，BF＝2，则CF的长为 ；
（3）若∠BAC＝108°，∠BAE＝30°，求∠EAF的度数．
26．（10分）如图，△ABC中，D为BC上一点，∠ADC＝60°，AE⊥BC于点E，CF⊥AD于点F，AE、CF相交于点G，∠CAE＝15°．
（1）求∠ACF的度数；
（2）求证：．
27．（12分）小明发现这样一个规律：两个顶角相等的等腰三角形，如果具有公共的顶角的顶点，并把它们的底角顶点连接起来，则形成一组全等三角形，小明把具有这个规律的图形称为“手拉手”图形．
（1）问题发现：在图1的“手拉手”图形中，若△ABC和△ADE均是顶角为40°的等腰三角形，BC，DE分别是底边，求证：BD＝CE；
（2）拓展探究：如图2，若△ABC和△CDE均是等边三角形，点A，D，E在同一条直线上，连接BE，则∠AEB＝ °，线段BE与AD之间的数量关系是 ；
（3）解决问题：如图3，若△ABC和△DCE均是等腰直角三角形，∠ACB＝∠DCE＝90°，点A，D，E在同一条直线上，CM为△DCE中DE边上的高，连接BE，请求出∠AEB的度数，写出线段CM，AE，BE之间的数量关系，并说明理由．
2023-2024学年甘肃省陇南州西和县八年级（上）期中数学试卷
（参考答案）
一.选择题.（每题只有一个正确答案，请将正确答案填在下面的表格里.每题3分，共30分）
1．（3分）在一些美术字中，有的汉字是轴对称图形．下面4个汉字中，可以看作是轴对称图形的是（ ）
A．全B．面C．发D．展
【解答】解：全面发展四个字中，可以看作是轴对称图形的是全．
故选：A．
2．（3分）如果一个三角形的两边长分别是1和3，则第三边长可能是（ ）
A．1B．2C．3D．4
【解答】解：设第三边长为x，由题意得：3﹣1＜x＜3+1，
即2＜x＜4，
观察选项，只有选项C符合题意．
故选：C．
3．（3分）如图，在△ABC中，∠C＝90°，∠B＝30°，AB＝12，则AC等于（ ）
A．8B．7C．6D．5
【解答】解：在△ABC中，∠C＝90°，∠B＝30°，AB＝12，
∴AC＝AB＝6．
故选：C．
4．（3分）正十边形的外角和为（ ）
A．360°B．720°C．1080°D．1440°
【解答】解：正十边形的外角和的度数为360°．
故选：A．
5．（3分）平面直角坐标系中的点A（﹣3，2）关于x轴对称的点的坐标是（ ）
A．（3，﹣2）B．（3，2）C．（﹣3，2）D．（﹣3，﹣2）
【解答】解：点A（﹣3，2）关于x轴对称的点的坐标为（﹣3，﹣2），
故选：D．
6．（3分）如图，在△ABC中，AB＝AC，∠ABC＝75°，BD是AC边上的高，则∠ABD的度数为（ ）
A．15°B．30°C．60°D．75°
【解答】解：∵AB＝AC，
∴∠C＝∠ABC＝75°，
∴∠A＝180°﹣∠ABC﹣∠C＝30°，
∵BD⊥AC，
∴∠BDA＝90°，
∴∠ABD＝90°﹣∠A＝60°，
故选：C．
7．（3分）如图，AB⊥CF，垂足为B，DE⊥CF，垂足为E，CB＝FE，AC＝DF，依据上述条件可以判定△ABC≌△DEF，这种判定三角形全等的依据是（ ）
A．AASB．ASAC．SSSD．HL
【解答】解：∵AB⊥CF，垂足为B，DE⊥CF，垂足为E，
∴∠ABC＝∠DEF＝90°，
在Rt△ABC和Rt△DEF中，
，
∴Rt△ABC≌Rt△DEF（HL）．
∴这种判定三角形全等的依据是HL．
故选：D．
8．（3分）下列命题：①各边相等的多边形是正多边形；②正多边形是轴对称图形；③正六边形的每个外角均为60°；④正n边形有（n﹣3）条对角线．其中真命题的个数为（ ）
A．4B．3C．2D．1
【解答】解：①各边相等、各角也相等的多边形是正多边形，故原命题错误，是假命题，不符合题意；
②正多边形是轴对称图形，正确，是真命题，符合题意；
③正六边形的每个外角均为60°，正确，是真命题，符合题意；
④正n边形每个顶点引出有（n﹣3）条对角线，故原命题错误，是假命题，不符合题意．
真命题有2个，
故选：C．
9．（3分）如图，在等边△ABC中，AD⊥BC，垂足为D，点E在线段AD上，∠EBC＝45°，则下列结论不正确的是（ ）
A．B．BC＝2DEC．∠ABE＝15°D．DE＝2AE
【解答】解：∵△ABC为等边三角形，
∴AB＝BC＝AC，∴∠ABC＝∠ACB＝∠BAC＝60°，
∵AD⊥BC，
∴BD＝CD＝BC，
∴BD＝AB，
故选项A正确，不符合题意；
∵AD⊥BC，∠EBC＝45°，
∴△BDE为等腰直角三角形，
∴BD＝DE，
∴DE＝BC，
即BC＝2DE，
故选项B正确，不符合题意；
∵∠ABC＝60°，∠EBC＝45°，
∴∠ABE＝∠ABC﹣∠EBC＝15°，
故选项C正确，不符合题意；
由（1）正确可知：BD＝AB，
∴AB＝2BD，
由勾股定理得：AD＝＝BD，
∵BD＝DE，
∴AE＝AD﹣DE＝DE﹣DE＝（﹣1）DE，
∴选项D不正确，符合题意．
故选：D．
10．（3分）定义：过△ABC的一个顶点作一条直线m，若直线m能将△ABC恰好分成两个等腰三角形，则称△ABC为“奇妙三角形”．如图，下列标有度数的四个三角形中，不是“奇妙三角形”的是（ ）
A．
B．
C．
D．
【解答】解：A．是“奇妙三角形”，不合题意；
B．是“奇妙三角形”，不合题意；
C．不是“奇妙三角形”，符合题意；
D．是“奇妙三角形”，不合题意；
故选：C．
二.填空题.（每题4分，共24分）
11．（4分）在Rt△ABC中，∠C＝90°，∠B＝56°，则∠A的度数为 34° ．
【解答】解：在Rt△ABC中，∠C＝90°，
则∠B+∠A＝90°，
∵∠B＝56°，
∴∠A＝90°﹣56°＝34°．
故答案为：34°．
12．（4分）如图，点O在一块直角三角板上，OB平分∠ABC，OM⊥AB于点M，ON⊥BC于点N，若OM＝2，则ON＝ 2 ．
【解答】解：∵OB平分∠ABC，OM⊥AB于点M，ON⊥BC于点N，
∴ON＝OM＝2．
故答案为：2．
13．（4分）如图，在△ABC中，AB＝AC，AD⊥BC于点D，若BC＝6，则CD＝ 3 ．
【解答】解：∵AB＝AC，AD⊥BC，
∴CD＝BD，
∵BC＝6，
∴CD＝3，
故答案为：3．
14．（4分）如图，小明与小红玩跷跷板游戏，如果跷跷板的支点O（即跷跷板的中点）至地面的距离是50cm，当小红从水平位置CD下降40cm时，这时小明离地面的高度是 90 cm．
【解答】解：在△OCF与△ODG中，，
∴△OCF≌△ODG（AAS），
∴CF＝DG＝40cm，
∴小明离地面的高度是50+40＝90（cm），
故答案为：90．
15．（4分）如图，在△ABC中，分别以点B和点C为圆心，大于BC长为半径画弧，两弧相交于点M、N．作直线MN，交AC于点D，交BC于点E，连接BD．若AB＝7，AC＝12，BC＝6，则△ABD的周长为 19 ．
【解答】解：由题意可得，
MN垂直平分BC，
∴DB＝DC，
∵△ABD的周长是AB+BD+AD，
∴AB+BD+AD＝AB+DC+AD＝AB+AC，
∵AB＝7，AC＝12，
∴AB+AC＝19，
∴△ABD的周长是19，
故答案为：19．
16．（4分）如图，点E在等边△ABC的边BC上，BE＝12，射线CD⊥BC于点C，点P是射线CD上一动点，点F是线段AB上一动点，当EP+PF的值最小时，BF＝14，则AC的长为 20 ．
【解答】解：∵△ABC是等边三角形，
∴AC＝BC，∠B＝60°，
作点E关于直线CD的对称点G，过G作GF⊥AB于F，交CD于P，
则此时，EP+PF的值最小，
∵∠B＝60°，∠BFG＝90°，
∴∠G＝30°，
∵BF＝14，
∴BG＝2BF＝28，
∵BE＝12，
∴EG＝16，
∵CE＝CG＝8，
∴AC＝BC＝20，
故答案为：20．
三.解答题：本大题6个小题，共46分
17．（6分）如图，OA＝OC，OB＝OD，∠AOD＝∠COB．求证：AB＝CD．
【解答】证明：∵∠AOD＝∠COB，
∴∠AOD﹣∠BOD＝∠COB﹣∠BOD，
即∠AOB＝∠COD．
在△AOB 和△COD中，
，
∴△AOB≌△COD（SAS），
∴AB＝CD．
18．（6分）随着新能源共享汽车的普及，某新能源共享汽车公司计划在M区建立一个集中充电点P，按照设计要求：集中充电点P到公路OA、OB的距离相等，并且到两个小区C、D的距离也相等．请在图上标出点P（要求：尺规作图，不写作法，保留作图痕迹）．
【解答】解：如图，点P即为所求．
19．（6分）如图，∠A＝∠B＝90°，E是AB上的一点，且AD＝BE，∠1＝∠2，求证：Rt△ADE≌Rt△BEC．
【解答】证明：∵∠1＝∠2，
∴DE＝CE．
∵∠A＝∠B＝90°，
∴△ADE和△EBC是直角三角形，而AD＝BE．
∴Rt△ADE≌Rt△BEC（HL）
20．（8分）如图，在平面直角坐标系中，点O为坐标原点，已知△ABC三个顶点的坐标分别为A（﹣4，1），B（﹣3，3），C（﹣1，2）．画出△ABC关于x轴对称的△A1B1C1，点A、B、C的对称点分别是点A1、B1，C1，直接写出点A1，B1、C1的坐标：A1（ ﹣4 ， ﹣1 ），B1 （﹣3 ， ﹣3 ），C1（ ﹣1 ， ﹣2 ）．
【解答】解：如图所示，△A1B1C1即为所求，
由图得：A1（﹣4，﹣1），B1（﹣3，﹣3），C1（﹣1，﹣2），
故答案为：﹣4，﹣1，﹣3，﹣3，﹣1，﹣2．
21．（10分）如图，AD＝AB＝BC，AC＝AE，点C在DE上，∠BAD＝∠CAE＝20°．
（1）求∠ACB的度数；
（2）想一想：本题的图形中一共有多少个等腰三角形？为什么？
【解答】解：（1）∵AC＝AE，∠CAE＝20°．
∴∠E＝∠ACE＝（180°﹣20°）＝80°，
∵∠BAD＝∠CAE＝20°．
∴∠BAD+∠CAD＝∠CAE+∠CAD．
∴∠BAC＝∠DAE．
在△ABC和△ADE中，
，
∴△ABC≌△ADE（SAS），
∴∠ACB＝∠E＝80°．
∴∠ACB的度数为80°；
（2）一共有5个等腰三角形，△ABC，△ACE，△ADE，△ABF，△CDF．理由如下：
△ABC为等腰三角形，理由如下：
∵AB＝BC，
∴△ABC为等腰三角形；
△ACE为等腰三角形，理由如下：
∵AC＝AE，
∴△ACE为等腰三角形；
△ADE为等腰三角形，理由如下：
∵△ABC≌△ADE，
∴BC＝DE，
∵AD＝BC，
∴AD＝DE，
∴△ADE为等腰三角形；
△ABF为等腰三角形，理由如下：
∵∠ACB＝80°，AB＝BC，
∴∠BAC＝∠ACB＝80°，
∴∠B＝∠BAD＝20°，
∴AF＝BF，
∴△ABF为等腰三角形；
△CDF为等腰三角形，理由如下：
∵△ABC≌△ADE，∠B＝20°，
∴∠B＝∠D＝20°，
∵∠ACB＝80°，∠ACE＝80°，
∴∠FCD＝180°﹣∠ACB﹣∠ACE＝20°，
∴∠FCD＝∠D＝20°，
∴DF＝CF，
∴△CDF为等腰三角形．
22．（10分）如图，在△ABC中，∠C＝90°，点D，点E在边BC上，且满足AD＝BD，AE平分∠BAD，若∠CAE＝42°．求∠AEC和∠B的度数．
【解答】解：∵∠C＝90°，∠CAE＝42°，
∴∠AEC＝90°﹣∠CAE＝48°，
∵AE平分∠BAD，
∴∠DAE＝∠BAE，
设∠DAE＝x，
∵AD＝BD，
∴∠DAB＝∠B＝2x，
∴∠AEC＝∠B+∠BAE＝3x
∴3x＝48°，
∴x＝16°，
∴∠B＝2x＝32°．
四.解答题：本大题5小题，共50分
23．（8分）如图，四边形ABCD中，AB∥DC，DB平分∠ADC，∠A＝60°．
求证：△ABD是等边三角形．
【解答】证明：∵AB∥DC，∠A＝60°，
∴∠ADC＝120°，
∵DB平分∠ADC，
∴∠ADB＝＝60°＝∠A，
∴∠A＝∠ADB＝∠ABD＝60°，
∴△ADB是等边三角形．
24．（10分）如图，在△ABC中，CD是AB边上的高，BE是AC边上的中线，且BD＝CE．求证：
（1）点D在BE的垂直平分线上；
（2）∠BEC＝3∠ABE．
【解答】解：（1）连接DE，
∵CD是AB边上的高，
∴∠ADC＝∠BDC＝90°，
∵BE是AC边上的中线，
∴AE＝CE，
∴DE＝CE，
∵BD＝CE，
∴BD＝DE，
∴点D在BE的垂直平分线上；
（2）∵DE＝AE，
∴∠A＝∠ADE，
∵∠ADE＝∠DBE+∠DEB，
∵BD＝DE，
∴∠DBE＝∠DEB，
∴∠A＝∠ADE＝2∠ABE，
∵∠BEC＝∠A+∠ABE，
∴∠BEC＝3∠ABE．
25．（10分）如图，△ABC和△ADE关于直线MN对称，BC与DE的交点F在直线MN上．
（1）图中点C的对应点是点 E ，∠B的对应角是 ∠D ；
（2）若DE＝5，BF＝2，则CF的长为 3 ；
（3）若∠BAC＝108°，∠BAE＝30°，求∠EAF的度数．
【解答】解：（1）∵△ABC与△ADE关于直线MN对称，
∴图中点C的对应点是点E，∠B的对应角是∠D；
故答案为：E，∠D．
（2）∵△ABC与△ADE关于直线MN对称，
∴△ABC≌△ADE，
∴BC＝DE＝5，
∴CF＝BC﹣BF＝3．
故答案为：3．
（3）∵∠BAC＝108°，∠BAE＝30°，
∴∠CAE＝108°﹣30°＝78°，
再根据对称性，
∴∠EAF＝∠CAF，
∴∠EAF＝＝39°．
26．（10分）如图，△ABC中，D为BC上一点，∠ADC＝60°，AE⊥BC于点E，CF⊥AD于点F，AE、CF相交于点G，∠CAE＝15°．
（1）求∠ACF的度数；
（2）求证：．
【解答】（1）解：∵∠ABC＝45°，∠ADC＝60°，
∴∠BAD＝∠ADC﹣∠ABC＝60°﹣45°＝15°，
∵AE⊥BC，
∴∠AEB＝90°，
∴△ABE是等腰直角三角形，
∴∠BAE＝45°，
∴∠DAE＝∠BAE﹣∠BAD＝45°﹣15°＝30°，
∴∠CAF＝∠DAE+∠CAE＝30°+15°＝45°，
∵CF⊥AD，
∴∠AFC＝90°，
∴∠ACF＝90°﹣∠CAF＝45°；
（2）证明：由（1）可知，∠DAC＝45°，∠AFG＝∠CFD＝90°，∠ACF＝∠CAF＝45°，
∴AF＝CF，
∵AE⊥CB，
∴∠CEG＝∠AFG＝90°，
∵∠CGE＝∠AGF，
∴∠FAG＝∠FCD，
在△AFG和△CFD中，
，
∴△AFG≌△CFD（ASA），
∴GF＝DF，
由（1）可知，∠FAG＝30°，
∵∠AFG＝90°，
∴FG＝AG，
∴DF＝AG．
27．（12分）小明发现这样一个规律：两个顶角相等的等腰三角形，如果具有公共的顶角的顶点，并把它们的底角顶点连接起来，则形成一组全等三角形，小明把具有这个规律的图形称为“手拉手”图形．
（1）问题发现：在图1的“手拉手”图形中，若△ABC和△ADE均是顶角为40°的等腰三角形，BC，DE分别是底边，求证：BD＝CE；
（2）拓展探究：如图2，若△ABC和△CDE均是等边三角形，点A，D，E在同一条直线上，连接BE，则∠AEB＝ 60 °，线段BE与AD之间的数量关系是 BE＝AD ；
（3）解决问题：如图3，若△ABC和△DCE均是等腰直角三角形，∠ACB＝∠DCE＝90°，点A，D，E在同一条直线上，CM为△DCE中DE边上的高，连接BE，请求出∠AEB的度数，写出线段CM，AE，BE之间的数量关系，并说明理由．
【解答】（1）证明；∵△ABC和△ADE均是顶角为40°的等腰三角形，
∴AB＝AC，AD＝AE，∠BAC＝∠DAE，
∴∠BAC﹣∠CAD＝∠DAE﹣∠CAD，
∴∠BAD＝∠CAE，
∴△BAD≌△CAE（SAS），
∴BD＝CE；
（2）解：∵△ABC和△CDE均是等边三角形，
∴CA＝CB，CD＝CE，∠ACB＝∠DCE＝∠CDE＝∠CED＝60°，
∴∠ACB﹣∠BCD＝∠DCE﹣∠BCD，
∴∠ACD＝∠BCE，
∴△ACD≌△BCE（SAS），
∴AD＝BE，∠ADC＝∠BEC，
∵∠CDE＝60°，
∴∠BEC＝∠ADC＝180°﹣∠CDE＝120°，
∵∠CED＝60°，
∴∠AEB＝∠BEC﹣∠CED＝60°，
故答案为：60，BE＝AD；
（3）解：∠AEB＝90°，AE＝BE+2CM，理由：
同（1）（2）的方法得，△ACD≌△BCE（SAS），
∴AD＝BE，∠ADC＝∠BEC，
∵△CDE是等腰直角三角形，
∴∠CDE＝∠CED＝45°，
∴∠ADC＝180°﹣∠CDE＝135°，
∴∠BEC＝∠ADC＝135°，
∴∠AEB＝∠BEC﹣∠CED＝135°﹣45°＝90°，
∵CD＝CE，CM⊥DE，
∴DM＝ME，
∵∠DCE＝90°，
∴DM＝ME＝CM．
∴AE＝AD+DE＝BE+2CM．