辽宁省丹东市第十九中学2023-2024学年九年级上学期10月月考数学试题

这是一份辽宁省丹东市第十九中学2023-2024学年九年级上学期10月月考数学试题，文件包含部编七年级上册语文第五单元教材知识点考点梳理pptx、部编七年级上册语文第五单元教材知识点考点梳理教案docx、部编七年级上册语文第五单元教材知识点考点梳理验收卷原卷版docx、部编七年级上册语文第五单元教材知识点考点梳理验收卷解析版docx等4份课件配套教学资源，其中PPT共31页， 欢迎下载使用。
A．3﹣5x2＝xB．+x2﹣1＝0
C．ax2+bx+c＝0D．4x﹣1＝0
2．（2分）已知a：b：c＝2：3：4，则的值（ ）
A．B．1C．﹣1D．或﹣1
3．（2分）如图，在△ABC中，DE∥BC，＝，则EC＝（ ）
A．B．C．D．
4．（2分）已知一元二次方程ax2+bx+c＝0，根据下列表格中的对应值：
可判断方程的一个解x的范围是（ ）
A．3.08＜x＜3.09B．3.09＜x＜3.10
C．3.10＜x＜3.11D．3.11＜x＜3.12
5．（2分）如图，四边形ABCD是平行四边形，下列结论中错误的是（ ）
A．当∠ABC＝90°，平行四边形ABCD是矩形
B．当AC＝BD，平行四边形ABCD是矩形
C．当AB＝BC，平行四边形ABCD是菱形
D．当AC⊥BD，平行四边形ABCD是正方形
6．（2分）大自然是美的设计师，即使是一片小小的树叶，也蕴含着“黄金分割”，P为AB的黄金分割点（AP＞PB），则下列结论中正确的是（ ）
A．AB2＝AP2+BP2B．BP2＝AP•BA
C．D．
7．（2分）某建筑工程队在工地一边靠墙处，用81米长的铁栅栏围成三个相连的长方形仓库，仓库总面积为440平方米．为了方便取物，在平行于墙的一边留下一个1米宽的缺口作小门．若设AB＝x米，则可列方程（ ）
A．x（81﹣4x）＝440B．x（78﹣2x）＝440
C．x（84﹣2x）＝440D．x（84﹣4x）＝440
8．（2分）如图，矩形ABCD的对角线AC、BD相交于点O，∠AOB＝120°，DE∥AC，若AD＝2（ ）
A．4B．8C．10D．12
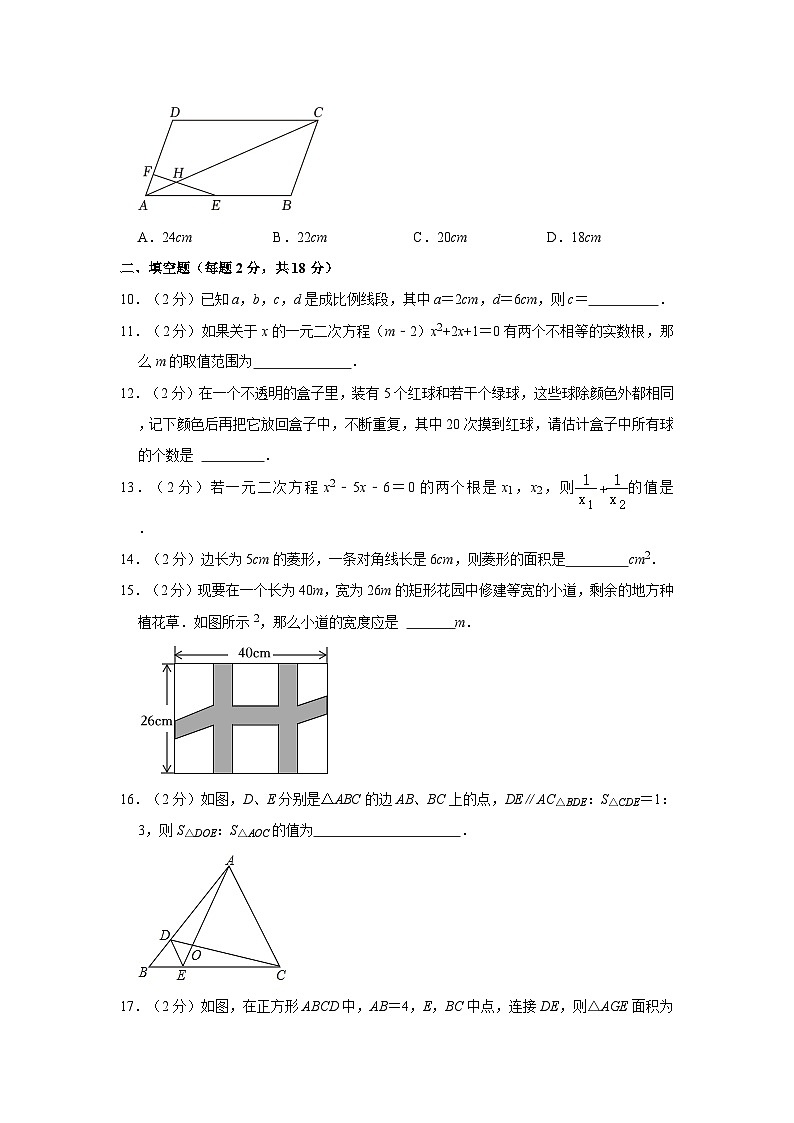
9．（2分）如图，在平行四边形ABCD中E为AB的中点，F为AD上一点，FH＝3cm，EH＝6cm，则HC的长为（ ）
A．24cmB．22cmC．20cmD．18cm
二、填空题（每题2分，共18分）
10．（2分）已知a，b，c，d是成比例线段，其中a＝2cm，d＝6cm，则c＝ ．
11．（2分）如果关于x的一元二次方程（m﹣2）x2+2x+1＝0有两个不相等的实数根，那么m的取值范围为 ．
12．（2分）在一个不透明的盒子里，装有5个红球和若干个绿球，这些球除颜色外都相同，记下颜色后再把它放回盒子中，不断重复，其中20次摸到红球，请估计盒子中所有球的个数是 ．
13．（2分）若一元二次方程x2﹣5x﹣6＝0的两个根是x1，x2，则的值是 ．
14．（2分）边长为5cm的菱形，一条对角线长是6cm，则菱形的面积是 cm2．
15．（2分）现要在一个长为40m，宽为26m的矩形花园中修建等宽的小道，剩余的地方种植花草．如图所示2，那么小道的宽度应是 m．
16．（2分）如图，D、E分别是△ABC的边AB、BC上的点，DE∥AC△BDE：S△CDE＝1：3，则S△DOE：S△AOC的值为 ．
17．（2分）如图，在正方形ABCD中，AB＝4，E，BC中点，连接DE，则△AGE面积为 ．
18．（2分）如图，在矩形纸片ABCD中，AB＝6，点E在CD上，将△BCE沿BE折叠，点G在AF上，将△ABG沿BG折叠，有下列结论：①∠EBC＝45°；②2S△BFG＝5S△FGB；③△DEF∽△ABG；④4CE＝5ED．其中正确的是 .（填写所有正确结论的序号）
三、解答题（19题8分，20题6分，21题6分，共20分）
19．（8分）解方程：
（1）x2﹣4x﹣8＝0（用公式法）．
（2）（x﹣2）2＝2x﹣4（用因式分解法）．
20．（6分）在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，﹣2），B（2，﹣1），C（4，﹣3）．
（1）画出△ABC关于x轴对称的△A1B1C1；
（2）以点O为位似中心，在网格中画出△A1B1C1的位似图形△A2B2C2，使△A2B2C2与△A1B1C1的相似比为2：1；
（3）设点P（a，b）为△ABC内一点，则依上述两次变换后点P在△A2B2C2内的对应点P2的坐标是 ．
21．（6分）某学校开展“垃圾分类，从我做起”的宣讲活动，该活动的宣讲员从甲、乙、丙、丁四名学生中随机抽选．
（1）若只抽选一名学生，乙被选中的概率为 ，
（2）若随机抽选两名学生，请用列表法或画树状图法求乙被选中的概率．
四、（每小题8分，共24分）
22．（8分）某商场将进货价为30元的台灯以40元售出，1月销售400个，2，3月这种台灯销售量持续增加，3月的销售量达到576个，设2
（1）求2，3两个月的销售量月平均增长率；
（2）从4月起，在3月销售量的基础上，商场决定降价促销．经调查发现，这种台灯的售价每降价0.5元，其销售量增加6个．这种台灯售价定为多少时
23．（8分）如图，菱形ABCD的对角线AC与BD相交于点O，DE⊥AB于点E交AC于点P
（1）判断四边形DEBF的形状，并说明理由；
（2）如果BE＝3，BF＝6，求出DP的长．
24．（8分）如图，在正方形ABCD中，点E是对角线AC上的一点，交AB于点G．
（1）求证：△BEG∽△FEB；
（2）当BF＝1，BC＝3时，求EG的长．
五、（本题满分10分）
25．（10分）已知点C为△ABC和△CDE的公共顶点，将△CDE绕点C顺时针旋转α（0°＜α＜360°），连接BD，请完成如下问题：
（1）如图1，若△ABC和△CDE均为等边三角形，线段BD与线段AE的数量关系是 ；
类比探究：
（2）如图2，若∠ABC＝∠EDC＝90°，∠ACB＝∠ECD＝60°，请写出线段BD与线段AE的数量关系，并说明理由；
（3）拓展应用：如图3，D是△ABC内一点，∠BAD＝∠CBD＝30°，AB＝4，，直接写出AD的长．
六、（本题满分10分）
26．（10分）如图，在平面直角坐标系中，直线y＝2x+4交坐标轴于点C，D，以OA和OC为邻边作矩形OABC，点E是直线AB上一动点．
（1）写出点B的坐标；
（2）连接DE，若DE平分∠ADC，求出点E的坐标；
（3）若点F是纵轴（y轴）左侧任意一点，是否存在以C，D，E，若存在，直接写出点F坐标，请说明理由．
2023-2024学年辽宁省丹东十九中九年级（上）月考数学试卷（10月份）
参考答案与试题解析
一.选择题（下列各题的备选答案中，只有一个是正确的.每小题2分，共18分）
1．（2分）下列各式是一元二次方程的是（ ）
A．3﹣5x2＝xB．+x2﹣1＝0
C．ax2+bx+c＝0D．4x﹣1＝0
【答案】A
【分析】本题根据一元二次方程的定义解答．一元二次方程必须满足四个条件：（1）未知数的最高次数是2；（2）二次项系数不为0；（3）是整式方程；（4）含有一个未知数．由这四个条件对四个选项进行验证，满足这四个条件者为正确答案．
【解答】解：A、符合一元二次方程的定义；
B、不是整式方程；
C、方程二次项系数可能为0；
D、方程未知数为1次；
故选：A．
2．（2分）已知a：b：c＝2：3：4，则的值（ ）
A．B．1C．﹣1D．或﹣1
【答案】B
【分析】根据比例性质，可用a表示b，用a表示c，根据分式的性质，可得答案．
【解答】解：由a：b：c＝2：3：3，得
b＝，c＝4a．
＝＝＝1，
故选：B．
3．（2分）如图，在△ABC中，DE∥BC，＝，则EC＝（ ）
A．B．C．D．
【答案】C
【分析】利用平行线分线段成比例定理解答即可．
【解答】解：∵DE∥BC，
∴＝，
∴，
∴，
∴EC＝．
故选：C．
4．（2分）已知一元二次方程ax2+bx+c＝0，根据下列表格中的对应值：
可判断方程的一个解x的范围是（ ）
A．3.08＜x＜3.09B．3.09＜x＜3.10
C．3.10＜x＜3.11D．3.11＜x＜3.12
【答案】D
【分析】观察表格可知，随x的值逐渐增大，ax2+bx+c的值在3.11～3.12之间由负到正，故可判断ax2+bx+c＝0时，对应的x的值在3.11～3.12之间．
【解答】解：根据表格可知，ax2+bx+c＝0时，对应的x的值在2.11～3.12之间．
故选：D．
5．（2分）如图，四边形ABCD是平行四边形，下列结论中错误的是（ ）
A．当∠ABC＝90°，平行四边形ABCD是矩形
B．当AC＝BD，平行四边形ABCD是矩形
C．当AB＝BC，平行四边形ABCD是菱形
D．当AC⊥BD，平行四边形ABCD是正方形
【答案】D
【分析】根据有一个角是直角的平行四边形是矩形可以判断A；根据对角线相等的平行四边形是矩形可以判断B；根据有一组邻边相等的平行四边形是菱形可以判断C；根据对角线互相垂直的平行四边形是菱形可以判断D．
【解答】解：∵四边形ABCD是平行四边形，
∴当∠ABC＝90°，平行四边形ABCD是矩形，不符合题意；
当AC＝BD，平行四边形ABCD是矩形，不符合题意；
当AB＝BC，平行四边形ABCD是菱形，不符合题意；
当AC⊥BD，平行四边形ABCD是菱形，故选项D错误；
故选：D．
6．（2分）大自然是美的设计师，即使是一片小小的树叶，也蕴含着“黄金分割”，P为AB的黄金分割点（AP＞PB），则下列结论中正确的是（ ）
A．AB2＝AP2+BP2B．BP2＝AP•BA
C．D．
【答案】D
【分析】由黄金分割的定义得AP2＝BP•BA，＝＝，即可求解．
【解答】解：∵P为AB的黄金分割点（AP＞PB），
∴AP2＝BP•BA，＝＝，故选项A、B，选项D符合题意，
故选：D．
7．（2分）某建筑工程队在工地一边靠墙处，用81米长的铁栅栏围成三个相连的长方形仓库，仓库总面积为440平方米．为了方便取物，在平行于墙的一边留下一个1米宽的缺口作小门．若设AB＝x米，则可列方程（ ）
A．x（81﹣4x）＝440B．x（78﹣2x）＝440
C．x（84﹣2x）＝440D．x（84﹣4x）＝440
【答案】D
【分析】设仓库的宽为x米（AB＝x米），由铁栅栏的长度结合图形，可求出仓库的长为（84﹣4x）米，再根据矩形的面积公式即可列出关于x的一元二次方程，此题得解．
【解答】解：设仓库的宽为x米（AB＝x米），则仓库的长为（84﹣4x）米，
根据题意得：x（84﹣4x）＝440．
故选：D．
8．（2分）如图，矩形ABCD的对角线AC、BD相交于点O，∠AOB＝120°，DE∥AC，若AD＝2（ ）
A．4B．8C．10D．12
【答案】B
【分析】首先由CE∥BD，DE∥AC，可证得四边形CODE是平行四边形，又由四边形ABCD是矩形，根据矩形的性质，易得OC＝OD＝2，即可判定四边形CODE是菱形，继而求得答案．
【解答】解：∵四边形ABCD是矩形，
∴BD＝AC，DO＝BO，
∴OD＝OA，
∵∠AOB＝120°，
∴∠DOA＝60°，
∴△AOD是等边三角形，
∴DO＝AO＝AD＝OC＝2，
∵CE∥BD，DE∥AC，
∴四边形CODE是平行四边形，
∴四边形CODE是菱形，
∴四边形CODE的周长为：4OC＝8×2＝8，
故选：B．
9．（2分）如图，在平行四边形ABCD中E为AB的中点，F为AD上一点，FH＝3cm，EH＝6cm，则HC的长为（ ）
A．24cmB．22cmC．20cmD．18cm
【答案】C
【分析】延长FE交CB的延长线于点G．证明△AFE≌△BGE，得出EG＝EF，求出EG＝9cm，根据平行线分线段成比例定理，得出＝，代入求出结果即可．
【解答】解：延长FE交CB的延长线于点G，如图所示：
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠EAF＝∠EBG，∠AFE＝∠BGE，
∵E为AB的中点，
∴AE＝BE，
∴△AFE≌△BGE，
∴EG＝EF，
∵EF＝EH+FH＝3+6＝6（cm），
∴EG＝9cm，
∴GH＝GE+EH＝9+5＝15（cm），
∵AD∥BC，
∴＝，
即＝，
解得：CH＝20cm，故C正确．
故选：C．
二、填空题（每题2分，共18分）
10．（2分）已知a，b，c，d是成比例线段，其中a＝2cm，d＝6cm，则c＝ 4cm ．
【答案】见试题解答内容
【分析】根据比例线段的定义得到a：b＝c：d，然后把a＝2cm，b＝3cm，d＝6cm代入进行计算即可．
【解答】解：∵a，b，c，d是成比例线段，
∴a：b＝c：d，
而a＝2cm，b＝3cm，
∴c＝＝＝5（cm）．
故答案为4cm．
11．（2分）如果关于x的一元二次方程（m﹣2）x2+2x+1＝0有两个不相等的实数根，那么m的取值范围为 m＜3且m≠2 ．
【答案】见试题解答内容
【分析】根据根的判别式即可求出答案．
【解答】解：由题意可知：Δ＝4﹣4（m﹣6）＞0，
∴m＜3，
由于m﹣3≠0，
∴m≠2，
故答案为：m＜7且m≠2
12．（2分）在一个不透明的盒子里，装有5个红球和若干个绿球，这些球除颜色外都相同，记下颜色后再把它放回盒子中，不断重复，其中20次摸到红球，请估计盒子中所有球的个数是 20 ．
【答案】见试题解答内容
【分析】在同样条件下，大量反复试验时，随机事件发生的频率逐渐稳定在概率附近，可以从比例关系入手，设未知数列出方程求解．
【解答】解：∵共试验80次，其中有20次摸到红球，
∴红球所占的比例为＝，
设盒子中共有球x个，则＝，
解得：x＝20．
故答案为：20．
13．（2分）若一元二次方程x2﹣5x﹣6＝0的两个根是x1，x2，则的值是 ﹣ ．
【答案】﹣．
【分析】由根与系数的关系得出两根之和，两根之积，然后把要求的式子变形，代入求值即可．
【解答】解：∵一元二次方程x2﹣5x﹣8＝0的两个根是x1，x4，
∴x1+x2＝8，x1x2＝﹣8，
∴
＝
＝
＝﹣．
故答案为：﹣．
14．（2分）边长为5cm的菱形，一条对角线长是6cm，则菱形的面积是 24 cm2．
【答案】见试题解答内容
【分析】根据菱形对角线垂直且互相平分，即可得出菱形的另一条对角线的长，再利用菱形的面积公式求出即可．
【解答】解：如图所示：设BD＝6cm，AD＝5cm，
∴BO＝DO＝7cm，
∴AO＝CO＝＝4（cm），
∴AC＝8cm，
∴菱形的面积是：×7×8＝24（cm2）．
故答案为：24．
15．（2分）现要在一个长为40m，宽为26m的矩形花园中修建等宽的小道，剩余的地方种植花草．如图所示2，那么小道的宽度应是 2 m．
【答案】见试题解答内容
【分析】设小道进出口的宽度为x米，然后利用其种植花草的面积为864m2列出方程求解即可．
【解答】解：设小道进出口的宽度为x米，依题意得（40﹣2x）（26﹣x）＝864，
整理，得x2﹣46x+88＝2．
解得，x1＝2，x4＝44．
∵44＞40（不合题意，舍去），
∴x＝2．
答：小道进出口的宽度应为2米．
故答案为：2．
16．（2分）如图，D、E分别是△ABC的边AB、BC上的点，DE∥AC△BDE：S△CDE＝1：3，则S△DOE：S△AOC的值为 ．
【答案】．
【分析】证明BE：EC＝1：3，得出BE：BC＝1：4；证明△BDE∽△BAC，△DOE∽△AOC，得到＝，由相似三角形的性质即可解决问题．
【解答】解：∵S△BDE：S△CDE＝1：3，
∴BE：EC＝5：3；
∴BE：BC＝1：5；
∵DE∥AC，
∴△BDE∽△BAC，△DOE∽△AOC，
∴＝，
∴S△DOE：S△AOC＝（）5＝；
故答案为：．
17．（2分）如图，在正方形ABCD中，AB＝4，E，BC中点，连接DE，则△AGE面积为 ．
【答案】．
【分析】根据正方形的性质和全等三角形的判定和性质得出∠AEG+∠EAG＝90°，进而利用相似三角形的判定和性质解答即可．
【解答】解：∵四边形ABCD是正方形，
∴AD＝AB＝BC，∠B＝∠EAD＝90°，
∵E，F分别为边AB，
∴AE＝ABBC，
∴AE＝BF＝2，
∴AF＝，
在△ABF与△DAE中，
，
∴△ABF≌△DAE（SAS），
∴∠ADE＝∠BAF，
∵∠ADE+∠AED＝90°，
∴∠BAF+∠AED＝90°，
∴∠AGE＝90°，
∴△AEG∽△AFB，
∴，
∴，
∴△AGE面积＝，
故答案为：．
18．（2分）如图，在矩形纸片ABCD中，AB＝6，点E在CD上，将△BCE沿BE折叠，点G在AF上，将△ABG沿BG折叠，有下列结论：①∠EBC＝45°；②2S△BFG＝5S△FGB；③△DEF∽△ABG；④4CE＝5ED．其中正确的是 ①②④ .（填写所有正确结论的序号）
【答案】①②④．
【分析】①根据折叠、矩形的性质进行推理即可；②根据等高三角形的面积比等于底边的比计算分析即可；③由矩形的性质、勾股定理及相似三角形的判定定理计算分析即可；④由矩形的性质可得CD的长，根据CE＝CD﹣ED求得CE的值，则可求得答案．
【解答】解：①由折叠的性质可知：∠CBE＝∠FBE，∠ABG＝∠FBG，
∵四边形ABCD是矩形，
∴∠ABC＝90°，
∴∠EBG＝∠GBH+∠EBF＝∠CBF+∠ABC＝45°．
故①正确；
②由折叠的性质可知：BF＝BC＝10，BH＝AB＝6，
∴HF＝BF﹣BH＝4，
∴＝＝，
∴2S△BFG＝8S△FGH；
故②正确；
③∵四边形ABCD是矩形，
∴∠A＝∠D＝90°，
在Rt△ABF中，AF＝，
设GF＝x，即HG＝AG＝8﹣x，
在Rt△HGF中，HG2+HF2＝GF3，
即（8﹣x）2+42＝x2，解得x＝7，
∴AG＝3，
∴FD＝2；
同理可得ED＝，
∴＝2，＝，
∴≠，
∴△ABG与△DEF不相似，
故③错误；
④∵CD＝AB＝6，ED＝，
∴CE＝CD﹣ED＝，
∴，
∴4CE＝5ED．
故④正确．
故答案为：①②④．
三、解答题（19题8分，20题6分，21题6分，共20分）
19．（8分）解方程：
（1）x2﹣4x﹣8＝0（用公式法）．
（2）（x﹣2）2＝2x﹣4（用因式分解法）．
【答案】（1）x1＝2+2，x2＝2﹣2；
（2）x1＝2，x2＝4．
【分析】（1）先计算出根的判别式的值，然后利用求根公式得到方程的解；
（2）先移项，再利用因式分解法把方程转化为x﹣2＝0或x﹣4＝0，然后解两个一次方程即可．
【解答】解：（1）x2﹣4x﹣6＝0，
∵a＝1，b＝﹣7，
∴Δ＝（﹣4）2﹣8×1×（﹣8）＝48＞3，
∴x＝＝6，
所以x3＝2+2，x2＝2﹣3；
（2）（x﹣2）5＝2x﹣4，
（x﹣3）2﹣2（x﹣4）＝0，
（x﹣2）（x﹣2﹣2）＝0，
x﹣3＝0或x﹣4＝6，
所以x1＝2，x3＝4．
20．（6分）在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，﹣2），B（2，﹣1），C（4，﹣3）．
（1）画出△ABC关于x轴对称的△A1B1C1；
（2）以点O为位似中心，在网格中画出△A1B1C1的位似图形△A2B2C2，使△A2B2C2与△A1B1C1的相似比为2：1；
（3）设点P（a，b）为△ABC内一点，则依上述两次变换后点P在△A2B2C2内的对应点P2的坐标是 （2a，﹣2b） ．
【答案】见试题解答内容
【分析】（1）利用关于x轴对称的点的坐标特征写出A1、B1、C1的坐标，然后描点即可；
（2）利用关于原点为位似中心的对应点的坐标之间的关系，把点A1、B1、C1的横纵坐标都乘以2得到A2、B2、C2的坐标，然后描点即可；
（3）利用（2）中的坐标变换规律求解．
【解答】解：（1）如图，△A1B1C6为所作；
（2）如图，△A2B2C7为所作；
（3）点P的对应点P2的坐标是（2a，﹣3b）．
故答案为（2a，﹣2b）．
21．（6分）某学校开展“垃圾分类，从我做起”的宣讲活动，该活动的宣讲员从甲、乙、丙、丁四名学生中随机抽选．
（1）若只抽选一名学生，乙被选中的概率为 ，
（2）若随机抽选两名学生，请用列表法或画树状图法求乙被选中的概率．
【答案】见试题解答内容
【分析】（1）直接利用概率公式计算；
（2）画树状图展示12种等可能的结果数，再找出乙被选中的结果数，然后根据概率公式计算．
【解答】解：（1）若只抽选一名学生，乙被选中的概率＝；
故答案为；
（2）画树状图为：
共有12种等可能的结果，其中乙被选中的结果数为6，
所以乙被选中的概率＝＝．
四、（每小题8分，共24分）
22．（8分）某商场将进货价为30元的台灯以40元售出，1月销售400个，2，3月这种台灯销售量持续增加，3月的销售量达到576个，设2
（1）求2，3两个月的销售量月平均增长率；
（2）从4月起，在3月销售量的基础上，商场决定降价促销．经调查发现，这种台灯的售价每降价0.5元，其销售量增加6个．这种台灯售价定为多少时
【答案】（1）20%；
（2）38元．
【分析】（1）设2，3两个月这种台灯销售量的月均增长率为x，利用三月份的销售量＝一月份的销售量×（1+月均增长率）2，即可得出关于x的一元二次方程，解之取其正值即可得出结论；
（2）解法一：设每台降价y元，则每台的销售利润为（40﹣y﹣30）元，四月份可售出（576+12y）台，利用总利润＝每台的销售利润×四月份的销售量，即可得出关于y的一元二次方程，解之取其正值即可得出结论；
解法二：设每台售价定为y元，则每台的销售利润为（y﹣30）元，四月份可售出[576+12（40﹣y）]台，利用总利润＝每台的销售利润×四月份的销售量，即可得出关于y的一元二次方程，解之取其正值即可得出结论．
【解答】解：（1）设2，3两个月的销售量月平均增长率为x，
依题意，得：400（3+x）2＝576，
解得：x1＝7.2＝20%，x2＝﹣7.2（不符合题意，舍去）．
答：2，5两个月的销售量月平均增长率为20%．
（2）解法一：设这种台灯每个降价y元时，商场四月份销售这种台灯获利4800元，
依题意，得：（40﹣y﹣30）（576+12y）＝4800，
整理，得：y2+38y﹣80＝0，
解得y2＝2，y2＝﹣40（不符合题意，舍去），
当y＝6时，40﹣y＝38．
答：该种台灯售价定为38元时，商场四月份销售这种台灯获利4800元．
解法二：设这种台灯售价定为y元时，商场四月份销售这种台灯获利4800元，
依题意，得：（y﹣30）[576+12（40﹣y）]＝4800，
整理，得y2﹣118y+3040＝0，
解得y7＝38，y2＝80（不符合题意，舍去）．
答：该种台灯售价定为38元时，商场四月份销售这种台灯获利4800元．
23．（8分）如图，菱形ABCD的对角线AC与BD相交于点O，DE⊥AB于点E交AC于点P
（1）判断四边形DEBF的形状，并说明理由；
（2）如果BE＝3，BF＝6，求出DP的长．
【答案】（1）四边形DEBF是矩形，理由见解析；
（2）．
【分析】（1）根据菱形的性质和矩形的判定解答即可；
（2）根据菱形的性质和矩形的性质得出DE＝BF，进而利用勾股定理解答即可．
【解答】（1）解：四边形DEBF是矩形，理由如下：
∵DE⊥AB，BF⊥CD，
∴∠DEB＝∠BFD＝90°，
∵四边形ABCD是菱形，
∴AB∥CD，
∴∠DEB+∠EDF＝180°，
∴∠EDF＝∠DEB＝∠BFD＝90°，
∴四边形DEBF是矩形；
（2）解：连接PB，
∵四边形ABCD是菱形，
∴AC垂直平分BD，
∴PB＝PD，
由（1）知，四边形DEBF是矩形，
∴DE＝FB＝6，
设PD＝BP＝x，则PE＝6﹣x，
在Rt△PEB中，由勾股定理得：（3﹣x）2+34＝x2，
解得：x＝，
∴PD＝．
24．（8分）如图，在正方形ABCD中，点E是对角线AC上的一点，交AB于点G．
（1）求证：△BEG∽△FEB；
（2）当BF＝1，BC＝3时，求EG的长．
【答案】（1）证明见解答过程；
（2）．
【分析】（1）根据正方形的性质推出AD∥BC，AD＝AB，∠DAC＝∠BAC＝45°，利用SAS证明△ADE≌△ABE，根据全等三角形的性质得出∠ADE＝∠ABE，根据平行线的性质得出∠ADE＝∠F，结合∠BEG＝∠FEB，即可判定△BEG∽△FEB；
（2）结合正方形的性质、勾股定理求出AB∥CD，∠DCB＝90°，AD＝DC＝BC＝3，DF＝5，根据平行线的性质推出＝，△ADE∽△CFE，结合相似三角形的性质求出FG＝，EF＝，根据线段的和差求解即可．
【解答】（1）证明：∵四边形ABCD是正方形，
∴AD∥BC，AD＝AB，
∵AE＝AE，
∴△ADE≌△ABE（SAS），
∴∠ADE＝∠ABE，
∵AD∥BC，
∴∠ADE＝∠F，
又∠BEG＝∠FEB，
∴△BEG∽△FEB；
（2）解：∵四边形ABCD是正方形，
∴AB∥CD，∠DCB＝90°，
∴CF＝BC+BF＝3+1＝4，
∴DF＝＝4，
∵AB∥CD，
∴＝，
∴＝，
∴FG＝，
∵AD∥BC，
∴∠ADE＝∠F，∠DAE＝∠FCE，
∴△ADE∽△CFE，
∴＝，
∴＝，
∴EF＝，
∴EG＝EF﹣FG＝﹣＝．
五、（本题满分10分）
25．（10分）已知点C为△ABC和△CDE的公共顶点，将△CDE绕点C顺时针旋转α（0°＜α＜360°），连接BD，请完成如下问题：
（1）如图1，若△ABC和△CDE均为等边三角形，线段BD与线段AE的数量关系是 BD＝AE ；
类比探究：
（2）如图2，若∠ABC＝∠EDC＝90°，∠ACB＝∠ECD＝60°，请写出线段BD与线段AE的数量关系，并说明理由；
（3）拓展应用：如图3，D是△ABC内一点，∠BAD＝∠CBD＝30°，AB＝4，，直接写出AD的长．
【答案】（1）结论：BD＝AE．理由见解析部分；
（2）结论：．理由见解析部分；
（3）．
【分析】（1）结论：BD＝AE．证明△BCD≌△ACE（SAS），可得结论；
（2）结论：．延长AE交BD的延长线于点F，AC交BF于点O．证明△BCD∽△ACE，推出，可得结论；
（3）如图2，过点A作AB的垂线，过点D作AD的垂线，两垂线交于点M，连接BM，证明△BDM∽△CDA，推出，可得结论．
【解答】解：（1）结论：BD＝AE．
理由：∵△ABC和△CDE均为等边三角形，
∴CB＝CA，CD＝CE，
∴∠BCD＝∠ACE，
∴△BCD≌△ACE（SAS），
∴BD＝AE；
（2）结论：．
理由：延长AE交BD的延长线于点F，AC交BF于点O．
∵∠ABC＝∠EDC＝90°，∠ACB＝∠ECD＝60°，
∴∠BAC＝∠DEC＝30°，∠ACB﹣∠ACD＝∠ECD﹣∠ACD，
∴，∠BCD＝∠ECA，
∴△BCD∽△ACE，
∴，
∴；
（3）如图5，过点A作AB的垂线，两垂线交于点M，
∵∠BAD＝30°，
∴∠DAM＝60°，
∴∠AMD＝30°，
∴∠AMD＝∠DBC，
又∵∠ADM＝∠BDC＝90°，
∴△BDC∽△MDA，
∴，
又∵∠BDC＝∠ADM，
∴∠BDC+∠CDM＝∠ADM+∠CDM，即∠BDM＝∠CDA，
∴△BDM∽△CDA，
∴，
∵，
∴，
∴，
∴．
六、（本题满分10分）
26．（10分）如图，在平面直角坐标系中，直线y＝2x+4交坐标轴于点C，D，以OA和OC为邻边作矩形OABC，点E是直线AB上一动点．
（1）写出点B的坐标；
（2）连接DE，若DE平分∠ADC，求出点E的坐标；
（3）若点F是纵轴（y轴）左侧任意一点，是否存在以C，D，E，若存在，直接写出点F坐标，请说明理由．
【答案】（1）点B的坐标为（﹣3，4）；
（2）E的坐标为（﹣3，）；
（3）存在，点F的坐标为（﹣1，）或（﹣5，）．
【分析】（1）如图，根据直线y＝2x+4交坐标轴于点C，D可得C（0，4），D（﹣2，0），由AD：OD＝1：2可得AD＝1，则A（﹣3，0），根据矩形OABC即可得点B的坐标；
（2）延长CB，DE，交于点H，根据矩形的性质以及角平分线的性质可得∠H＝∠CDH，则CH＝CD，在Rt△OCD中，由勾股定理可得CD＝＝2，则H（﹣2，4），求出直线DH的解析式，即可求出点E的坐标；
（3）分CD为矩形的边和CD为矩形的对角线两种情况，分别求解即可．
【解答】解：（1）如图，
∵直线y＝2x+4交坐标轴于点C，D，
∴C（4，4），0），
∵AD：OD＝6：2，
∴AD＝1，
∴OA＝AD+OD＝8，
∴A（﹣3，0），
∵四边形OABC是矩形，
∴AB⊥OA，AB＝OC＝6，
∴点B的坐标为（﹣3，4）；
（2）延长CB，DE，
矩形OABC中，OA∥BC，
∴∠H＝∠ADH．
∵DE平分/ADC，
∴∠ADH＝∠CDH，
∴∠H＝∠CDH，
∴CH＝CD，
在Rt△OCD中，由勾股定理
CD＝＝2，
∴CH＝2．
∴H（﹣5，4），
设直线DH的解析式为y＝kx+b，
将D、H的坐标代入，得，
解得：，
∴直线DH的解析式为y＝﹣x﹣，
∵E在AB上，
∴E的横坐标为﹣3，
将x＝﹣6代入直线DH的解析式中，得：
y＝﹣×（﹣3）﹣，
∴E的坐标为（﹣5，）；
（3）①CD为矩形的边时，如图，
∵四边形CDEF是矩形，
∴∠CDE＝90°，
∴∠ADE+∠ODC＝90°，
∵四边形OABC是矩形，
∴∠DAE＝∠COD＝90°，
∴∠ADE+∠AED＝90°，
∴∠AED＝∠ODC，
∴△AED∽△ODC，
∴，
∴，
∴AE＝，
∴E（﹣5，），
∵C（2，4），0），
∴F（﹣7，）；
作F′H⊥x轴于H，
∴∠DHF′＝∠COD＝90°，F′H∥AB，
∵四边形CDE′F′是矩形，
∴CE′＝DF′，CE′∥DF′，
∴∠CE′B＝∠BEF′，
∵F′H∥AB，
∴∠BEF′＝∠DF′H，
∴∠CE′B＝∠DF′H，
∵∠CBE′＝∠DHF′＝90°，
∴△CBE′≌△DHF′（AAS），
∴DH＝BC＝OA＝8，
∴OH＝5，
∵F′H∥AB，
∴△AED∽△HF′D，
∴，
∴，
∴F′H＝，
∴F′（﹣5，）；
②CD为矩形的对角线时，如图，
同理可得：△BCE∽△AED，
∴，
∴，
∴AE＝1或8，
∴E的坐标为（﹣3，1）或（﹣8，
∵C（0，4），8），
设F（x，y），
∴﹣3+x＝﹣2+2，解得x＝1，
y+1＝8+4或y+3＝5+4，解得y＝3或2，
∴点F坐标为（1，1）或（7．
∵点F是纵轴（y轴）左侧任意一点，
∴点F坐标为（1，1）或（8，舍去．
综上，存在，）或（﹣6，）．x
…
3.09
3.10
3.11
3.12
…
ax2+bx+c
…
﹣0.17
﹣0.08
﹣0.01
0.11
…
x
…
3.09
3.10
3.11
3.12
…
ax2+bx+c
…
﹣0.17
﹣0.08
﹣0.01
0.11
…