

2023-2024学年广西贵港市港北六中九年级(上)月考数学试卷(9月份)(含解析)
展开1.已知=(a≠0,b≠0),下列变形错误的是( )
A.=B.2a=3bC.=D.3a=2b
2.下列关系式中表示y是x的反比例函数的是( )
A.B.y=2x+1C.D.
3.已知反比例函数的图象在第二、四象限,则m的取值范围是( )
A.m≥6B.m>6C.m≤6D.m<6
4.已知关于x的方程是一元二次方程,则m的值为( )
A.m=2B.m=4C.m=±2D.m=﹣2
5.将抛物线y=﹣2(x+1)2+3向右平移3个单位,再向下平移2个单位,所得抛物线解析式为( )
A.y=﹣2(x+4)2+1B.y=﹣2(x﹣2)2+1
C.y=﹣2(x+4)2+5D.y=﹣2(x﹣2)2+5
6.若关于x的一元二次方程kx2+2x+1=0有实数根,则k的取值范围是( )
A.k>0B.k≤0C.k≠1且k≠0D.k≤1且k≠0
7.如图,直线a∥b∥c,直线AC和DF被直线a,b,c所截,如果截得线段AB=3,BC=
6,EF=5,那么线段DE的长为( )
A.10B.C.D.
8.如图,∠DAB=∠CAE,请你再添加一个条件,使得△ADE∽△ABC.则下列选项不成立的是( )
A.∠D=∠BB.∠E=∠CC.D.
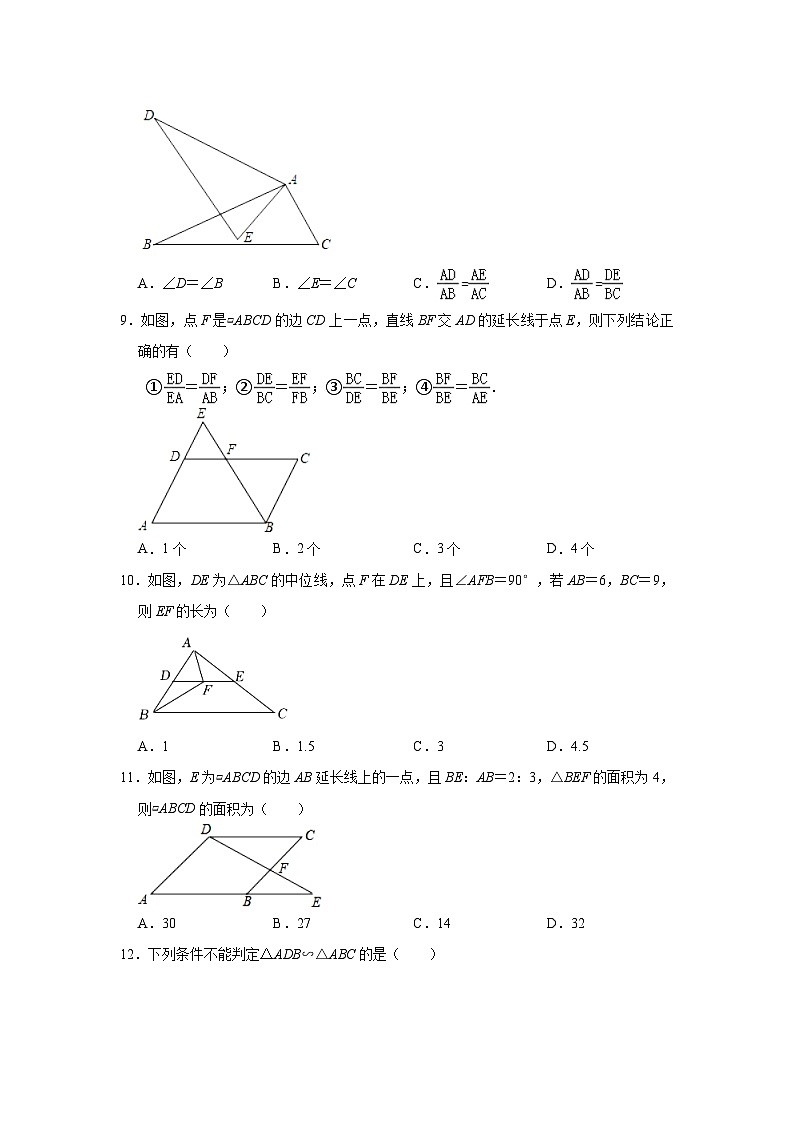
9.如图,点F是▱ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论正确的有( )
①=;②=;③=;④=.
A.1个B.2个C.3个D.4个
10.如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=9,则EF的长为( )
A.1B.1.5C.3D.4.5
11.如图,E为▱ABCD的边AB延长线上的一点,且BE:AB=2:3,△BEF的面积为4,则▱ABCD的面积为( )
A.30B.27C.14D.32
12.下列条件不能判定△ADB∽△ABC的是( )
A.∠ABD=∠ACBB.∠ADB=∠ABCC.AB2=AD•ACD.=
二.填空题(每题2分,共12分)
13.若,则= .
14.设a为一元二次方程2x2+3x﹣2022=0的一个实数根,则2﹣9a﹣6a2= .
15.若双曲线的图象经过第二、四象限,则k的取值范围是 .
16.已知点C是线段AB上的黄金分割点,且AC>BC,如果AB=2cm,那么线段BC的长度为 cm.
17.如图,在△ABC中,D为AB边上的一点,要使△ABC∽△AED成立,还需要添加一个条件为 .
18.如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为 .
三.解答题
19.解方程:
(1)x2﹣2x=2x+1
(2)2(x﹣3)=3x(x﹣3)
20.如图,在矩形ABCD中,M是BC上的一点,连接AM,DE⊥AM于点E.
(1)求证:△ADE∽△MAB;
(2)若,AD=8,BM=3,求EM的长.
21.如图,一次函数y=kx+b(k≠0)与反比例函数(m≠0,x>0)的图象交于A(1,6),B(3,n)两点,AE⊥x轴于点E,BC⊥x轴于点C.
(1)求反比例函数和一次函数的表达式;
(2)根据图象直接写出kx+b>(x>0)时的x的取值范围;
(3)求△AOB的面积.
22.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
23.2022年冬奥会在北京顺利召开,冬奥会吉祥物冰墩墩公仔爆红.据统计冰墩墩公仔在某电商平台1月份的销售量是5万件,3月份的销售量是7.2万件.
(1)若该平台1月份到3月份的月平均增长率都相同,求月平均增长率是多少?
(2)市场调查发现,某一间店铺冰墩墩公仔的进价为每件60元,若售价为每件100元,每天能销售20件,售价每降价1元,每天可多售出2件,为了推广宣传,商家决定降价促销,同时尽量减少库存,若使销售该公仔每天获利1200元,则售价应降低多少元?
24.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他站在距离树12m的地方,调整三角板DEF的位置,设法使斜边DF保持水平,并且直角边DE与树顶点B在同一直线上.已知纸板的两条直角边DE=30cm,EF=20cm,测得斜边DF离地面的高度为1.5m,求树的高度.
25.如图,矩形ABCD为台球桌面,AD=260cm,AB=130cm,球目前在E点位置,AE=60cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
26.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(1)求证:AC2=AB•AD;
(2)求证:CE∥AD;
(3)若AD=8,AB=12.求EF的长.
参考答案
一.选择题(每小题3分,共36分)
1.已知=(a≠0,b≠0),下列变形错误的是( )
A.=B.2a=3bC.=D.3a=2b
【分析】根据两内项之积等于两外项之积对各选项分析判断即可得解.
解:由=得,3a=2b,
A、由等式性质可得:3a=2b,正确;
B、由等式性质可得2a=3b,错误;
C、由等式性质可得:3a=2b,正确;
D、由等式性质可得:3a=2b,正确;
故选:B.
【点评】本题考查了比例的性质,主要利用了两内项之积等于两外项之积.
2.下列关系式中表示y是x的反比例函数的是( )
A.B.y=2x+1C.D.
【分析】根据反比例函数的定义判断即可.
解:A.y=,是反比例函数,故A符合题意;
B.y=2x+1,是一次函数,故B不符合题意;
C.y=x2,是二次函数,故C不符合题意;
D.y=,是一次函数,故D不符合题意;
故选:A.
【点评】本题考查了反比例函数的定义,熟练掌握反比例函数的定义是解题的关键.
3.已知反比例函数的图象在第二、四象限,则m的取值范围是( )
A.m≥6B.m>6C.m≤6D.m<6
【分析】由于反比例函数的图象在第二、四象限,根据反比例函数的性质可推知比例系数m﹣6<0,据此即可求出m的取值范围.
解:∵反比例函数的图象在第二、四象限,
∴m﹣6<0,
∴m<6.
故选:D.
【点评】此题考查了反比例函数的性质,解题的关键是知道:对与y=,
当k>0时,函数图象位于一、三象限;
当k<0时,函数图象位于二、四象限.
4.已知关于x的方程是一元二次方程,则m的值为( )
A.m=2B.m=4C.m=±2D.m=﹣2
【分析】根据一元二次方程的定义可得m2﹣2=2且m﹣2≠0,即可求解.
解:∵方程是一元二次方程,
∴m2﹣2=2且m﹣2≠0,
解得:m=﹣2.
故选:D.
【点评】本题主要考查了一元二次方程的定义,熟练掌握含有一个未知数,且未知数的最高次数是2的整式方程是一元二次方程是解题的关键.
5.将抛物线y=﹣2(x+1)2+3向右平移3个单位,再向下平移2个单位,所得抛物线解析式为( )
A.y=﹣2(x+4)2+1B.y=﹣2(x﹣2)2+1
C.y=﹣2(x+4)2+5D.y=﹣2(x﹣2)2+5
【分析】求出原抛物线的顶点坐标,再根据向左平移横坐标,向下平移纵坐标减求出平移后的抛物线的顶点坐标,然后利用顶点式解析式写出即可.
解:∵抛物线y=﹣2(x+1)2+3的顶点坐标为(﹣1,3),
∴向右平移3个单位,再向下平移2个单位后的顶点坐标是(2,1).
∴所得抛物线解析式是y=﹣2(x﹣2)2+1.
故选:B.
【点评】本题考查的是二次函数的图象与几何变换,熟知函数图象平移的法则是解答此题的关键.
6.若关于x的一元二次方程kx2+2x+1=0有实数根,则k的取值范围是( )
A.k>0B.k≤0C.k≠1且k≠0D.k≤1且k≠0
【分析】根据根的判别式结合一元二次方程的定义即可求解.
解:由题意:Δ=22﹣4k≥0且k≠0,
∴k≤1且k≠0,
故选:D.
【点评】本题考查了一元二次方程的定义与根的判别式,解题关键是掌握当Δ≥0时,方程才有实数根.
7.如图,直线a∥b∥c,直线AC和DF被直线a,b,c所截,如果截得线段AB=3,BC=
6,EF=5,那么线段DE的长为( )
A.10B.C.D.
【分析】根据平行线分线段成比例定理得出比例式,代入求出即可.
解:∵直线a∥b∥c,
∴=,
∵AB=3,BC=6,EF=5,
∴=,
∴DE=.
故选:C.
【点评】本题考查了平行线分线段成比例定理,能根据平行线分线段成比例定理得出正确的比例式是解此题的关键.
8.如图,∠DAB=∠CAE,请你再添加一个条件,使得△ADE∽△ABC.则下列选项不成立的是( )
A.∠D=∠BB.∠E=∠CC.D.
【分析】根据∠DAB=∠CAE,可以得到∠DAE=∠BAC,然后即可判断添加各个选项中的条件是否可以使得△ADE∽△ABC,本题得以解决.
解:∵∠DAB=∠CAE,
∴∠DAB+∠BAE=∠CAE+∠BAE,
∴∠DAE=∠BAC,
∴当添加条件∠D=∠B时,则△ADE∽△ABC,故选项A不符合题意;
当添加条件∠E=∠C时,则△ADE∽△ABC,故选项B不符合题意;
当添加条件时,则△ADE∽△ABC,故选项C不符合题意;
当添加条件时,则△ADE和△ABC不一定相似,故选项D符合题意;
故选:D.
【点评】本题考查相似三角形的判定,解答本题的关键是明确题意,利用三角形相似的判定方法解答.
9.如图,点F是▱ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论正确的有( )
①=;②=;③=;④=.
A.1个B.2个C.3个D.4个
【分析】由四边形ABCD是平行四边形,可得CD∥AB,AD∥BC,CD=AB,AD=BC,然后根据平行线分线段成比例定理,对各个结论进行分析即可求得答案.
解:∵四边形ABCD是平行四边形,
∴CD∥AB,AD∥BC,CD=AB,AD=BC,
∴=,故①正确;
∴=,即=,故②正确;
∴=,故③错误;
∴=,即=,故④正确.
故选:C.
【点评】本题考查平行线分线段成比例定理,用到的知识点:三条平行线截两条直线,所得的对应线段成比例;平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.也考查了平行四边形的性质.
10.如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=9,则EF的长为( )
A.1B.1.5C.3D.4.5
【分析】利用直角三角形斜边上的中线等于斜边的一半,可求出DF的长,再利用三角形的中位线平行于第三边,并且等于第三边的一半,可求出DE的长,进而求出EF的长.
解:∵∠AFB=90°,D为AB的中点,
∴DF=AB=3,
∵DE为△ABC的中位线,
∴DE=BC=4.5,
∴EF=DE﹣DF=1.5,
故选:B.
【点评】本题考查了直角三角形斜边上的中线性质:在直角三角形中,斜边上的中线等于斜边的一半和三角形的中位线性质:三角形的中位线平行于第三边,并且等于第三边的一半.
11.如图,E为▱ABCD的边AB延长线上的一点,且BE:AB=2:3,△BEF的面积为4,则▱ABCD的面积为( )
A.30B.27C.14D.32
【分析】用相似三角形的面积比等于相似比的平方,以及面积的和差求解.
解:∵四边形ABCD是平行四边形,
∴AB=CD,CD∥AB,BC∥AB,
∴△BEF∽△AED,
∵,
∴,
∴,
∵△BEF的面积为4,
∴S△AED=25,
∴S四边形ABFD=S△AED﹣S△BEF=21,
∵AB=CD,,
∴,
∵AB∥CD,
∴△BEF∽△CDF,
∴,
∴S△CDF=9,
∴S平行四边形ABCD=S四边形ABFD+S△CDF=21+9=30,
故选:A.
【点评】此题是相似三角形的性质和判定,主要考查了平行四边形的性质,相似三角形的性质,解本题的关键是掌握相似三角形的面积比等于相似比的平方.
12.下列条件不能判定△ADB∽△ABC的是( )
A.∠ABD=∠ACBB.∠ADB=∠ABCC.AB2=AD•ACD.=
【分析】根据有两个角对应相等的三角形相似,以及根据两边对应成比例且夹角相等的两个三角形相似,分别判断得出即可.
解:A、∵∠ABD=∠ACB,∠A=∠A,∴△ABC∽△ADB,故此选项不合题意;
B、∵∠ADB=∠ABC,∠A=∠A,∴△ABC∽△ADB,故此选项不合题意;
C、∵AB2=AD•AC,∴=,∠A=∠A,△ABC∽△ADB,故此选项不合题意;
D、=不能判定△ADB∽△ABC,故此选项符合题意.
故选:D.
【点评】本题考查了相似三角形的判定,利用了有两个角对应相等的三角形相似,两边对应成比例且夹角相等的两个三角形相似.
二.填空题(每题2分,共12分)
13.若,则= .
【分析】根据比例的基本性质变形,代入求值即可.
解:由可设y=3k,x=7k,k是非零整数,
则.
故答案为:.
【点评】本题主要考查了比例的基本性质,准确利用性质变形是解题的关键.
14.设a为一元二次方程2x2+3x﹣2022=0的一个实数根,则2﹣9a﹣6a2= ﹣6064 .
【分析】根据已知得2a2+3a=2022,再将所求式子变形后整体代入即可.
解:∵a为一元二次方程2x2+3x﹣2022=0的一个实数根,
∴2a2+3a﹣2022=0,
∴2a2+3a=2022,
∴2﹣9a﹣6a2,
=2﹣3(3a+2a2)
=2﹣3×2022
=2﹣6066
=﹣6064,
故答案为:﹣6064.
【点评】本题考查一元二次方程的解及求代数式的值,解题的关键将已知和所求式子适当变形,再应用整体思想解决问题.
15.若双曲线的图象经过第二、四象限,则k的取值范围是 k< .
【分析】由反比例函数图象的位置在第二、四象限,可以得出2k﹣1<0,然后解这个不等式就可以求出k的取值范围.
解:∵双曲线的图象经过第二、四象限,
∴2k﹣1<0,
∴k<,
故答案为:k<.
【点评】本题考查了反比例函数的图象及其性质,一元一次不等式的解法.
16.已知点C是线段AB上的黄金分割点,且AC>BC,如果AB=2cm,那么线段BC的长度为 (3﹣) cm.
【分析】利用黄金分割的定义,进行计算即可解答.
解:∵点C是线段AB上的黄金分割点,且AC>BC,AB=2cm,
∴AC=AB=×2=(﹣1)cm,
∴BC=AB﹣AC=2﹣(﹣1)=(3﹣)cm,
故答案为:(3﹣).
【点评】本题考查了黄金分割,熟练掌握黄金分割的定义是解题的关键.
17.如图,在△ABC中,D为AB边上的一点,要使△ABC∽△AED成立,还需要添加一个条件为 ∠ADE=∠C 或∠AED=∠B或= .
【分析】根据相似三角形对应角相等,可得∠ABC=∠AED,故添加条件∠ABC=∠AED即可求得△ABC∽△AED,即可解题.
解:∵∠ABC=∠AED,∠A=∠A,
∴△ABC∽△AED,
故添加条件∠ABC=∠AED即可求得△ABC∽△AED.
同理可得:∠ADE=∠C 或∠AED=∠B或=可以得出△ABC∽△AED;
故答案为:∠ADE=∠C 或∠AED=∠B或=.
【点评】此题考查了相似三角形对应角相等的性质,相似三角形的证明,添加条件∠ABC=∠AED并求证△ABC∽△AED是解题的关键.
18.如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为 9:16 .
【分析】可证明△DEF∽△BAF,根据相似三角形的面积之比等于相似比的平方即可得出答案.
解:∵四边形ABCD为平行四边形,
∴DC∥AB,
∴△DEF∽△BAF,
∵DE:EC=3:1,
∴DE:DC=3:4,
∴DE:AB=3:4,
∴S△DEF:S△BAF=9:16.
故答案为:9:16.
【点评】本题考查了平行四边形的性质以及相似三角形的判定和性质,注:相似三角形的面积之比等于相似比的平方.
三.解答题
19.解方程:
(1)x2﹣2x=2x+1
(2)2(x﹣3)=3x(x﹣3)
【分析】(1)利用配方法解方程;
(2)先移项得到2(x﹣3)﹣3x(x﹣3)=0,然后利用因式分解法解方程.
解:(1)x2﹣4x=1,
x2﹣4x+4=5,
(x﹣2)2=5,
x﹣2=±,
所以x1=2+,x2=2﹣;
(2)2(x﹣3)﹣3x(x﹣3)=0,
(x﹣3)(2﹣3x)=0,
x﹣3=0或2﹣3x=0,
所以x1=3,x2=.
【点评】本题考查了解一元二次方程﹣因式分解法:因式分解法就是利用因式分解求出方程的解的方法,这种方法简便易用,是解一元二次方程最常用的方法.也考查了配方法解一元二次方程.
20.如图,在矩形ABCD中,M是BC上的一点,连接AM,DE⊥AM于点E.
(1)求证:△ADE∽△MAB;
(2)若,AD=8,BM=3,求EM的长.
【分析】(1)由四边形ABCD是矩形,∠BAD=∠B=∠ADC=90°,则∠DAE=∠AMB=90°﹣∠BAM,由DE⊥AM于点E,得∠AED=∠B=90°,即可证明△ADE∽△MAB;
(2)首先由矩形的性质得到AB=CD,然后根据相似三角形的性质求出AM和AE得出,进而求解.
【解答】(1)证明:∵四边形ABCD是矩形,
∴∠BAD=∠B=∠ADC=90°,
∴∠DAE=∠AMB=90°﹣∠BAM,
∵DE⊥AM于点E,
∴∠AED=∠B=90°,
∴△ADE∽△MAB;
(2)∵四边形ABCD是矩形,
∴AB=CD,
∴,
∵△ADE∽△MAB
∴,即,
解得AM=6,AE=4,
∴EM=AM﹣AE=2.
【点评】此题重点考查矩形的性质、相似三角形的判定与性质,证明三角形相似是解题的关键.
21.如图,一次函数y=kx+b(k≠0)与反比例函数(m≠0,x>0)的图象交于A(1,6),B(3,n)两点,AE⊥x轴于点E,BC⊥x轴于点C.
(1)求反比例函数和一次函数的表达式;
(2)根据图象直接写出kx+b>(x>0)时的x的取值范围;
(3)求△AOB的面积.
【分析】(1)把A(1,6)代入可求出m的值,即可得出反比例函数的解析式,根据A、B两点坐标,把B(3,n)代入可求出n值,利用待定系数法即可得出一次函数解析式;
(2)根据A、B坐标,利用图象找出一次函数图象在反比例函数图形上方时x的取值范围即可得答案;
(3)设直线AB交x轴于D,根据一次函数解析式可求出D点坐标,根据S△AOB=S△AOD﹣S△BOD即可得答案.
解:(1)将A(1,6)代入得m=6,
∴反比例函数为,
把B(3,n)代入的,n=,
∴B(3,2)
将A(1,6)和B(3,2)代入y=kx+b得
解得,
∴一次函数的表达式是y=﹣2x+8.
(2)∵A(1,6),B(3,2)
∴观察图象得:kx+b>(x>0)时的x的取值范围为1<x<3.
(3)设直线AB交x轴于D,
∴y=0时,﹣2x+8=0,
解得:x=4,
∴点D(4,0),
∴S△AOB=S△AOD﹣S△BOD=.
【点评】本题考查反比例函数与一次函数综合、利用图象求不等式的解集,待定系数法求反比例函数及一次函数解析式,分割法求三角形面积,熟练掌握反比例函数图形上点的坐标特征是解题关键.
22.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
【分析】(1)利用对应两角相等,证明两个三角形相似△ADF∽△DEC;
(2)利用△ADF∽△DEC,可以求出线段DE的长度;然后在Rt△ADE中,利用勾股定理求出线段AE的长度.
【解答】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C.
在△ADF与△DEC中,
∴△ADF∽△DEC.
(2)解:∵四边形ABCD是平行四边形,
∴CD=AB=8.
由(1)知△ADF∽△DEC,
∴,
∴DE===12.
∵AD∥BC,AE⊥BC,
∴AE⊥AD,
∴∠EAD=90°,
在Rt△ADE中,由勾股定理得:AE===6.
【点评】本题考查了相似三角形的判定与性质,平行四边形的性质,勾股定理,解决本题的关键是证明△ADF∽△DEC.
23.2022年冬奥会在北京顺利召开,冬奥会吉祥物冰墩墩公仔爆红.据统计冰墩墩公仔在某电商平台1月份的销售量是5万件,3月份的销售量是7.2万件.
(1)若该平台1月份到3月份的月平均增长率都相同,求月平均增长率是多少?
(2)市场调查发现,某一间店铺冰墩墩公仔的进价为每件60元,若售价为每件100元,每天能销售20件,售价每降价1元,每天可多售出2件,为了推广宣传,商家决定降价促销,同时尽量减少库存,若使销售该公仔每天获利1200元,则售价应降低多少元?
【分析】(1)设月平均增长率是x,利用3月份的销售量=1月份的销售量×(1+月平均增长率)2,即可得出关于x的一元二次方程,解之取其正值即可得出结论;
(2)设售价应降低y元,则每件的销售利润为(100﹣y﹣60)元,每天的销售量为(20+2y)件,利用每天销售该公仔获得的利润=每件的销售利润×日销售量,即可得出关于y的一元二次方程,解之即可求出y的值,再结合要尽量减少库存,即可得出售价应降低20元.
解:(1)设月平均增长率是x,
依题意得:5(1+x)2=7.2,
解得:x1=0.2=20%,x2=﹣2.2(不合题意,舍去).
答:月平均增长率是20%.
(2)设售价应降低y元,则每件的销售利润为(100﹣y﹣60)元,每天的销售量为(20+2y)件,
依题意得:(100﹣y﹣60)(20+2y)=1200,
整理得:y2﹣30y+200=0,
解得:y1=10,y2=20.
又∵要尽量减少库存,
∴y=20.
答:售价应降低20元.
【点评】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
24.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他站在距离树12m的地方,调整三角板DEF的位置,设法使斜边DF保持水平,并且直角边DE与树顶点B在同一直线上.已知纸板的两条直角边DE=30cm,EF=20cm,测得斜边DF离地面的高度为1.5m,求树的高度.
【分析】先判定△DEF∽△DCB,然后根据相似三角形对应边成比例列式求出BC的长,再加上AC即可得解.
解:∵∠D=∠D,∠DEF=∠BCD,DE=30cm=0.3m,EF=20cm=0.2m,
∴△DEF∽△DCB,
∴,即,
解得:BC=8(m),
∵AC=1.5m,
∴AB=AC+BC=1.5+8=9.5(m),
即树的高度为9.5m.
【点评】本题考查了相似三角形的应用,主要利用了相似三角形对应边成比例的性质,判定出△DEF∽△DCB是解题的关键.
25.如图,矩形ABCD为台球桌面,AD=260cm,AB=130cm,球目前在E点位置,AE=60cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
【分析】(1)利用“两角法”证得这两个三角形相似;
(2)由(1)中相似三角形的对应边成比例来求线段CF的长度.
【解答】(1)证明:如图,在矩形ABCD中:∠DFC=∠EFB,∠EBF=∠FCD=90°,
∴△BEF∽△CDF;
(2)解:∵由(1)知,△BEF∽△CDF.
∴=,即=,
解得:CF=169.
即:CF的长度是169cm.
【点评】本题考查了相似三角形的应用.此题利用了“相似三角形的对应边成比例”推知所求线段CF与已知线段间的数量关系的.
26.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(1)求证:AC2=AB•AD;
(2)求证:CE∥AD;
(3)若AD=8,AB=12.求EF的长.
【分析】(1)证明△DCA∽△CBA,由相似三角形的性质得出=,即可得出结论;
(2)根据直角三角形斜边中线的性质可知EC=EA=EB,推出∠DAC=∠EAC=∠ACE即可证明;
(3)由AD∥CE,可得==,进而可求出答案.
【解答】(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△DCA∽△CBA,
∴=,
∴AC2=AB•AD.
(2)证明:∵∠ACB=90°,E为AB的中点,
∴CE=AE=EB,
∴∠EAC=∠ECA,
∵∠DAC=∠EAC,
∴∠DAC=∠ECA,
∴AD∥EC.
(3)解:∵AD=8,AB=12,
∴AC2=AB•AD=8×12=96.
∴AC=,
∴CD=,
∵∠ACB=90°,E为AB的中点,
∴CE=AB=6,
∵AD∥CE,
∴∠ADC+∠DCE=180°,
∴∠DCE=90°,
∴DE=,
∵△ECF∽△DAF,
∴===,
∴,
∴.
【点评】此题是四边形综合题,主要考查了直角三角形的性质,角平分线的定义,平行线的判定和性质,勾股定理,相似三角形的判定和性质,熟练掌握相似三角形的判定与性质是解本题的关键.
2023-2024学年广西贵港市覃塘区七年级(上)期末数学试卷(含解析): 这是一份2023-2024学年广西贵港市覃塘区七年级(上)期末数学试卷(含解析),共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年广西贵港市桂平市九年级(上)期末数学试卷(含解析): 这是一份2023-2024学年广西贵港市桂平市九年级(上)期末数学试卷(含解析),共19页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
广西贵港市港北三中学2023-2024学年九上数学期末检测模拟试题含答案: 这是一份广西贵港市港北三中学2023-2024学年九上数学期末检测模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,已知二次函数,下列结论正确的是,下列说法中,不正确的个数是,下列命题中,真命题是等内容,欢迎下载使用。












