天津市滨海新区2023年八年级上学期期中考试数学试题（附答案）

这是一份天津市滨海新区2023年八年级上学期期中考试数学试题（附答案），共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1．下列长度的三条线段能构成三角形的是（ ）
A．2cm，3cm，5cmB．5cm，6cm，11cm
C．3cm，4cm，8cmD．5cm，6cm，10cm
2．在 中，若 ， ，则 的度数为（ ）
A．65°B．70°C．75°D．80°
3．在食品包装、街道、宣传标语上随处可见节能、回收、绿色食品、节水的标志，在下列这些示意图标中，是轴对称图形的是（ ）
A．B．
C．D．
4．已知一个多边形的内角和等于900º，则这个多边形是（ ）
A．五边形B．六边形C．七边形D．八边形
5．如图，为了测量B点到河对面的目标A之间的距离，在B点同侧选择了一点C，测得∠ABC＝75°，∠ACB＝35°，然后在M处立了标杆，使∠CBM＝75°，∠MCB＝35°，得到 MBC≌ ABC，所以测得MB的长就是A，B两点间的距离，这里判定 MBC≌ ABC的理由是（ ）
A．SASB．AAAC．SSSD．ASA
6．如图，△ABC≌△BAD，点A和点B，点C和点D是对应点，如果AB＝8cm，BD＝7cm，AD＝6cm，那么BC的长是（ ）
A．5cmB．6cmC．7cmD．8cm
7．已知且的面积为则边上的高等于（ ）
A．13B．3C．4D．6
8．若一个三角形三个内角度数的比为1:2:3，那么这个三角形是（ ）
A．直角三角形B．锐角三角形C．钝角三角形D．等边三角形
9．如图，△ABC中，∠C=90°，AC=BC，AD平分∠CAB交BC于点D，DE⊥AB，垂足为E，且AB=6cm，则△DEB的周长为（ ）
A．4cmB．6cmC．8cmD．10cm
10．如图， ， ，垂足分别为点 ，点 ， 、 相交于点O， ，则图中全等三角形共有（ ）
A．2对B．3对C．4对D．5对
11．如图，△ABC中，∠ACB=90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处．若∠A=24°，则∠BDC等于（ ）
A．42°B．66°C．69°D．77°
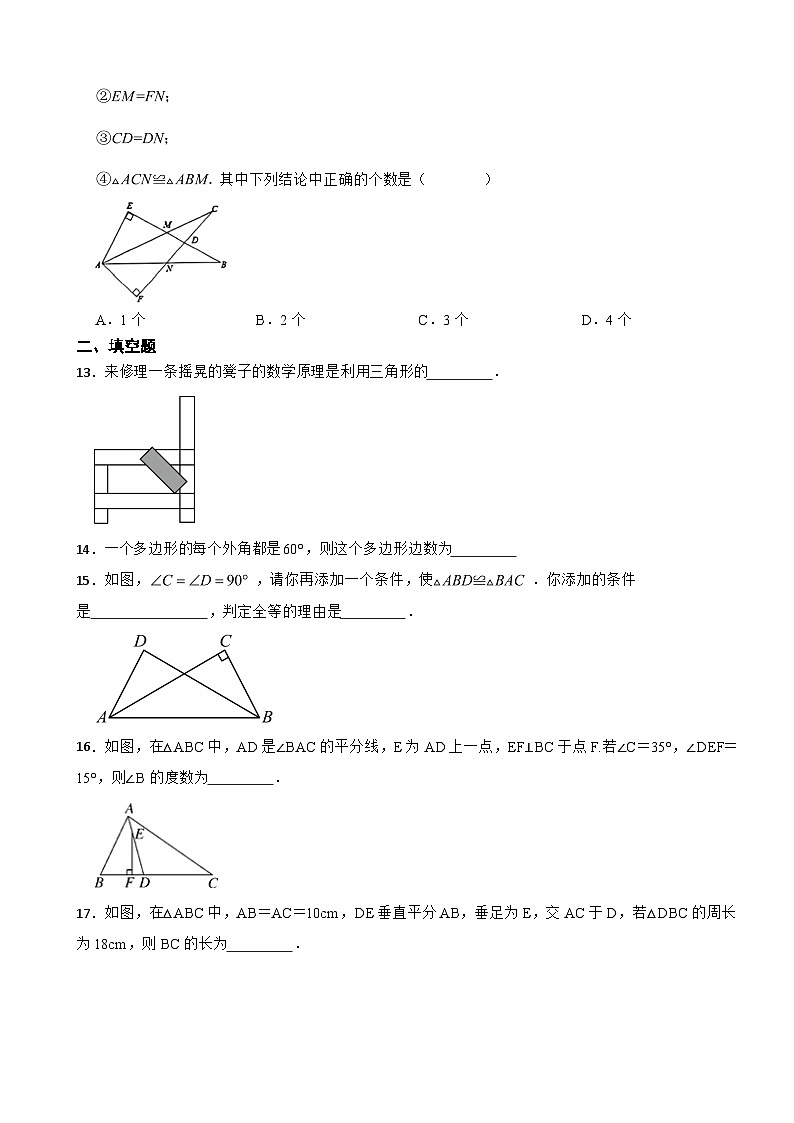
12．如图所示，，下列结论：
其中下列结论中正确的个数是（ ）
A．1个B．2个C．3个D．4个
二、填空题
13．来修理一条摇晃的凳子的数学原理是利用三角形的 ．
14．一个多边形的每个外角都是60°，则这个多边形边数为
15．如图，，请你再添加一个条件，使．你添加的条件是 ，判定全等的理由是 ．
16．如图，在△ABC中，AD是∠BAC的平分线，E为AD上一点，EF⊥BC于点F.若∠C＝35°，∠DEF＝15°，则∠B的度数为 ．
17．如图，在△ABC中，AB＝AC＝10cm，DE垂直平分AB，垂足为E，交AC于D，若△DBC的周长为18cm，则BC的长为 ．
18．如图，已知钝角三角形ABC的面积为20，最长边AB=10，BD平分∠ABC，点M、N分别是BD、BC上的动点，则CM+MN的最小值为 ．
三、解答题
19．如图，AD是△ABC的BC边上的高，AE平分∠BAC，若∠B＝40°，∠C＝72°，求∠AEC和∠DAE的度数．
20．如图，已知，， ，求证：．
21．如图，在△ABC中，∠C=90°，AD平分∠BAC，DE⊥AB，如果DE=5cm，∠CAD=32°，求CD的长度及∠B的度数．
22．如图，在△ABC中，∠ACB＝90°，AC＝BC，BE⊥CE于E，AD⊥CE于D．
（1）求证：△ADC≌△CEB．
（2）AD＝5cm，DE＝3cm，求BE的长度．
23．如图，于点E，于点F．交于点M，求证：．
24．如图所示，已知△ABC中，D为BC上一点，E为△ABC外部一点，DE交AC于一点O，AC=AE，AD=AB，∠BAC=∠DAE．
（1）求证：△ABC≌△ADE；
（2）若∠BAD=20°，求∠CDE的度数．
25．探究：
（1）如图1，在中，平分平分．求证：．
（2）如图2，在中，平分平分外角．猜想和有何数量关系，并证明你的结论．
1．D
2．A
3．B
4．C
5．D
6．B
7．D
8．A
9．B
10．C
11．C
12．C
13．稳定性
14．9
15．；AAS
16．65°
17．8cm
18．4
19．解：∵∠BAC+∠B+∠C=180°，∠B=40°，∠C=72°，
∴∠BAC=68°，
∵AE平分∠BAC，
∴∠BAE=∠CAE=∠BAC=34°，
∴∠AEC=∠B+∠BAE=74°，
∵AD⊥BC，
∴∠ADE=90°，
∴∠DAE=90°-∠AEC=16°．
20．证明： ，，，
在与中有：
，
21．解：∵AD平分∠BAC，DE⊥AB，DC⊥AC，
∴CD=DE=5cm，
又∵AD平分∠BAC，
∴∠BAC=2∠CAD=2×32°=64°，
∴∠B=90°﹣∠BAC=90°﹣64°=26°
22．（1）证明：∵AD⊥CE，∠ACB＝90°，
∴∠ADC＝∠ACB＝90°，
∴∠BCE＝∠CAD（同角的余角相等），
在△ADC与△CEB中
∴△ADC≌△CEB（AAS）；
（2）解：由（1）知，△ADC≌△CEB，
则AD＝CE＝5cm，CD＝BE．
∵CD＝CE﹣DE，
∴BE＝AD﹣DE＝5﹣3＝2（cm），
即BE的长度是2cm．
23．证明：
即
于点E，于点F，
∴和是直角三角形，
在和中，
，
在和中，
，
．
24．（1）证明：在△ABC和△ADE中，
，
∴△ABC≌△ADE（SAS）
（2）解：∵△ABC≌△ADE，∴∠BAC=∠DAE，∠E=∠C，∵∠BAC=∠BAD+∠DAC，∠DAE=∠DAC+∠CAE，∠BAD=20°，
∴∠CAE=∠BAD=20°，
∵∠E=∠C，∠AOE=∠DOC，
∴∠CAE=∠CDE，
∴∠CDE=20°
25．（1）证明：∵中，
又∵平分平分，
，，
，
根据三角形内角和定理可知
（2）解：，理由如下：
∵平分平分外角，
∵是的外角，是的外角，
∴．