2024年高考数学第一轮复习专题12 函数的图象（解析版）

这是一份2024年高考数学第一轮复习专题12 函数的图象（解析版），共35页。

成套的课件成套的教案成套的试题成套的微专题尽在高中数学同步资源大全QQ群552511468也可联系微信fjmath加入百度网盘群4000G一线老师必备资料一键转存自动更新永不过期成套的课件成套的教案成套的试题成套的微专题尽在高中数学同步资源大全QQ群552511468也可联系微信fjmath加入百度网盘群4000G一线老师必备资料一键转存自动更新永不过期 专题12 函数的图象
【题型归纳目录】
题型一：由解析式选图（识图）
题型二：由图象选表达式
题型三：表达式含参数的图象问题
题型四：函数图象应用题
【考点预测】
一、掌握基本初等函数的图像
（1）一次函数；（2）二次函数；（3）反比例函数；（4）指数函数；（5）对数函数；（6）三角函数.
二、函数图像作法
1、直接画
①确定定义域；②化简解析式；③考察性质：奇偶性（或其他对称性）、单调性、周期性、凹凸性；④特殊点、极值点、与横/纵坐标交点；⑤特殊线（对称轴、渐近线等）.
2、图像的变换
（1）平移变换
①函数的图像是把函数的图像沿轴向左平移个单位得到的；
②函数的图像是把函数的图像沿轴向右平移个单位得到的；
③函数的图像是把函数的图像沿轴向上平移个单位得到的；
④函数的图像是把函数的图像沿轴向下平移个单位得到的；
（2）对称变换
①函数与函数的图像关于轴对称；
函数与函数的图像关于轴对称；
函数与函数的图像关于坐标原点对称；
②若函数的图像关于直线对称，则对定义域内的任意都有
或（实质上是图像上关于直线对称的两点连线的中点横坐标为，即为常数）；
若函数的图像关于点对称，则对定义域内的任意都有
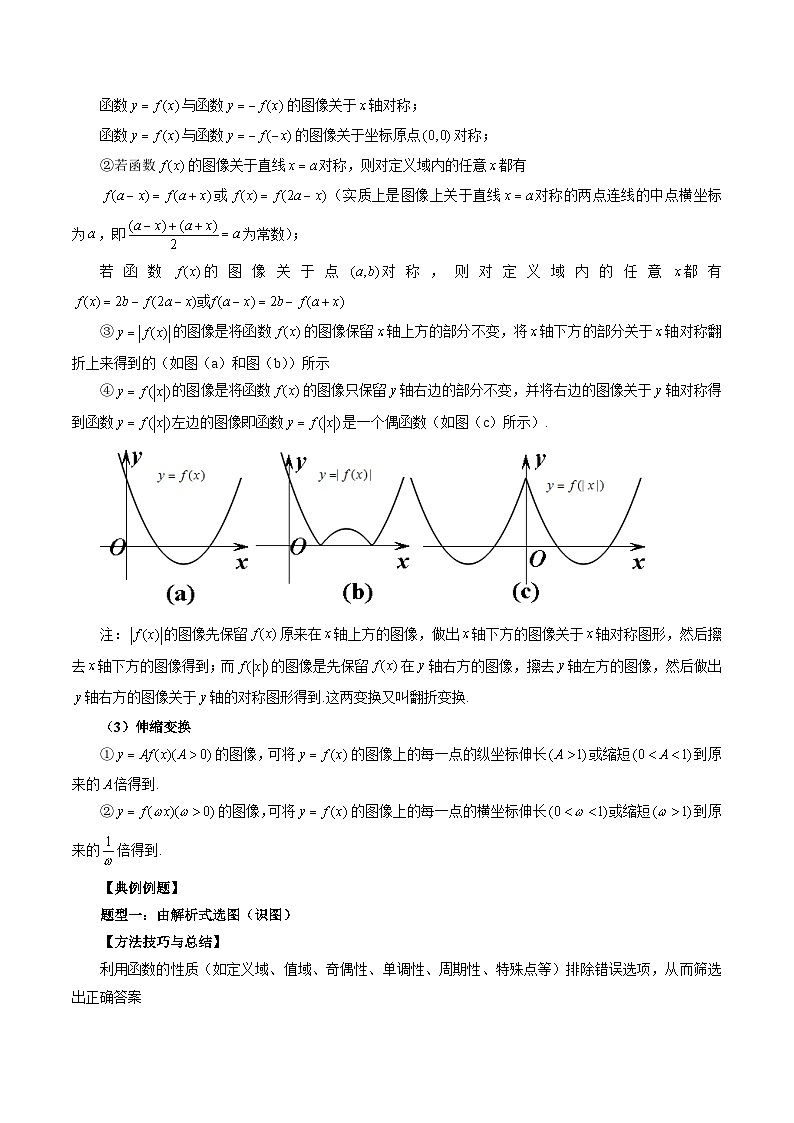
③的图像是将函数的图像保留轴上方的部分不变，将轴下方的部分关于轴对称翻折上来得到的（如图（a）和图（b））所示
④的图像是将函数的图像只保留轴右边的部分不变，并将右边的图像关于轴对称得到函数左边的图像即函数是一个偶函数（如图（c）所示）.

注：的图像先保留原来在轴上方的图像，做出轴下方的图像关于轴对称图形，然后擦去轴下方的图像得到；而的图像是先保留在轴右方的图像，擦去轴左方的图像，然后做出轴右方的图像关于轴的对称图形得到.这两变换又叫翻折变换.
（3）伸缩变换
①的图像，可将的图像上的每一点的纵坐标伸长或缩短到原来的倍得到.
②的图像，可将的图像上的每一点的横坐标伸长或缩短到原来的倍得到.
【典例例题】
题型一：由解析式选图（识图）
【方法技巧与总结】
利用函数的性质（如定义域、值域、奇偶性、单调性、周期性、特殊点等）排除错误选项，从而筛选出正确答案
例1．（2023·四川广安·统考一模）函数在区间上的图象大致为（    ）
A． B．
C． D．
【答案】B
【解析】∵，
∴为奇函数，图象关于原点对称，C、D错误；
又∵若时，，
当时，，当时，，
∴当时，，当时，，A错误，B正确；
故选：B.
例2．（2023·全国·高三专题练习）已知函数则函数的图象是（    ）
A． B． C． D．
【答案】B
【解析】由题意得，当，即时，；
当，即时，
所以
结合函数图象可知：自变量的分界线为，故排除A,C,D
故选：B．
例3．（2023·全国·高三阶段练习）函数在上的大致图象为（    ）
A． B．
C． D．
【答案】C
【解析】∵，∴在上为偶函数．
又，
∴只有选项C的图象符合．
故选：C．
变式1．（2023·全国·高三专题练习）已知函数，则函数的图象是（　　）
A． B．
C． D．
【答案】C
【解析】当时，，故排除A、D选项；当时，，则，排除B选项．
故选：C．
变式2．（2023·全国·高三专题练习）函数在上的大致图象为（    ）
A． B．
C． D．
【答案】C
【解析】由题知的定义域为R，，所以是偶函数，排除A；，排除B，D.
故选：C.
变式3．（2023·全国·高三专题练习）函数的图象大致为（    ）
A． B．
C． D．
【答案】A
【解析】由题可得函数定义域为，且，故函数为奇函数，故排除BD，
由，，故C错误，
故选：A.
变式4．（2023·全国·高三专题练习）函数的图像大致是（    ）
A． B． C． D．
【答案】C
【解析】定义域为，
因为，
所以函数为奇函数，所以排除AB，
当时，，则，
因为当时，，
所以当时，，所以排除D，
故选：C
题型二：由图象选表达式
【方法技巧与总结】
1、从定义域值域判断图像位置；
2、从奇偶性判断对称性；
3、从周期性判断循环往复；
4、从单调性判断变化趋势；
5、从特征点排除错误选项．
例4．（2023·全国·高三专题练习）若函数的图象如图所示，则的解析式可能是（    ）

A． B．
C． D．
【答案】D
【解析】根据函数图象可得函数为偶函数，
A选项，
B选项，所以AB选项为奇函数，
故AB选项不正确；
根据函数图象可得，而C选项，D选项，所以C选项不正确，D选项正确.
故选：D.
例5．（2023·全国·高三专题练习）下图中的函数图象所对应的解析式可能是（    ）

A． B．
C． D．
【答案】A
【解析】根据图象可知，函数关于对称，且当时，，故排除B、D两项；
当时，函数图象单调递增，无限接近于0，对于C项，当时，单调递减，故排除C项.
故选：A.
例6．（2023·全国·高三专题练习）图象为如图的函数可能是（    ）

A． B．
C． D．
【答案】A
【解析】因为为最大值，排除BD；又因为，排除C．
故选：A．
变式5．（2023·全国·高三专题练习）已知函数的图象如图所示，则的解析式可能是（    ）（是自然对数的底数）

A． B．
C． D．
【答案】B
【解析】对于A，函数的定义域为，
由，
所以函数为奇函数，不符合题意；
对于B，函数的定义域为，
由，
所以函数为偶函数，符合题意；
对于C，函数，
则，得且，
故函数的定义域为且，
结合函数图像可知，不符题意；
对于D，函数的定义域为且，
结合函数图像可知，不符题意.
故选：B.
变式6．（2023·全国·高三专题练习）已知某函数的图象如图所示，则该函数的解析式可能为（    ）

A． B． C． D．
【答案】A
【解析】由图象可知，，对选项，当时，函数没有意义，故排除；
由图象可知，，
对：当时，，当时，，满足图象要求；
对：当时，，当时，，不满足图象要求；
故选：.
变式7．（2023·全国·高三专题练习）已知函数，则图象为如图的函数可能是（    ）

A． B．
C． D．
【答案】D
【解析】对于A，，该函数为非奇非偶函数，与函数图象不符，排除A；
对于B，，该函数为非奇非偶函数，与函数图象不符，排除B；
对于C，，则，
当时，，与图象不符，排除C.
故选：D.
变式8．（2023·全国·高三专题练习）已知函数的部分图象如图所示，则函数的解析式可能是（    ）

A． B．
C． D．
【答案】D
【解析】A的函数即为，
当时，，故排除A
由图象可知关于原点对称，则为奇函数，排除B，C.
故选：D.
题型三：表达式含参数的图象问题
【方法技巧与总结】
根据函数的解析式识别函数的图象，其中解答中熟记指数幂的运算性质，二次函数的图象与性质，以及复合函数的单调性的判定方法是解答的关键，着重考查分析问题和解答问题的能力，以及分类讨论思想的应用.
例7．（2023·全国·高三专题练习）已知（且，且），则函数与的图像可能是（    ）
A． B．
C． D．
【答案】B
【解析】由（且，且），
可得，则，则
则，又，则与互为反函数，
则与单调性一致，且两图像关于直线轴对称
故选：B
例8．（2023秋·江西鹰潭·高三贵溪市实验中学校考阶段练习）当时，函数与函数在同一坐标系内的图象可能是（    ）
A． B．
C． D．
【答案】A
【解析】，，是减函数，排除CD，
，，是增函数，又排除B，
故选：A．
例9．（多选题）（2023·全国·高三专题练习）在下列四个图形中，二次函数与指数函数的图象可能是（    ）
A． B．
C． D．
【答案】ABD
【解析】当时，A正确；当时，B正确；
当时，D正确；当时，无此选项．
故选：ABD．
变式9．（多选题）（2023秋·辽宁·高三校联考期中）函数的大致图象可能是（    ）
A． B．
C． D．
【答案】ABD
【解析】由题意知，则，当时，，，，
当时，，，，
所以的大致图象不可能为C，
而当为其他值时，A，B，D均有可能出现，
不妨设，定义域为，此时A选项符合要求；
当时，定义域为，且，
故函数为奇函数，所以B选项符合要求，
当时，定义域为，且，
故函数为偶函数，所以D选项符合要求.
故选：ABD
变式10．（多选题）（2023·全国·高三专题练习）下列可能是函数f（x）＝（其中a，b，c∈）的图象的是（　　）
A． B．
C． D．
【答案】ABC
【解析】A选项中的图象关于y轴对称，B选项中的图象关于原点对称，两个选项均可得函数的定义域为，可得c＝0，又函数f（x）的零点只能由ax＋b产生，所以函数f（x）可能没有零点，也可能零点是x＝，所以AB选项可能符合条件；
而D选项中的图象知函数f（x）的零点在（0，1）内，但此种情况不可能存在，所以D选项不符合条件；
观察C选项中的图象，由定义域猜想c＝1，由图象过原点得b＝0，猜想a＝1，可能符合条件；
故选：ABC
变式11．（多选题）（2023·全国·高三专题练习）函数（其中，）的图象可能是（    ）
A． B．
C． D．
【答案】ABD
【解析】函数的定义域为：，
当时，，选项A符合；
当时，，当时，函数单调递增，
当时，，所以选项D符合；
当时，，当时，，
当时，函数单调递减，所以选项B符合，
故选：ABD
变式12．（多选题）（2023·全国·高三专题练习）已知函数，则的大致图象可能为（    ）
A． B．
C． D．
【答案】ABD
【解析】，即函数是偶函数
当时，函数在区间上单调递减，在区间上单调递增，且，故D正确；
当时，，故A正确；
当时，函数在区间，上单调递减，在区间，上单调递增，且，故B正确；
故选：ABD
变式13．（多选题）（2023·全国·高三专题练习）下列图象中，函数的图象可能是（    ）
A． B．
C． D．
【答案】CD
【解析】，则，故排除AB；
当时，图像关于对称，且当时，在上单调递增，则D有可能；
当时，图像关于对称，且当时，在上单调递减，则C有可能；
故选：CD.
题型四：函数图象应用题
【方法技巧与总结】
函数图象的辨识可从以下方面入手：
(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置．
(2)从函数的单调性，判断图象的变化趋势；
(3)从函数的奇偶性，判断图象的对称性；
(4)从函数的特征点，排除不合要求的图象.
例10．（2023·全国·高三专题练习）列车从地出发直达外的地，途中要经过离地的地，假设列车匀速前进，后从地到达地，则列车与地距离（单位：与行驶时间（单位：）的函数图象为（    ）
A． B．
C． D．
【答案】C
【解析】由题可知列车的运行速度为，
列车到达地的时间为，
故当时，.
故选：C.
例11．（2023·全国·高三专题练习）匀速地向一底面朝上的圆锥形容器注水，则该容器盛水的高度h关于注水时间t的函数图象大致是（    ）
A． B．
C． D．
【答案】A
【解析】设圆锥PO底面圆半径r，高H，注水时间为t时水面与轴PO交于点，水面半径，此时水面高度，如图：

由垂直于圆锥轴的截面性质知，，即，则注入水的体积为，
令水匀速注入的速度为，则注水时间为t时的水的体积为，
于是得，
而都是常数，即是常数，
所以盛水的高度h与注水时间t的函数关系式是，，，函数图象是曲线且是上升的，随t值的增加，函数h值增加的幅度减小，即图象是先陡再缓，
A选项的图象与其图象大致一样，B，C，D三个选项与其图象都不同.
故选：A
例12．（2023秋·甘肃张掖·高三高台县第一中学校考阶段练习）如图，是边长为2的正三角形，记位于直线左侧的图形的面积为，则的函数图象是（    ）.

A． B． C． D．
【答案】A
【解析】根据题意，当时，，
当时，，
当时，，
所以只有A选项符合，
故选：A
变式14．（2023·全国·高三专题练习）下列四个图象中，与所给三个事件吻合最好的顺序为（    ）
①我离开家不久，发现自己把作业本忘在家里了，于是立刻返回家里取了作业本再上学；
②我骑着车一路以常速行驶，只是在途中遇到一次交通堵塞，耽搁了一些时间；
③我出发后，心情轻松，缓缓行进，后来为了赶时间开始加速.

其中y表示离开家的距离，t表示所用时间.
A．④①② B．③①② C．②①④ D．③②①
【答案】A
【解析】对于事件①，中途返回家，离家距离为0，故图像④符合；
对于事件②，堵车中途耽搁了一些时间，中间有段时间离家距离不变，故图像①符合；
对于事件③，前面速度慢，后面赶时间加快速度，故图像②符合；
故选：A.
变式15．（2023·全国·高三专题练习）如图，正△ABC的边长为2，点D为边AB的中点，点P沿着边AC，CB运动到点B，记∠ADP＝x．函数f（x）＝|PB|2﹣|PA|2，则y＝f（x）的图象大致为（　　）

A． B．
C． D．
【答案】A
【解析】根据题意，f（x）＝|PB|2﹣|PA|2，∠ADP＝x．
在区间（0，）上，P在边AC上，|PB|＞|PA|，则f（x）＞0，排除C；
在区间（，π）上，P在边BC上，|PB|＜|PA|，则f（x）＜0，排除B，
又由当x1+x2＝π时，有f（x1）＝﹣f（x2），f（x）的图象关于点（，0）对称，排除D，
故选：A
变式16．（2023·四川泸州·统考模拟预测）如图，一高为H且装满水的鱼缸，其底部装有一排水小孔，当小孔打开时，水从孔中匀速流出，水流完所用时间为若鱼缸水深为h时，水流出所用时间为t，则函数的图象大致是　　

A． B．
C． D．
【答案】B
【解析】函数是关于t的减函数，故排除C，D，
则一开始，h随着时间的变化，而变化变慢，超过一半时，h随着时间的变化，而变化变快，故对应的图象为B，
故选B．
变式17．（多选题）（2023·全国·高三专题练习）如图所示的四个容器高度都相同，将水从容器顶部一个孔中以相同的速度注入其中，注满为止．用下列对应的图象表示该容器中水面的高度h与时间t之间的关系，其中正确的（    ）

A． B．
C． D．
【答案】BCD
【解析】对于A，易知水面高度的增加是均匀的，所以A不正确；
对于B，h 随t的增大而增大，且增大的速度越来越慢，所以B正确；
对于C，h 随t的增大而增大，增大的速度先越来越慢，后越来越快，所以C正确；
对于D，h 随t的增大而增大，增大的速度先越来越快，后越来越慢，所以D正确.
故选：BCD.


【过关测试】
一、单选题
1．（2023·全国·高三对口高考）已知参数方程，t∈[﹣1，1]，以下哪个图符合该方程（　　）
A． B．
C． D．
【答案】B
【解析】利用特殊值法进行排除，
当y＝0时，t＝0，1，﹣1；
当t＝0时，x＝0，当t＝1时，x＝﹣1，当t＝﹣1时，x＝1，
故当y＝0时，x＝0或1或﹣1，即图象经过（﹣1，0），（0，0），（1，0）三个点，
对照四个选项中的图象，只有选项B符合要求．
故选：B．
2．（2023·广东·高三统考学业考试）函数的图象大致为（　　）
A． B．
C． D．
【答案】A
【解析】由对数函数性质知为增函数，故排除BD；
当时，，即函数过点，排除C.
故选：A．
3．（2023·全国·模拟预测）已知函数的定义域为，其图象如图所示，则的解集为（    ）

A． B．
C． D．
【答案】A
【解析】由图可知，当时，，所以；
当时，，所以；
当时，，所以；
故的解集为，
故选：A.
4．（2023·全国·高三专题练习）从函数，，，，中任选两个函数，记为和，若或的图象如图所示，则（    ）

A． B． C． D．
【答案】C
【解析】由图象可知，函数过定点，
当时，，为减函数；
当时，或交替出现.
若，则，不符合题意，故A错误；
若，则，即函数过定点，
又，当时，，不符合题意，故B错误；
若，则，不符合题意，故D错误.
故选：C
5．（2023·全国·高三专题练习）函数的部分图象大致为（    ）
A． B．
C． D．
【答案】C
【解析】由题意可知，函数的定义域为，
因为，
所以为奇函数，图象关于原点对称，排除选项A，B；
当时，，所以，
所以，排除D.
故选：C.
6．（2023·全国·高三专题练习）函数在区间上的图像可能是（    ）
A． B．
C． D．
【答案】A
【解析】当时，，排除C选项；当时，，排除B、D选项.
故选：A.
7．（2023·全国·高三专题练习）已知函数的图像如图所示，则实数a的值可能是（    ）

A． B． C． D．2
【答案】C
【解析】由题意，，故，分子一定有意义.又根据图象可得，当时分式无意义，故此时分母为0，故，即，
故选：C
8．（2023·全国·高三专题练习）函数的大致图象为（    ）
A． B．
C． D．
【答案】C
【解析】函数定义域为，
则，
即为奇函数，函数图象关于原点对称，故排除A、B；
又，故排除D；
故选：C
9．（2023·全国·高三专题练习）已知函数.则当时，的图象不可能是（    ）
A． B．
C． D．
【答案】D
【解析】设，定义域为，
，
所以，为奇函数.
当时，为偶函数，为奇函数.
，，所以选项B可能.
当时，为偶函数，
为奇函数.
，，所以选项A可能.
当时，为偶函数，
为偶函数.
因为，，，所以选项C可能.
故选：D
10．（2023·全国·高三专题练习）下列各个函数图像所对应的函数解析式序号为（    ）

①  ②  ③  ④
A．④②①③ B．②④①③ C．②④③① D．④②③①
【答案】A
【解析】，的定义域为，，的定义域为
在定义域内恒成立，则前两个对应函数分别为④②
当时，则
，令，则
在上单调递增，在上单调递减，则
①对应的为第三个函数
故选：A．
11．（2023·全国·高三专题练习）函数（为常数）的图象一定不可能是（    ）
A． B．
C． D．
【答案】D
【解析】函数的定义域为，由可得.
所以，函数的零点只有一个.
故选：D.
12．（2023秋·贵州遵义·高三统考期中）函数的大致图象为（    ）
A． B．
C． D．
【答案】B
【解析】定义域为，且，
故为偶函数，函数图象关于轴对称，故排除A，
令，即，解得，
又，故排除D，
当时，则，
所以当时，当时，即在上单调递增，在上单调递增，故排除C；
故选：B
13．（2023秋·甘肃张掖·高三高台县第一中学校联考阶段练习）如图是某个函数的图象的一部分，则该函数可能是（    ）

A． B．
C． D．
【答案】B
【解析】对于A,,为偶函数，且，
对于B，，为奇函数，且
对于C,，为偶函数，且，
对于D,,为奇函数，且，
由的图象可知：的图象关于原点对称且过，
故选：B
14．（2023·北京·人大附中校考模拟预测）如图为某无人机飞行时，从某时刻开始15分钟内的速度（单位：米/分钟）与时间（单位：分钟）的关系．若定义“速度差函数”为无人机在时间段内的最大速度与最小速度的差，则的图像为（    ）

A． B．
C． D．
【答案】C
【解析】由题意可得，当时，无人机做匀加速运动，，“速度差函数”；
当时，无人机做匀速运动，，“速度差函数”；
当时，无人机做匀加速运动，，“速度差函数”；
当时，无人机做匀减速运动，“速度差函数”，结合选项C满足“速度差函数”解析式，
故选：C.
15．（2023·河南·校联考一模）已知函数，，，，这四个函数的部分图象如图所示，则函数，，，对应的图象依次是（    ）．

A．①③②④ B．③②①④ C．①④③② D．③④①②
【答案】A
【解析】，
当时，当时恒成立，则在上单调递减；
当时，
当时，，当时，，
则在上单调递增，在单调递减；
故对应得图象为①；
，
当时，当时恒成立，则在上单调递减；
当时，，
当时，，当时，，
则在上单调递增，在单调递减；
故对应得图象为③；
的定义域为R，且，
∴为偶函数，故对应得图象为②；
的定义域为R，且，
∴为奇函数，故对应得图象为④；
故选：A.
二、多选题
16．（2023秋·安徽合肥·高三校考期中）水滴进玻璃容器，如图所示（单位时间内进水量相同），则下列选项匹配正确的是（    ）

A． B． C． D．
【答案】AB
【解析】在a中，容器是圆柱形的，水高度的变化速度应是直线型，与（2）对应，故A正确；在b中，容器下粗上细，水高度的变化先慢后快，与（3）对应，故B正确；在c中，容器为球型，水高度的变化为快—慢—快，与（1）对应，故C错误；在d中，容器上粗下细，水高度的变化为先快后慢，与（4）对应，故D错误.
故选：AB.
17．（2023·全国·高三专题练习）已知函数f（x）的局部图象如图所示，则下列选项中不可能是函数f（x）解析式的是（    ）

A．y＝x2cosx B．y＝xcosx C．y＝x2sinx D．y＝xsinx
【答案】ABCD
【解析】由图象知函数为奇函数，则排除A，D，两个函数为偶函数，
当x＞0时，f（x）＞0，排除B，C，
故ABCD都不成立，
故选：ABCD．
18．（2023秋·湖北襄阳·高三校考阶段练习）函数的图象可能是　　
A． B．
C． D．
【答案】ABD
【解析】根据题意，
当时，，，其图象与选项对应，
当时，，在区间上，，其图象在第一象限先减后增，在区间上，为减函数，其图象与选项对应，
当时，，在区间上，为增函数，在区间上，，其图象在第二象限先减后增，其图象与选项对应，
故选：．
19．（2023·江苏·高三专题练习）已知函数，下列选项中可能是函数图像的是（    ）
A． B． C． D．
【答案】BCD
【解析】当时，函数的图象如图所示：
当时，，
若，则导函数有两个负根，即原函数的两个极值点均为负，不存在满足条件图象；
若，则导函数至多有一个根，即原函数在上递增，图象如图所示：
当时，导函数有两个异号的根，即原函数的两个极值点异号，且函数单调性先递减后递增，图象如图所示，
故不可能是函数图象.
故选：．
三、填空题
20．（2023·全国·高三专题练习）已知幂函数的图象如图所示，则______．（写出一个正确结果即可）

【答案】（答案不唯一）
【解析】由幂函数图象知，函数的定义域是，且在单调递减，于是得幂函数的幂指数为负数，
而函数的图象关于y轴对称，即幂函数是偶函数，则幂函数的幂指数为偶数，
综上得：.
故答案为：