新高考数学之函数专项重点突破 专题12 函数的图象(一)

这是一份新高考数学之函数专项重点突破 专题12 函数的图象(一)，文件包含专题12函数的图象一原卷版docx、专题12函数的图象一解析版docx等2份试卷配套教学资源，其中试卷共39页， 欢迎下载使用。
1、明确模拟练习的目的。不但检测知识的全面性、方法的熟练性和运算的准确性，更是训练书写规范，表述准确的过程。
2、查漏补缺，以“错”纠错。每过一段时间，就把“错题笔记”或标记错题的试卷有侧重的看一下。查漏补缺的过程也就是反思的过程，逐渐实现保强攻弱的目标。
3、严格有规律地进行限时训练。特别是强化对解答选择题、填空题的限时训练，将平时考试当作高考，严格按时完成，并在速度体验中提高正确率。
4、保证常规题型的坚持训练。做到百无一失，对学有余力的学生，可适当拓展高考中难点的训练。
5、注重题后反思总结。出现问题不可怕，可怕的是不知道问题的存在，在复习中出现的问题越多，说明你距离成功越近，及时处理问题，争取“问题不过夜”。
6、重视每次模拟考试的临考前状态的调整及考后心理的调整。以平和的心态面对高考。
专题12 函数的图象(一)
专项突破一 画具体函数图象
1．已知函数
(1)画出函数的图象；(2)求的值；(3)写出函数的单调递增区间.
2．画出下列函数的图象：
（1）；（2），；（3），；
（4），；（5），；（6），.
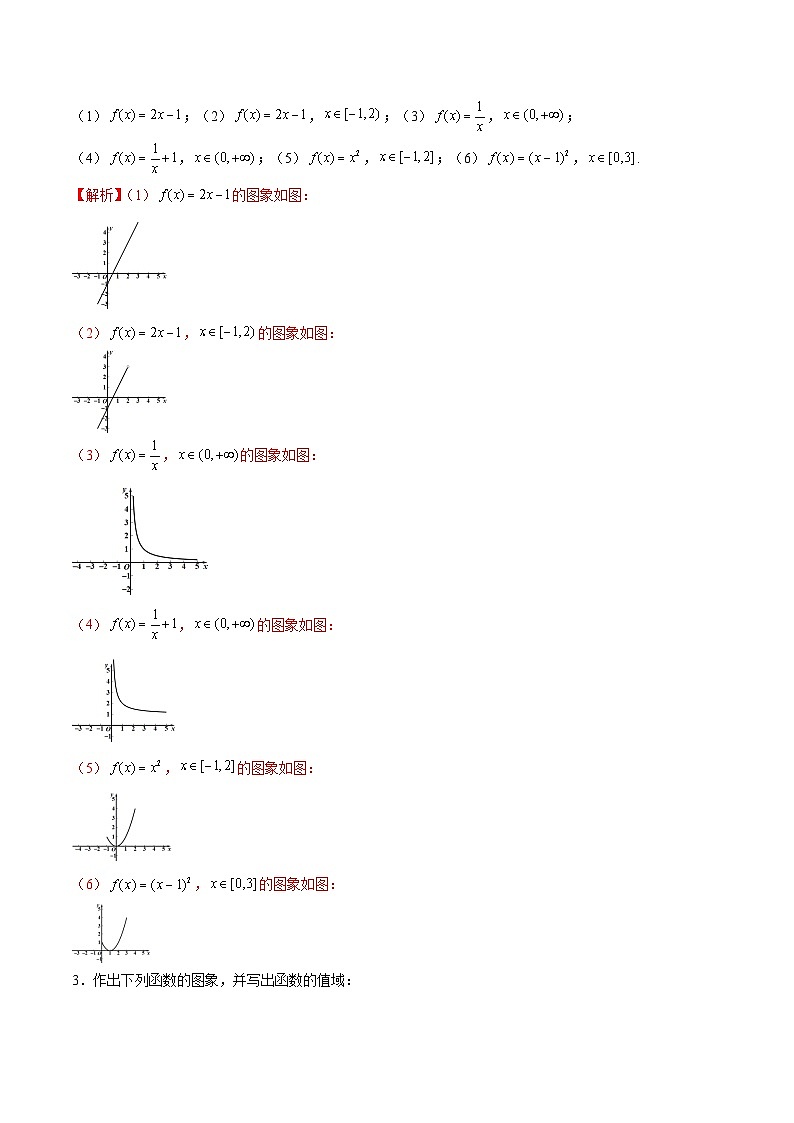
3．作出下列函数的图象，并写出函数的值域：
(1)；(2)．
4．根据的图像，作出下列函数的图像：
(1)；(2)；(3)；(4)．
5．分别画出下列函数的图象：
（1）y＝|lg x|； （2）；（3）y＝x2－2|x|－1; （4）y＝．
6．用“五点法”画出下列函数的简图，并说明这些函数的图象与正(余)弦曲线的区别和联系：
（1） y=csx-1； （2） y=sin.
7．作出函数f(x)＝(x－1)2－1的图象，并分别画出以下函数的图象，
（1）y＝f(x－1); （2）y＝f(x)＋1; （3）y＝－f(x); （4）y＝|f(x)|.
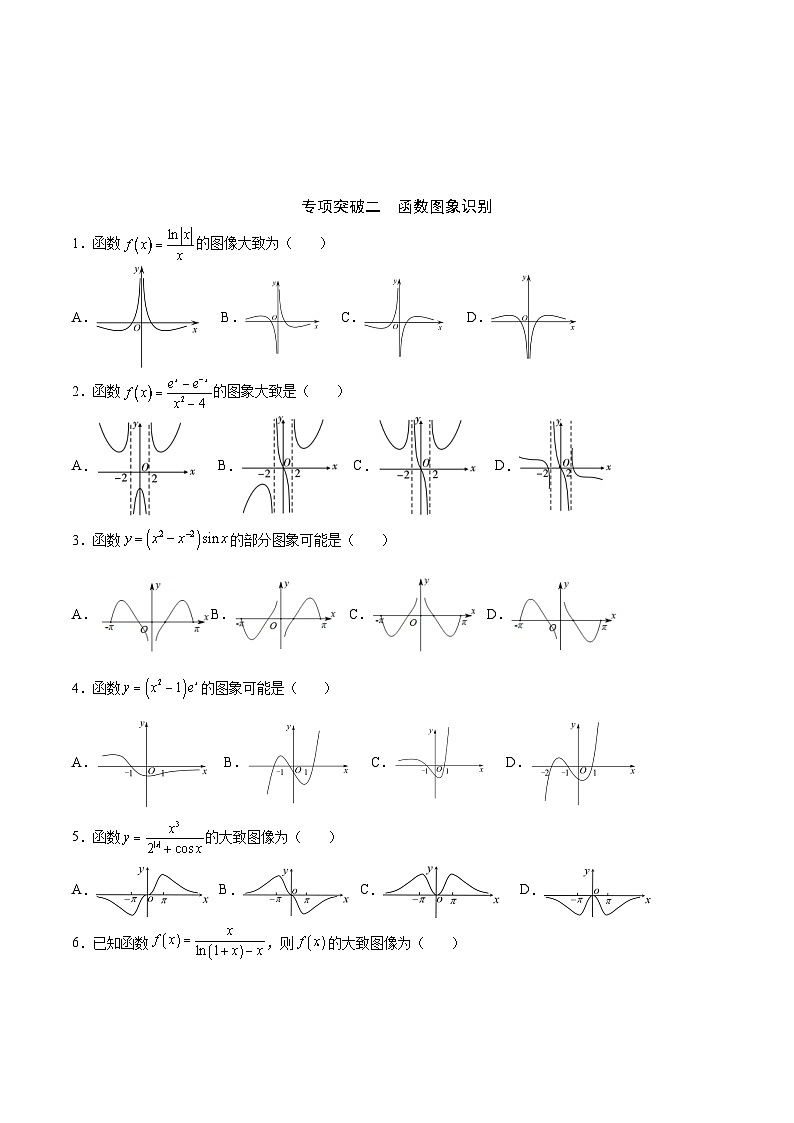
专项突破二 函数图象识别
1．函数的图像大致为（ ）
A． B． C． D．
2．函数的图象大致是（ ）
A． B． C． D．
3．函数的部分图象可能是（ ）
A．B．C．D．
4．函数的图象可能是（ ）
A． B． C． D．
5．函数的大致图像为（ ）
A． B． C．D．
6．已知函数，则的大致图像为（ ）
A． B． C． D．
7．函数与函数且的图象大致是（ ）
A． B． C． D．
8．在同一直角坐标系中，函数与的图像可能是（ ）
A．B．
C．D．
9．已知函数，则函数的大致图象为（ ）
A． B． C． D．
10．函数的图象可能是（ ）
A．B．
C．D．
11．函数的图象可能是（ ）
A． B． C． D．
12．如图所示为函数的图象，则函数的图象可能为（ ）
A． B． C． D．
13．函数，的图象如图所示，则（ ）
A．B．C．D．
14．函数在上的图象大致为（ ）
A．B．
C．D．
15．函数的大致图象是（ ）
A． B． C． D．
16．（多选题）下列可能是函数f（x）＝（其中a，b，c∈）的图象的是（ ）
A． B． C． D．
17．（多选题）函数的图象可能为（ ）
A． B． C． D．
18．下列四个图象中，是函数图象的是________.（填序号）
专项突破三 根据函数图象选择解析式
1．已知函数的部分图象如图所示，则函数的解析式可能是（ ）
A． B． C． D．
2．已知图①中的图象是函数的图象，则图②中的图象对应的函数可能是（ ）
A． B． C． D．
3．已知函数部分图象的大致形状如图所示，则的解析式最可能是（ ）
A． B． C． D．
4．函数的图象如图所示，则函数的解析式为（ ）
A．B．
C．D．
5．函数图象如图，其对应的函数可能是（ ）
A．B．C．D．
6．已知函数的部分图象如图，则的解析式可能是（ ）
A．B．
C．D．
7．已知函数，的图象如图所示，则函数的解析式可能是（ ）
A．B．
C．D．
8．已知函数，，则图象如图的函数可能是( )
A．B．C．D．
9．已知函数的图象如图所示，则此函数可能是（ ）
A．B．
C．D．
10．函数的图象如图，则的解析式可能为（ ）
A．B．
C．D．
11．我国著名数学家华罗庚曾说：“数缺形时少直观，形缺数时难入微，数形结合百般好，隔裂分家万事休．”在数学的学习和研究中，常用函数的图象来研究函数的性质，也常用函数的解析式来研究函数图象的特征．我们从这个商标中抽象出一个如图所示的图象，其对应的函数解析式可能是（ ）
A． B． C． D．
12．如下图，一个“心形”由两个函数的图象构成，则“心形”上部分的函数解析式可能为（ ）
A．B．C．D．
专项突破四 根据实际问题选择函数图像
1．某人去上班，先跑步，后步行.如果y表示该人离单位的距离，x表示出发后的时间，那么下列图象中符合此人走法的是（ ）.
A． B． C． D．
2．如图，在四边形ABCD中，AB∥CD，AB⊥BC，AD＝DC＝2，CB，动点P从点A出发，按照A→D→C→B路径沿边运动，设点P运动的路程为x，△APB的面积为y，则函数y＝f（x）的图象大致是（ ）
A．B．
C．D．
3．如图，一动点从点出发，在直角梯形的一腰和上底上，沿匀速运动，达到点后停止运动．设点运动的时间为，的面积为．则能够反映与之间函数关系的大致图象是（ ）
A．B．C．D．
4．某学生离家去学校，由于怕迟到，一开始就跑步，等跑累了再步行走完余下的路程，若以纵轴表示离家的距离，横轴表示离家后的时间，则下列四个图形中，符合该学生走法的是（ ）
A． B． C． D．
5．点P从O点出发，按逆时针方向沿周长为l的图形运动一周，O､P两点的距离y与点P所走路程x的函数关系如图所示，那么点P所走的图形是（ ）
A． B． C． D．
6．如图，是边长为2的正三角形，记位于直线左侧的图形的面积为，则的函数图象是（ ）.
A． B． C．D．
7．如图，设有圆O和定点C，当从开始在平面上绕O匀速旋转（旋转角度不超过）时，它扫过圆内阴影部分面积S是时间t的函数，它的图像大致是如下哪一种（ ）
A．B．C．D．
8．甲、乙两人沿同一方向前往300米外的目标，甲前150米以2m/s的速度前进，剩下150米以3m/s的速度前进，乙前半段时间以的速度前进，后半段时间以2m/s的速度前进，则以下关于两人去往地的路程与时间函数图象关系中正确的是（ ）
A．B．
C．D．
9．习近平总书记亲自谋划和推动全民健身事业，把全民健身作为全面建成小康社会的重要组成部分，人民的获得感、幸福感、安全感都离不开健康.为响应习总书记的号召，某村准备将一块边长为的正三角形空地（记为）规划为公园，并用一条垂直于边的小路（宽度不计）把空地分为两部分，一部分以绿化为主，一部分以休闲健身为主.如图，轴，小路记为直线，小路右侧为健身休闲区，其面积记为，则函数的图像大致为（ ）
A．B．C．D．
10．如图，扇形的半径，圆心角，是弧上不同于、的动点，过点作于点，作于点，连接，点在线段上，且，设的长为，的面积为，下面表示与的函数关系式的图象可能是（ ）
A． B．C．D．
11．如图，和是两个形状大小完全相同的等腰直角三角形，，点在同一直线上．现从点重合的位置出发，让在直线上向右作匀速运动，而的位置不动．设两个三角形重合部分的面积为，运动的距离为．下面表示与的函数关系式的图象大致是（ ）
A．B．C．D．