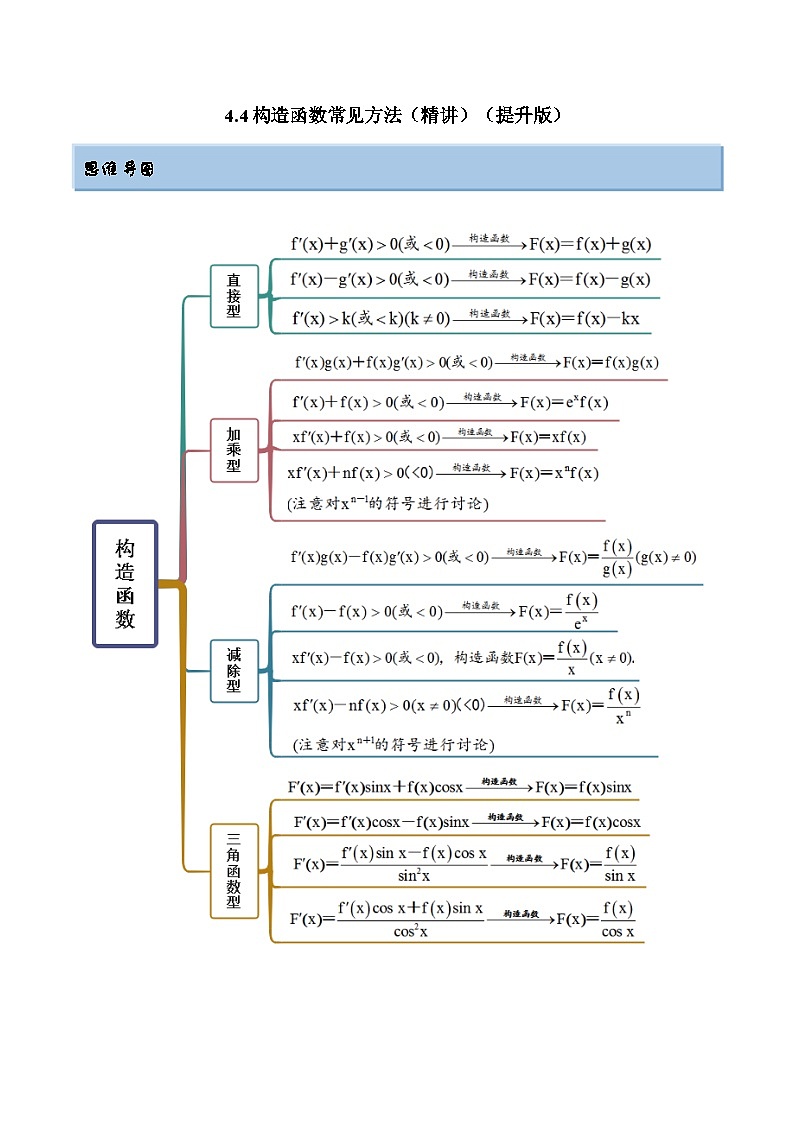
备战高考2024年数学第一轮专题复习4.4 构造函数常见方法（精讲）（提升版）（解析版）

4.4 构造函数常见方法（精讲）（提升版）

考点一 直接型

【例1】（2022·青海玉树）定义在R上的可导函数满足，若，则m的取值范围是（       ）

A． B． C． D．

【答案】B

【解析】令，则，则在R上单减，又等价于，即，由单调性得，解得.故选：B.

【一隅三反】

1．（2021·漠河市高级中学）已知是定义在上的奇函数，是函数的导函数且在上，若，则实数的取值范围为（    ）

A． B．

C． D．

【答案】B

【解析】设，则

又上，，则，即函数在上单调递减，

又是定义在上的奇函数，则函数为上的奇函数，故在上单调递减，

又

，即

可得：，解得：

故选：B.

2（2022年广东潮州）已知是定义在上的奇函数，，当时，，则使得成立的的取值范围是（   ）

A． B．

C． D．

【答案】B

【解析】构造函数，

因为为奇函数，所以=xf(x)=F(x)，所以F(x)为偶函数，

因为当时，，

单调递减，x＞0时，函数F(x)单调递增，

因为f(-1)=0,所以F(-1)=(-1)f(-1)=0.F(1)=0.

因为f(x)＞0，所以，所以，所以x＞1或-1＜x＜0.故选：B

3.（2022·贵州）已知,均是定义在R上的函数，且，当时,，且，则不等式的解集是（   ）

A．(－1，0)∪(1，+∞) B．(－1，0)∪(0，1)

C．(－∞，－1)∪(1，+∞) D．(－∞，－1)∪(0，1)

【答案】D

【解析】，,分别为奇函数偶函数.构造新函数则为奇函数当时，递增.

当时，递增，故答案选D

4．（2022·全国高三）函数是定义在上的函数，且为的导函数，若，则不等式的解集是________．

【答案】

【解析】由题意可知在单调递增，

又，时，时，；

对于，当时，不等式成立，

当时，，不等式不成立；

当时，，且，不等式成立.

综上不等式的解集为.故答案为：

考点二 加乘型

【例2-1】（2022·陕西榆林·三模）已知是定义在上的函数，是的导函数，且，，则下列结论一定成立的是（       ）

A． B． C． D．

【答案】D

【解析】令，则，则是增函数，

故，即，可得.故选：D

【例2-2】（江苏省淮安市2022届高三下学期5月模拟数学试题）已知偶函数的定义域为R，导函数为，若对任意，都有恒成立，则下列结论正确的是（       ）

A． B． C． D．

【答案】C

【解析】令，则，则A错误；

令，则，

当时，由，

，则在上单调递增，

又因为偶函数的定义域为R，

∴为偶函数，在上单调递增，

，，故B错误；

，，故C正确；

由题意，不妨假设(c为常数)符合题意，此时，故D错误.故选：C.

【一隅三反】

1．（2022·河南）已知函数的定义域为，其导函数是，且．若，则不等式的解集是（       ）

A． B．

C． D．

【答案】B

【解析】构造函数，其中，

则，

故函数在上为增函数，且，

因为，由可得，即，解得.故选：B.

2．（2022·辽宁·大连二十四中模拟预测）已知函数，若且，则有（       ）

A．可能是奇函数，也可能是偶函数 B．

C．时， D．

【答案】D

【解析】若是奇函数，则，

又因为，与矛盾，所有函数不可能时奇函数，故A错误；

令，则，

因为，，所以，所以函数为增函数，

所以，即，所以，故B错误；

因为，所以，，所以，

故，即，

所以，故C错误；

有，即，故D正确.故选：D.

3．（2022·河南濮阳）已知函数为定义域在R上的偶函数，且当时，函数满足，，则的解集是（       ）

A． B．

C． D．

【答案】A

【解析】由题可知，当时，．令，则，

，令，，

令，解得．可知函数在上单调递减﹐在上单调递增．

又，所以，，所以函数在上单调递减，

，可化为，又函数关于对称，

故或，所以不等式的解集为．故选：A

考点三 减除型

【例3-1】（浙江省绍兴市新昌中学2022届）若定义在R上的函数的导函数为，且满足

，则不等式的解集为（       ）

A． B．

C． D．

【答案】A

【解析】由题可设，因为，则，

所以函数在R上单调递增，又，不等式可转化为，

∴，所以，解得，

所以不等式的解集为．故选：A.

【例3-2】（山东省泰安肥城市2022届）定义在上的函数的导函数为，且对任意恒成立.若，则不等式的解集为（       ）

A． B．

C． D．

【答案】B

【解析】由，即，

即，即对恒成立，

令，则在上单调递增，

∵，∴，由即，即，

因为在上单调递增，∴故选：B.

【一隅三反】

1．（河南省部分学校2022届）已知是定义在R上的函数的导数，且，则下列不等式一定成立的是（       ）

A． B．

C． D．

【答案】C

【解析】设，则.

因为，所以，则在R上单调递增.

因为，所以，即，

所以，则A错误；

因为，的大小不能确定，所以，的大小不能确定，则B错误；

因为，所以，则，所以，则C正确；

因为，的大小不能确定，所以，不能确定，则D错误.

故选:C

2．（河南省多校联盟2022）已知函数的导函数为，若对任意的，都有，且，则不等式的解集为（       ）

A． B． C． D．

【答案】C

【解析】设函数，

所以，因为，

所以，即，所以在上单调递减，因为，

所以，因为，整理得，

所以，因为在上单调递减，所以.故选：C.

3．（西藏自治区拉萨中学2022届）设函数是奇函数的导函数，，当时，

，则使得成立的的取值范围是（       ）

A． B．

C． D．

【答案】B

【解析】设，则，

∵ 当时，，

当时，，即在上单调递减.

由于是奇函数，所以,是偶函数，所以在上单调递增.

又，所以当或时，；

当或时，.

所以当或时，.故选：B.

考点四 三角函数型

【例4】（2022·湖北）奇函数定义域为，其导函数是.当时，有，则关于x的不等式的解集为（　　）

A．（，π） B．

C． D．

【答案】D

【解析】令，因为当时，有，

所以，当时，，

所以，函数在(内为单调递减函数，

所以，当时，关于的不等式可化为，即，

所以；

当时，，则关于的不等式可化为，即

因为函数为奇函数，故，也即所以，即，

所以，．综上，原不等式的解集.故选：D．

【一隅三反】

1．（2021·江西鹰潭市）已知奇函数的定义域为，其导函数是．当时，，则关于的不等式的解集为（    ）

A． B．

C． D．

【答案】D

【解析】，∴，

∵当时，，∴，

∴在上单调递减，∵是定义在上的奇函数，

故，∴是定义在上的偶函数．

∴在上单调递增．①当时，，

则不等式可转化为，

即，∴，故．

②当时，，

则不等式可转化为，

即，∴，故．

不等式的解集为．

故选：D．

2．（2022·湖北）已知函数满足：，，且.若角满足不等式，则的取值范围是（    ）

A． B． C． D．

【答案】B

【解析】令

因为，

所以为R上的单调减函数，

又因为，

所以，

即，即，

所以函数为奇函数，

故，

即为，

化简得，

即，即，

由单调性有，

解得，

故选:B.

3（2021·全国高三月考）定义在上的连续函数的导函数为，且成立，则下列各式一定成立的是（    ）

A． B．

C． D．

【答案】C

【解析】由题可得，

所以，

设则，

所以在上单调递减，且

由可得，

所以，，所以选项A､B错误，选项C正确.

把代入，可得，所以选项D错误，故选：C.

考点五 题意型

【例5-1】（河南省平顶山市汝州市2022届）设，，，则（       ）

A． B． C． D．

【答案】D

【解析】设，可得，令，解得，

当时，，单调递减；当时，，单调递增，

所以，即，

则，，所以最小，

又由，因为，所以，所以，

综上可得：.故选：D.

【例5-2】（浙江省温州市乐清市知临中学2022届）下列结论正确的是（       ）

A． B．

C． D．

【答案】B

【解析】构造函数，其中，则，

当时，，此时函数单调递增，

当时，，此时函数单调递减，

对于A选项，，则，即，所以，，A错误；

对于B选项，，则，即，所以，B正确；

对于C选项，，则，即，

所以，，所以，，C错误；

对于D选项，，则，即，所以，，D错误.

故选：B.

【一隅三反】

1．（2022·山西·一模（理））设，，，则、、的大小关系是（       ）

A． B．

C． D．

【答案】D

【解析】构造函数，其中，则，

当时，，所以，函数在上单调递增，

因为，则，即，即，

所以，，

因为，故，即，即，

因此，.

故选：D.

2．（2022·全国·高考真题）设，则（       ）

A． B． C． D．

【答案】C

【解析】设，因为，

当时，，当时，

所以函数在单调递减，在上单调递增，

所以，所以，故，即，

所以，所以，故，所以，

故，

设，则,

令，，

当时，，函数单调递减，

当时，，函数单调递增，

又，

所以当时，，

所以当时，，函数单调递增，

所以，即，所以

故选：C.

3．（2022·浙江·乐清市知临中学模拟预测）下列结论正确的是（       ）

A． B．

C． D．

【答案】B

【解析】构造函数，其中，则，

当时，，此时函数单调递增，

当时，，此时函数单调递减，

对于A选项，，则，即，所以，，A错误；

对于B选项，，则，即，所以，B正确；

对于C选项，，则，即，

所以，，所以，，C错误；

对于D选项，，则，即，所以，，D错误.

故选：B.

4．（2022·江西萍乡·三模）设，，，则（       ）

A． B．

C． D．

【答案】D

【解析】令，

，

，可以判断在上单调递增，

所以，

，

所以，

又因为，，

所以，即，所以，

故选：D.