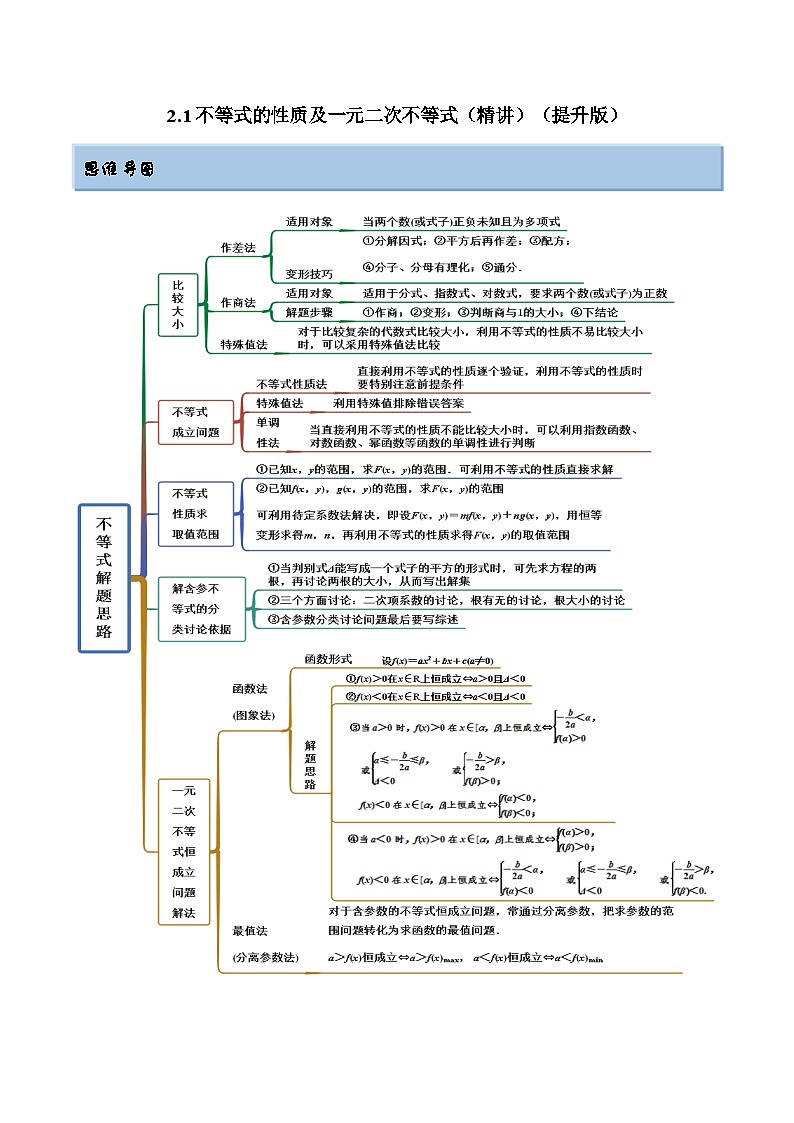
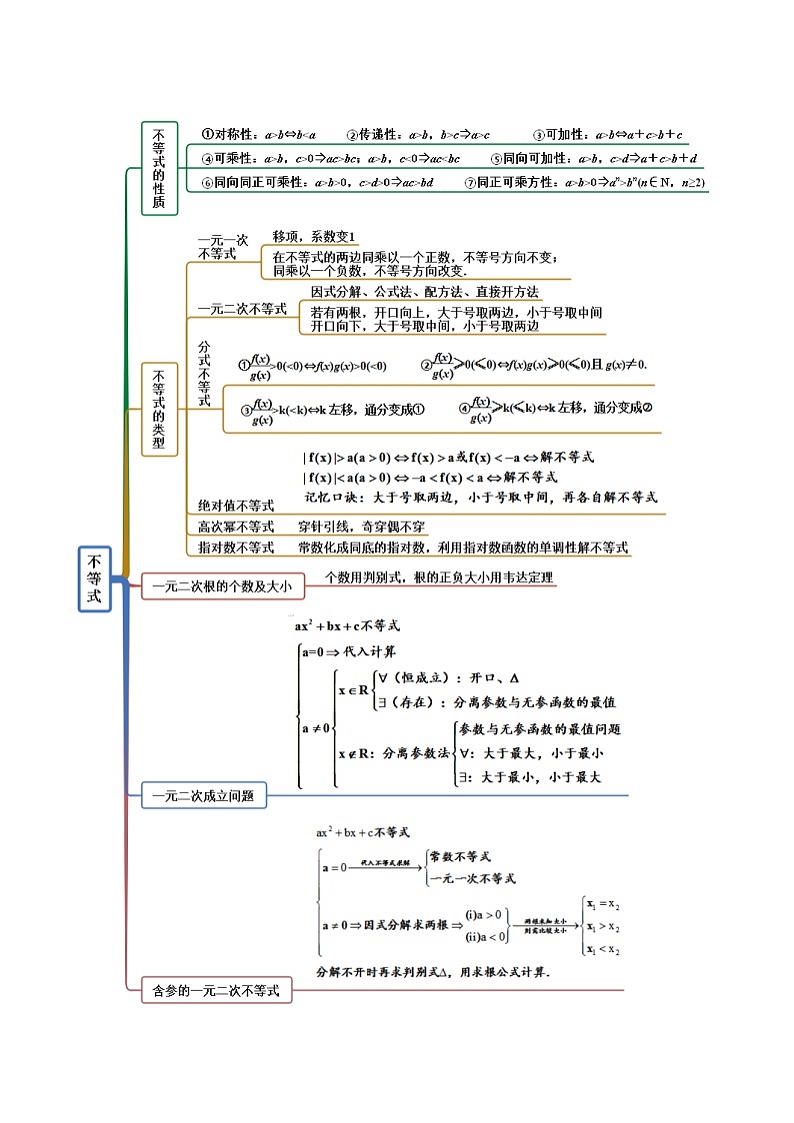
备战高考2024年数学第一轮专题复习2.1 不等式的性质及一元二次不等式（精讲）（提升版）（解析版）

这是一份备战高考2024年数学第一轮专题复习2.1 不等式的性质及一元二次不等式（精讲）（提升版）（解析版），共21页。试卷主要包含了不等式的性质，不等式恒成立，一元二次方程根的分布，比较大小，解含参的一元二次不等式等内容，欢迎下载使用。
2.1 不等式的性质及一元二次不等式（精讲）（提升版）

考点一 不等式的性质【例1-1】（2022·浙江）已知，是正实数，则下列式子中能使恒成立的是（       ）A． B． C． D．【答案】B【解析】对于A，取，该不等式成立，但不满足；对于C，该不等式等价于，取，，该不等式成立，但不满足；对于D，该不等式等价于，取，，该不等式成立，但不满足；下面证明B法一：不等式等价于，而.函数在上单增，故.法二：若，则，故，矛盾.故选：B【例1-2】（2016·浙江）设实数，，满足，，则下列不等式中不成立的是（       ）A． B．C． D．【答案】D【解析】选项A，要证，只需证即可.
由题意可知，则成立，则成立.要证，只需证由题意可知，则，又因为，所以，则，即成立故选项A成立，不符合题意.选项B，要证，只需证即可.由题意可知，则，成立.所以成立，即.要证，只需证，只需证由题意可知，则，，，.所以成立，即成立.故选项B成立，不符合题意.选项C，要证，只需证即可.由题意可知则.又因为，所以.所以成立，即.要证，只需证即可由题意可知则.又因为，所以.所以成立，即成立.故选项C成立，不符合题意.选项D，令，，则
即，所以不成立，符合题意.故选：D【一隅三反】1．（2022·福建·三模）若，则“”的一个必要不充分条件是（       ）A． B． C． D．【答案】B【解析】因为，对于A，当，取，明显可见，不成立，故必要性不成立，A错误；对于B，当，，得，必要性成立；当，取，，明显可见，，则不成立，充分性不成立；则B正确对于C，当，取，明显可见，，则不成立，故必要性不成立，则C错误；对于D，当成立，则，明显可见，成立；当，两边平方，同样有，充分性也成立，D错误；故选：B2．（2022·全国·高三专题练习）若实数，，满足，则下列不等式正确的是（       ）A． B． C． D．【答案】C【解析】实数，，满足，所以对于：当，，时，不成立，故错误；对于：当，，时，，故错误；对于：由于，所以，故，故正确；对于：当，，时，无意义，故错误．故选：．3．（2022·江苏苏州·高三期末）已知 则下列不等式一定成立的是（       ）A． B．
C． D．【答案】C【解析】取，则，故A选项错误；取，，，则B选项错误；取，，则，，即，故D选项错误；关于C选项，先证明一个不等式：，令，，于是时，递增；时，递减；所以时，有极小值，也是最小值，于是，当且仅当取得等号，由，当时，同时取对数可得，，再用替换，得到，当且仅当取得等号，由于，得到，，，即，C选项正确. 故选：C.考点二 不等式恒成立 【例2-1】（2022·海南·嘉积中学）对任意的，恒成立，则的取值范围为（       ）A． B． C． D．【答案】D【解析】当时，由得：，（当且仅当，即时取等号），，解得：，即的取值范围为.选：D.【例2-2】（2022·重庆·高三阶段练习）若关于的不等式对任意恒成立，则实数的取值范围为（       ）A． B． C． D．【答案】A
【解析】令，则.（1）当时，则，令，.故.（2）当时，则，令①当时，，则 ②当时，，则故 （3）当时，则在上恒成立，故.综上所述：故选：A.【一隅三反】1．（2022·全国·高三专题练习）不等式对一切恒成立，则实数的取值范围是（       ）A． B． C． D．【答案】A【解析】令，对一切均大于0恒成立，所以 ，或，或，解得或，，或，综上，实数的取值范围是，或.故选：A.2．（2022·全国·高三专题练习）若不等式的解集为R，则实数的取值范围是（       ）A． B．C． D．【答案】B【解析】∵不等式的解集为R，当a-2＝0，即a＝2时，不等式为3>0恒成立，故a＝2符合题意；当a﹣2≠0，即a≠2时，不等式的解集为R，
则，解得，综合①②可得，实数a的取值范围是．故选：B．3．（2022·浙江·高三专题练习）若不等式对一切恒成立，则的取值范围是（       ）A． B． C． D．【答案】C【解析】若不等式对一切恒成立，则，即，在单调递增，，所以.故选：C4．（2022·全国·高三专题练习）若不等式对任意的恒成立，则（       ）A．， B．，C．， D．，【答案】B【解析】由选项可知，故原不等式等价于，当时，显然不满足题意，故，由二次函数的性质可知，此时必有，即，故选：B考点三 一元二次方程（不等式）根的分布【例3-1】（2022·全国·高三专题练习）关于的一元二次方程：有两个实数根、，则=（       ）A． B． C．4 D．-4【答案】D【解析】由有两个实数根，可得，所以．故选：D．
【例3-2】（2022·浙江·高三专题练习）若不等式的解集中的整数有且仅有1，2，3，则实数的取值范围是___________.【答案】【解析】因为，所以，解得，所以原不等式的解集为，又解集中的整数有且仅有1，2，3，所以解得：，即，故答案为：．【一隅三反】1．（2022·全国·高三专题练习）若和分别是一元二次方程的两根，则的是______.【答案】【解析】由韦达定理：， ，故答案为：.2．（2022·全国·高三专题练习）若关于的不等式的解集中恰有个正整数，则实数的取值范围为______【答案】【解析】解：因为不等式的解集中恰有个正整数，即不等式的解集中恰有个正整数，所以，所以不等式的解集为，所以这三个正整数为，所以，故答案为：.3．（2021·全国·专题练习）已知方程有两个不相等的实数根，且两个实数根都大于2，则实数m的取值范围是（       ）A． B．C． D．【答案】C
【解析】令由题可知：则，即故选：C4．（2021·上海·华师大二附中高一期中）已知实数，关于的不等式的解集为，则实数a、b、、从小到大的排列是(       )A． B．C． D．【答案】A【解析】由题可得：，.由，，设，则.所以，所以，.又，所以，所以.故，.又，故.故选：A.考点四 比较大小【例4-1】（2022·全国·高三专题练习）已知，，，则，，的大小关系为（       ）A． B．C． D．【答案】C【解析】∵，构造函数，，令，则，∴在上单减，∴，故，所以在上单减，∴，
同理可得，故，故选：C.【例4-2】．（2022·广东茂名·高三阶段练习）（多选）已知，，（其中为自然对数的底数），则，，的大小关系为（       ）A． B． C． D．【答案】AD【解析】令，，则，所以当时，当时，所以在上单调递减，在上单调递增，所以，所以，，又，所以，所以；故选：AD【一隅三反】1．（2021·全国·高三专题练习（文））已知，，则（       ）A． B． C． D．【答案】B【解析】因为，，所以，又因为，因为，所以，又因为，所以且，所以，所以，故选：B.2．（2022·山东·模拟预测）已知非零实数m，n满足，则下列关系式一定成立的是（       ）A． B．C． D．【答案】D【解析】因为，所以.取，，得，故A选项不正确；取，，得，所以，故B选项不正确；取，，得
，故C选项不正确；当时，则，所以，所以，当时，则，，所以，当时，，所以，综上得D选项正确，故选：D.3．（2022·广东广州·一模）若正实数a，b满足，且，则下列不等式一定成立的是（       ）A． B． C． D．【答案】D【解析】因为，为单调递增函数，故，由于，故，或，当时，，此时；，故；，；当时，，此时，，故；，；故ABC均错误；D选项，，两边取自然对数，，因为不管，还是，均有，所以，故只需证即可，设（且），则，令（且），则，当时，，当时，，所以，所以在且上恒成立，故（且）单调递减，因为，所以，结论得证，D正确故选：D考点五 解含参的一元二次不等式
【例5】（2022·全国·高三专题练习）解关于的不等式．【答案】答案见解析【解析】若，原不等式等价于－x＋1<0，解得x>1．若，原不等式等价于，解得或x>1．若，原不等式等价于．①当时，，无解； ②当时，，解，得；③当时， ，解，得；综上所述，当时，解集为或；    当时，解集为{x|x>1}；当时，解集为； 当时，解集为；当时，解集为．【一隅三反】1．（2022·全国·高三专题练习）已知关于的不等式：，当时解不等式．【答案】答案不唯一，具体见解析【解析】原不等式可变形为：， 当时，，所以，即原不等式的解集为；当时，，所以，即原不等式的解集为；当时，，令，所以，若时，，所以原不等式的解集为，若时，，所以原不等式的解集为，若时，，所以原不等式的解集为，综上可知：时，原不等式的解集为；时，原不等式的解集为；
时，原不等式的解集为；时，原不等式的解集为．2．（2022·上海·高三专题练习）解关于的不等式：.【答案】答案见解析【解析】当时，不等式化为，解得；当时，不等式化为，解得，或；当时，，不等式化为，解得；当时，不等式化为，此时无解；当时，，不等式化为，解得；综上，时，不等式的解集是；时，不等式的解集是或；时，不等式的解集是；时，不等式无解；时，不等式的解集是.3．（2022·全国·高三专题练习）设函数．（1）若，求不等式的解集；（2）若（1），，求的最小值．【答案】（1）答案不唯一，具体见解析 ；（2） ．【解析】（1）由题意可得，即为，即，当时，，由，解得或；当时，，可得；当时，，由，解得；
当时，，由，解得．综上可得，时，解集为或；时，解集为；时，解集为；时，解集为；（2）由，，可得，，可得，当时，，可得的最小值为，当且仅当，时等号成立；当时，，可得的最小值为，当且仅当，时等号成立．所以的最小值为．