山东省临沂市临沂河东正直实验学校2023-2024学年九年级上学期10月月考数学试题(无答案)

正直实验学校2023-2024学年第一学期

9年级数学月考试卷

总分：120分  考试时间：120分钟  命题人：刘宝生

注意事项：

1．全卷120分，考试时间120分钟．

2．考生领到试卷和答题卡后，请用0.5mm黑色签字笔在试卷和答题卡上填写姓名和座位号，同时把答案写在答题卡上．

3．作答非选择题必须用0.5mm黑色签字笔将答案写在答题卡上的指定区域．

4．考试期间严肃考纪，禁止传夹带、打暗号、交头接耳等违纪行为，凡发现该科目按0分计算．

5．结束后，停止答题，等监考教师收答题卡，核对无误后方可离开．

一、单选题（共36分）

1．（本题3分）关于x的一元二次方程的根的情况为（    ）

A．两个不相等的实数根       B．两个相等的实数根

C．无实数根          D．无法确定

2．（本题3分）将抛物线向右平移1个单位，再向上平移2个单位后所得到的抛物线的解析式为（    ）

A．   B．   C．   D．

3．（本题3分）用配方法解一元二次方程．则方程可变形为（    ）

A．    B．   C．   D．

4．（本题3分）对于二次函数，下列说法不正确的是（    ）

A．当时，y随x的增大而减小     B．开口向下

C．当时，y有最大值3      D．函数图象与x轴交于点和

5．（本题3分）已知一元二次方程有一个根为-1，则k的值为（    ）

A．2     B．-2     C．4     D．-4

6．（本题3分）抛物线的图象如图所示，则下列四组中正确的是（    ）

A．，，       B．，b<0，

C．，，        D．，，

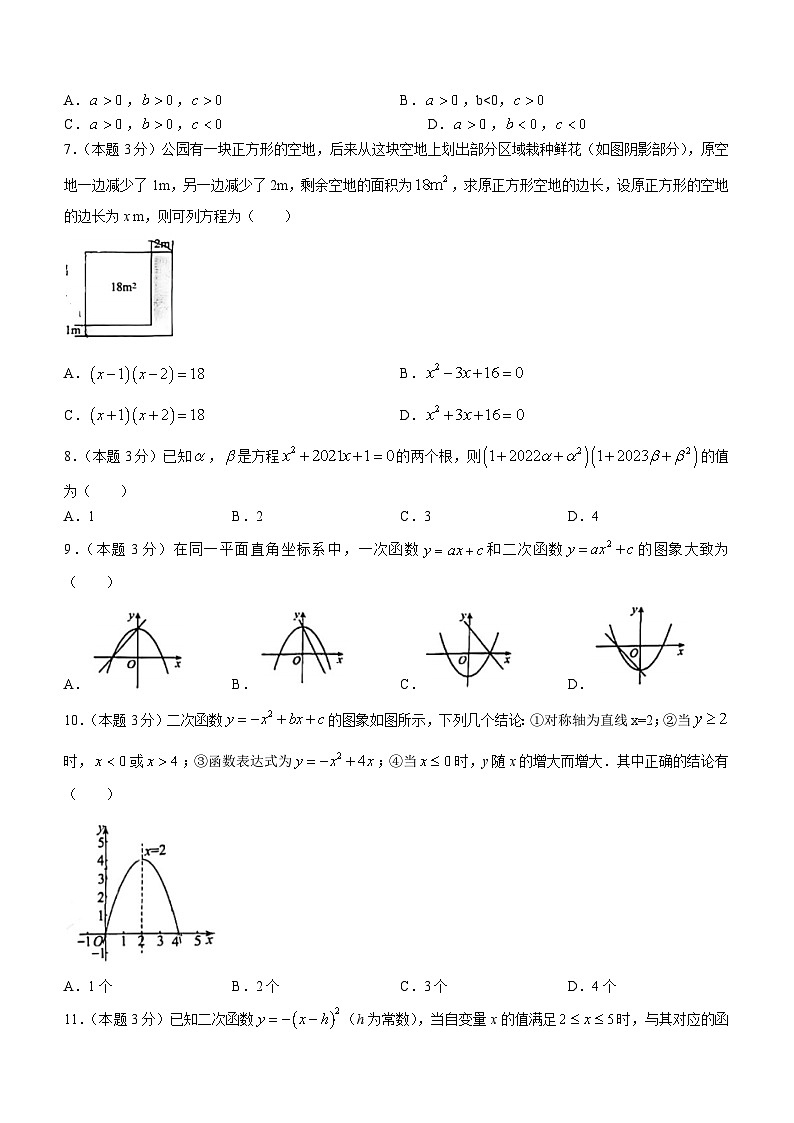
7．（本题3分）公园有一块正方形的空地，后来从这块空地上划出部分区域栽种鲜花（如图阴影部分），原空地一边减少了1m，另一边减少了2m，剩余空地的面积为，求原正方形空地的边长，设原正方形的空地的边长为x m，则可列方程为（    ）

A．        B．

C．        D．

8．（本题3分）已知，是方程的两个根，则的值为（    ）

A．1     B．2     C．3     D．4

9．（本题3分）在同一平面直角坐标系中，一次函数和二次函数的图象大致为（    ）

A．  B．  C．  D．

10．（本题3分）二次函数的图象如图所示，下列几个结论：①对称轴为直线x=2；②当时，或；③函数表达式为；④当时，y随x的增大而增大．其中正确的结论有（    ）

A．1个     B．2个     C．3个     D．4个

11．（本题3分）已知二次函数（h为常数），当自变量x的值满足时，与其对应的函数值y的最大值为-1，则h的值为（    ）

A．3或4    B．1或6    C．1或3    D．4或6

12．（本题3分）已知一元二次方程中，下列说法：①若，则；②若方程两根为-1和2，则；③若方程有两个不相等的实根，则方程必有两个不相等的实根；④若，则方程有两个不相等的实根．其中正确的有（    ）

A．1个     B．2个     C．3个     D．4个

第Ⅱ卷（非选择题）

二、填空题（共16分）

13．（本题4分）抛物线上部分点的横坐标x，纵坐标y的对应值如表所示：

据此我们可以推知一元二次方程的根是______．

14．（本题4分）如果，是方程的两个根，那么______，______．

15．（本题4分）若关于x的方程有实数根，则m的取值范围是______．

16．（本题4分）某商品原售价为100元，连续两次涨价后售价为120元，设两次平均增长率为x，则根据题意可列出方程为______．

三、解答题（共68分）

17．（本题10分）（1）解方程：；

（2）．

18．（本题10分）已知关于x的一元二次方程．

（1）求证：方程有两个不相等的实数根；

（2）如果方程的两实根为，，且，求m的值．

19．（本题8分）已知二次函数，

（1）求证：不论m为何实数，此函数的图象与x轴总有两个交点：

（2）若这个函数图象的对称轴为直线，求这个二次函数的最小值．

20．（本题10分）超市销售某种商品，平均每天可售出20件，每件盈利40元，为扩大销量，增加盈利，该店采取了降价措施．经过一段时间后，发现销售单价每降低1元，平均每天可多售出2件．

（1）若降价6元，则平均每天销售数量为______件；

（2）为尽快减少库存，要使该商店每天销售利润为1200元，每件商品应降价多少元?

21．（本题8分）如图，中，，，，点P从点A开始沿AB边向点B以1cm/s的速度移动，同时点Q从点B开始，沿BC边向点C以2cm/s的速度移动，点Q到达点C后，点P停止运动．

（1）经过t s后，的面积等于，求t的值；

（2）经过t s后，，PQ的长度为5cm，求t的值；

（3）的面积能否等于?

22．（本题10分）如图直线与坐标轴交于点、B，抛物线过点A，B．

（1）求点B的坐标；

（2）求抛物线的解析式；

（3）为线段OA上一动点,过点M作垂直于x轴的直线与直线AB及抛物线分别交于点P，N．求线段PN长度的最大．

23．（本题12分）我们在研究一个新函数时，常常会借助图象研究新函数的性质．在经历列表、描点、连线的步骤后，就可以得到函数图象．利用此方法对函数进行探究．

【绘制图象】

（1）填写下面的表格，并且在平面直角坐标系中描出各点，画出该函数的图象．

【观察探究】

（2）结合图像，写出该函数的一条性质：______．

（3）方程的解是______．

（4）若关于x的方程有两个不相等的实数解，则b的取值范围是______．

【延伸思考】

（5）将该函数的图像经过怎样的变换可以得到函数的图像?写出变换过程，并直接写出当时，自变量x的取值范围．