中职高教版（2021）3.3 抛物线精品课时练习

专题08抛物线

1、抛物线的定义：平面内与一个定点和一条定直线（其中定点不在定直线上）的距离相等的点的轨迹叫做抛物线，定点叫做抛物线的焦点，定直线叫做抛物线的准线．

2、抛物线的数学表达式：(为点到准线的距离).

3、抛物线的标准方程

设，抛物线的标准方程、类型及其几何性质：

4、抛物线的通径(过焦点且垂直于轴的弦)长为.

5、抛物线的焦半径公式如下：（为焦准距）

（1）焦点在轴正半轴，抛物线上任意一点，则；

（2）焦点在轴负半轴，抛物线上任意一点，则；

（3）焦点在轴正半轴，抛物线上任意一点，则；

（4）焦点在轴负半轴，抛物线上任意一点，则.

【题型01抛物线定义的理解】

【题型02利用抛物线定义求方程】

【题型03抛物线上点到定点与焦点距离的和（差）最值】

【题型01抛物线定义的理解】

【典例1】（2023秋·陕西西安·高二统考期末）若抛物线上一点到轴的距离为，则点到抛物线的焦点的距离为        ．

【答案】4

【详解】由题意可得，，P纵坐标为，由其解析式可得P横坐标为，

由抛物线定义知.

故答案为：4

【题型02利用抛物线定义求方程】

【典例1】（2023·全国·高三专题练习）已知动点的坐标满足，则动点的轨迹方程为             ．

【答案】

【详解】设直线，则动点到点的距离为，动点到直线的距离为，又因为，

所以动点M的轨迹是以为焦点，为准线的抛物线，其轨迹方程为．

故答案为：

【题型03抛物线上点到定点与焦点距离的和（差）最值】

【典例1】（2023秋·陕西·高二校联考期末）已知抛物线：的焦点为，抛物线上有一动点，且，则的最小值为（    ）

A．8 B．16 C．11 D．26

【答案】C

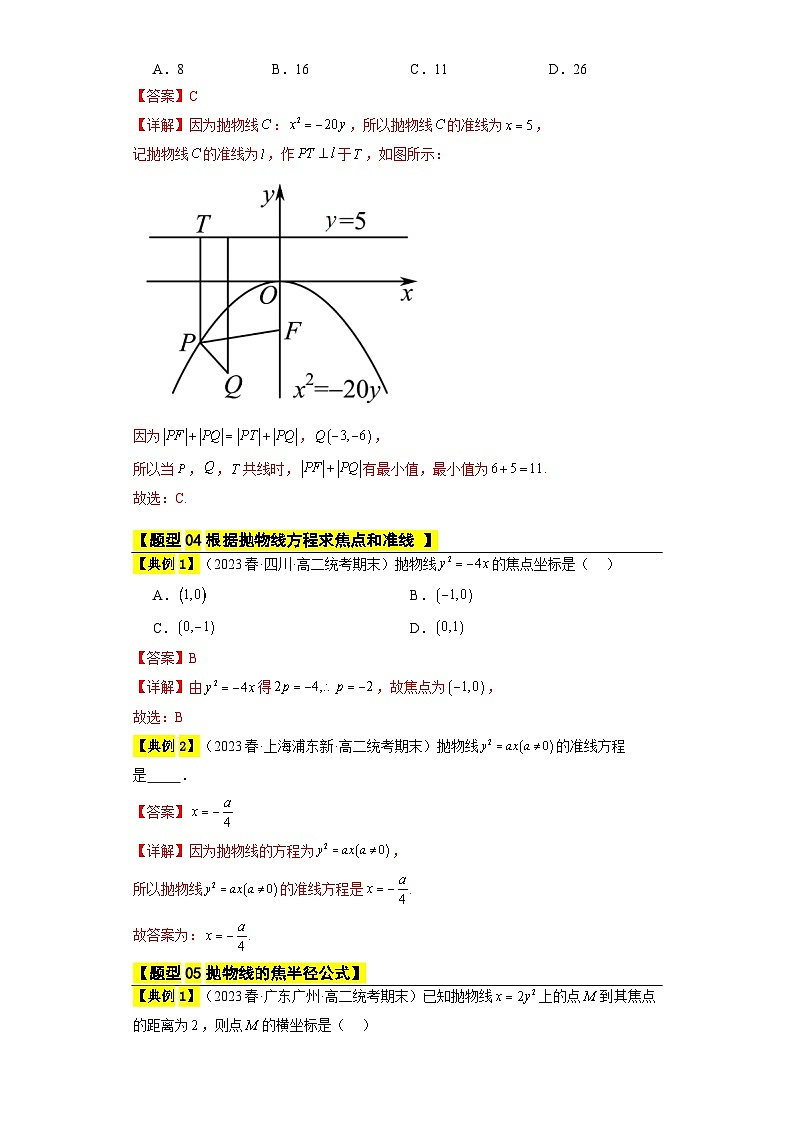
【详解】因为抛物线：，所以抛物线的准线为，

记抛物线的准线为，作于，如图所示：

因为，，

所以当，，共线时，有最小值，最小值为.

故选：C.

【典例1】（2023春·四川·高二统考期末）抛物线的焦点坐标是（    ）

A． B．

C． D．

【答案】B

【详解】由得，故焦点为，

故选：B

【典例2】（2023春·上海浦东新·高二统考期末）抛物线的准线方程是      ．

【答案】

【详解】因为抛物线的方程为，

所以抛物线的准线方程是.

故答案为：.

【题型05抛物线的焦半径公式】

【典例1】（2023春·广东广州·高二统考期末）已知抛物线上的点到其焦点的距离为，则点的横坐标是（    ）

A． B． C． D．

【答案】C

【详解】设点的横坐标为，抛物线的标准方程为，该抛物线的准线方程为，

因为抛物线上的点到其焦点的距离为，则，解得.

故选：C.

【题型06求抛物线方程 】

【典例1】（2023春·四川南充·高二四川省南充高级中学校考期中）准线方程为的抛物线的标准方程是（    ）

A． B．

C． D．

【答案】D

【详解】根据题意，抛物线的准线方程为，

即其焦点在轴负半轴上，且，得，

故其标准方程为：.

故选：D.

【典例2】（2023春·内蒙古呼伦贝尔·高二校考阶段练习）经过点的抛物线的标准方程是（    ）

A．或 B．或

C．或 D．或

【答案】C

【详解】设抛物线的方程为或，

将点代入，可得或，

解得或，

故抛物线的标准方程为或，

故选：C

【题型07直线与抛物线的位置关系】

直线与抛物线的位置关系

设直线:,抛物线:（）,将直线方程与抛物线方程联立整理成关于的方程

(1)若,当时,直线与抛物线相交,有两个交点;

当时,直线与抛物线相切,有一个切点;

当时,直线与抛物线相离,没有公共点.

(2)若,直线与抛物线有一个交点,此时直线平行于抛物线的对称轴或与对称轴重合.因此直线与抛物线有一个公共点是直线与抛物线相切的必要不充分条件.

【典例1】（2023·全国·高三专题练习）直线与抛物线的位置关系为（　　）

A．相交 B．相切 C．相离 D．不能确定

【答案】A

【详解】直线过定点，

∵，

∴在抛物线内部，

∴直线与抛物线相交，

故选：A．

【题型08抛物线的弦长】

过抛物线（）的焦点的一条直线与它交于两点，，则；

【典例1】（2023秋·四川成都·高二校考期末）已知抛物线，其焦点到其准线的距离为，过焦点且倾斜角为的直线交抛物线于两点，

（1）求抛物线的方程及其焦点坐标；

（2）求.

【答案】（1），焦点坐标为；（2）8.

【详解】解：（1）抛物线的焦点到其准线的距离为，得，

所以抛物线的方程为，焦点坐标为.

（2）过焦点且倾斜角为的直线的方程为，设，

联立方程组消去可得，则，

所以.

练 习

一、选择题

1.（2023春·四川广安·高二四川省广安友谊中学校考阶段练习）抛物线C与抛物线关于轴对称，则抛物线C的准线方程是（    ）

A． B． C． D．

【答案】C

【详解】∵抛物线C与抛物线关于轴对称，

∴抛物线C的方程为，

∴抛物线C的准线方程是.

故选：C.

2.（2023·全国·高三专题练习）对抛物线，下列描述正确的是（    ）

A．开口向上，焦点为 B．开口向上，焦点为

C．开口向右，焦点为 D．开口向右，焦点为

【答案】A

【详解】由题知，该抛物线的标准方程为，

则该抛物线开口向上，焦点坐标为.

故选：A.

3.（2023·四川成都·四川省成都列五中学校考三模）若抛物线上的点P到焦点的距离为8，到轴的距离为6，则抛物线的标准方程是（    ）

A． B． C． D．

【答案】C

【详解】由抛物线定义可得：，解得，所以抛物线的标准方程为.

故选：C

4.（2023春·陕西榆林·高二统考期末）已知抛物线的焦点为，点在上，若到直线的距离为7，则          .

【答案】

【详解】由抛物线的焦点为，准线方程为，

因为点在上，且到直线的距离为，

可得到直线的距离为，即点到准线的距离为，

根据抛物线的定义，可得点到焦点的距离等于点到准线的距离，

所以.

故答案为：.

5.（2023·安徽滁州·安徽省定远中学校考二模）已知为抛物线上一点，点到的焦点的距离为，则的焦点坐标为（    ）

A． B． C． D．

【答案】C

【详解】由题意可知，，所以

又知抛物线的准线方程为，

根据抛物线的定义可知，，整理得，解得，

所以的焦点坐标为，

故选：C．

6.（2023·全国·高三专题练习）已知抛物线与直线有且仅有一个交点，则（    ）

A．4 B．2 C．0或4 D．8

【答案】C

【详解】联立得：，

当时，交点为，满足题意；

当时，由，解得，

综上可知： 或，

故选：C

二、填空题

1.（2023秋·广东广州·高二校考期末）已知拋物线的一条切线方程为，则的准线方程为          ．

【答案】

【详解】由，消去得，

由题意，解得，

则抛物线方程为：，

所以抛物线的准线方程为：，即．

故答案为：．

2.（2023秋·高二单元测试）已知抛物线的焦点为F，点M（3，6），点Q在抛物线上，则的最小值为      ．

【答案】

【详解】抛物线的准线方程为，

过作准线的垂线，垂足为，则，

所以.当且仅当与准线垂直时，取等号.

所以的最小值为.

故答案为：.

三、解答题

1.（2023秋·高二课时练习）根据下列条件写出抛物线的标准方程：

（1）焦点是；

（2）准线方程是；

（3）焦点到准线的距离是．

【答案】（1）；（2）；（3）或.

【详解】（1）由题意可知抛物线的焦点在轴的正半轴上，设抛物线的标准方程为，

则，可得，所以，抛物线的标准方程为；

（2）由题意可知抛物线的焦点在轴的正半轴上，设抛物线的标准方程为，

则，可得，因此，抛物线的标准方程为；

（3）抛物线的焦点到准线的距离为，

所以，抛物线的标准方程为或.

2.（2023秋·高二课时练习）直线与抛物线交于两点，求线段AB的长．

【答案】．

【详解】解：抛物线，直线，

将直线方程代入到抛物线方程中，得：，

整理得：，

设，，，，

由一元二次方程根与系数的关系得：，，

所以弦长．

3.（2023春·四川成都·高二成都外国语学校校考阶段练习）已知抛物线的准线方程为.

(1)求的值；

(2)直线交抛物线于、两点，求弦长.

【答案】(1)2；

(2).

【详解】（1）抛物线的准线方程为，依题意，，解得，

所以的值为2.

（2）由（1）知，抛物线，设点，，

由消去y得：，，则，，

所以

.